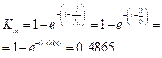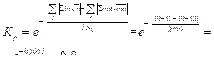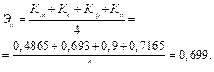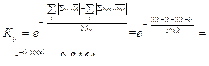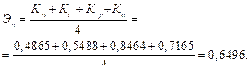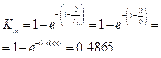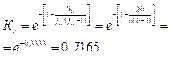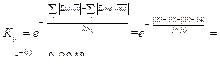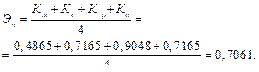Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Особенности функционального моделирования сложных иерархических систем при различных способах организации управления исследуемыми процессами с целью выбора рациональной структуры системы
Аннотация:
Abstract:
| Авторы: Долгов Н.В. (d_n_v92@mail.ru) - Военный институт дополнительного профессионального образования ВУНЦ ВМФ «Военно-морская академия» (адъюнкт), Санкт-Петербург, Россия, Ильин В.А. (komandor.99@mail.ru) - Санкт-Петербургский филиал НИИ «Центрпрограммсистем» (профессор, старший научный сотрудник НИЛ), г. Санкт-Петербург, Россия, доктор военных наук | |
| Количество просмотров: 68 |
Версия для печати |
Введение. Постоянное усложнение систем, искусственных организационно-технических систем в первую очередь, создаваемых человеком в разных областях деятельности, привело не только к осознанию необходимости предвидеть результаты длительных и дорогостоящих работ по созданию таких систем, но и к поиску инструментария для этого. Поиск шел в нап- равлении наработки способности увидеть и оце- нить функционирование разрабатываемой системы раньше, чем она будет создана физически. Целью создания любой системы является ее функционирование. Характер функционирования системы в пределах ее морфологических возможностей определяется управлением работой системы. Именно особенности функционирования системы определяют и ее морфологию, и ее материально-информационные потоки. Известно, что функциональная модель есть графическое представление функционирования систем и объектов [1]. Функциональная модель может использоваться как для анализа процессов протекающих в существующих си- стемах, так и при проектировании новых сис- тем для синтеза их структур [2]. Следует отметить, что анализ функциональных моделей в настоящее время выполняется на качественном уровне путем анализа структуры связей между отдельными функциями моделируемого процесса, сравнения различных структур процесса и процессов между собой. Незначительное количество имеющихся источников и документов по методологии функционального моделирования не приводят методов аналитического количественного анализа функциональных моделей и процессов ими описываемых, а приведенные источники относятся к базовым, что, в свою очередь, подчеркивает актуальность статьи, ее новизну и практическую значимость. Функциональную модель, представленную в нотации технологии IDEF0 [2], можно рассматривать как орграф и, следовательно, анализировать с помощью матрицы смежностей функций процесса между собой [3]. Эффективность процесса (Эп) определяется как среднее арифметическое четырех коэффициентов: масштабного коэффициента процес- са (Kм), оценивающего количество функций в процессе; коэффициента связанности функций процесса (Kс), оценивающего коммуникативность функций в процессе; коэффициента равномерности распределения функций в процес- се (Kр); коэффициента изолированности функций, определяющего общее число несвязанных функций, функций, не имеющих входов или выходов (Kи) [3]. Сложные иерархические системы имеют многоуровневое взаимодействие между ее элементами. Система более высокого уровня выдвигает цель системе более низкого уровня, которая, в свою очередь, выступает как средство для реализации этой цели. Для функционирования системы эти цели и средства их реализации должны быть согласованы между собой [4]. Рассмотрим способы управления сложными системами [5]: Централизованный способ управления обес- печивает использование всех функций и связей между отдельными функциями моделируемого процесса, при использовании единой функции управления на всех уровнях иерархии. Децентрализованное управление предусмат- ривает автономные действия отельных функций без единого управления. Сетецентрическое управление представляет собой матричный информационно-управляющий процесс, в основе которого лежит глобальная информационная взаимосвязь всех функций, интегрированных в единое информационное пространство. Для сетецентрических систем характерна не только вертикальная интеграция между ее процессами, но и широко развитая сеть горизонтальных связей на одном и том же уровне управления между разнородными процессами системы, которые являются источниками и потребителями циркулирующей в системе инфор- мации. Такие системы характеризуются принципами открытости, самоорганизации, слабой иерархии в контуре принятия решений и способностью порождать цели внутри себя [1]. При анализе сложных систем управления промоделируем каждый из способов более подробно. Моделирование процессов сложных систем выполним с использованием метода функционального моделирования [6–8]. Процесс действий сложных систем при централизованном способе управления представлен на рисунке 1 в нотации технологии IDEF0. Процесс включает в себя шесть процедурных функций (А1…А6), выполняющих, например, обработку информации, и одну специфическую функцию управления процессом (А0), связанные между собой прямыми и обратными функциональными связями. Процесс имеет два вхо- да из внешней среды (может быть из другого процесса – Out1, Out2) и два выхода во внешнюю среду (во внешние процессы – In1, In2). Как видим, входы из внешней среды осуществляется через функцию А1, А4, обеспечивающую обработку входной информации и ее передачу другим функциям. Выходы во внешнюю среду осуществляется функциями А3, А6, которые, решают основные задачи процесса, остальные функции выполняют обеспечивающие задачи [9]. Следует заметить, что количество входов и выходов в общем случае может быть любым и определяется только структурой исследуемого процесса [3]. Интерпретируя функциональную модель как орграф, сформируем матрицу связей функций моделируемого процесса (табл. 1). В матрице по строкам единицами и нулями записаны входы в функции, по столбцам соответственно получаем выходы из функций. Суммы входов по строкам и выходов по столбцам позволяют ранжировать функции по степени важности в исследуемом процессе. Общая сумма входов и выходов дает возможность сравнивать структуры одного процесса и разные процессы по их сложности [3]. Таблица 1 Матрица связей функциональной модели действий сложных систем при централизованном способе управления Table 1 Relationship matrix of functional model of complex systems actions under centralized control method
По матрице связей выполним расчет коэффициентов и эффективности процесса.
Общее количество функций fΣ = 6, тогда
Коэффициент связанности функций процесса. Общее число связей, то есть число единиц в матрице SΣ=19, тогда
Коэффициент равномерности распределения функций в процессе. Среднее число входных связей
Коэффициент изолированности функций. Число пустых строк пстр = 0, число пустых столбцов псто = 4, тогда
Эффективность процесса:
Процесс действий сложных систем при децентрализованном способе управления пред- ставлен на рисунке 2 в нотации технологии IDEF0. Он включает в себя шесть процедурных функций (А1…А6), выполняющих обработку информации, связанных между собой прямыми и обратными функциональными связями. Осталь- ные действия выполняются так же, как и при централизованном способе управления. Интерпретируя функциональную модель как орграф, сформируем матрицу связей функций моделируемого процесса (табл. 2). Таблица 2 Матрица связей функциональной модели действий сложных систем при децентрализованном способе управления Table 2 Relationship matrix of the complex systems' functional model of actions under decentralized control method
По матрице связей (табл. 2) выполним расчет коэффициентов и эффективности процесса.
Общее количество функций fΣ = 6, тогда
Коэффициент связанности функций процесса. Общее число связей, то есть число единиц в матрице SΣ=12, тогда
Коэффициент равномерности распределения функций в процессе. Среднее число входных связей
Коэффициент изолированности функций. Число пустых строк пстр = 0, число пустых столбцов псто = 4, тогда
Эффективность процесса:
Процесс действий сложных систем при сетецентрическом способе управления представлен на рисунке 3 в нотации технологии IDEF0. Процесс включает в себя шесть процедурных функций (А1…А6), выполняющих, например, обработку информации, связанных между собой прямыми и обратными функциональными связями. Остальные действия выполняются так же, как и при централизованном способе управ- ления. Интерпретируя функциональную модель как орграф, сформируем матрицу связей функций моделируемого процесса, представленную в таблице 3. Таблица 3 Матрица связей функциональной модели действий сложных систем при сетецентрическом способе управления Table 3 Relationship matrix of the complex systems' functional model of actions under the network-centric management method
Масштабный коэффициент процесса. Общее количество функций fΣ = 6, тогда
Коэффициент связанности функций процесса. Общее число связей, то есть число единиц в матрице SΣ=20, тогда
Коэффициент равномерности распределения функций в процессе. Среднее число входных связей
Коэффициент изолированности функций. Число пустых строк пстр = 0, число пустых столбцов псто = 4, тогда
Эффективность процесса:
Расчет эффективности процессов функциональных моделей действий сложных систем в данном примере при различных способах управления при одинаковом числе функций позволяет сделать вывод, что наиболее эффективным является сетецентрический способ управления.
Заключение
В статье выполнен общий анализ функционального моделирования сложных систем при различных способах управления и выполнен расчет эффективности способов. Предложенный метод позволяет количественно оценить эффективность систем и выбрать наиболее рациональную организацию процессов управления и функционирования сложных систем. Также доказано, что возрастание числа процедурных функций функциональных моделей ведет к уменьшению эффективности процессов, а увеличение прямых и обратных функциональных связей функциональных моделей способствует ее увеличению. Список литературы 1. Черемных С.В., Семенов И.О., Ручкин В.С. Моделирование и анализ систем. IDEF-технологии. М.: Финансы и статистика, 2006. 192 с. 2. Дубейковский В.И. Практика функционального моделирования с AllFusion Process Modeler. М.: Диалог-МИФИ, 2004. 464 с. 3. Ильин В.А., Янча С.П. Методы анализа функциональных моделей // Программные продукты и системы. 2009. Т. 22. № 4. С. 32–34. 4. Шпак В.Ф., Директоров Н.Ф., Мирошников В.И. и др. Информационные технологии в системе управления силами ВМФ. СПб: Элмор, 2005. 827 с. 5. Ильин В.А., Козлов И.Л. К проблеме автоматизации управления силами и средствами, функциональное моделирование // Автоматизация процессов управления. 2009. № 4. С. 53–57. 6. Тебекин А. В. Методология функционального моделирования сложных технических систем модульного типа // Журнал технических исследований. 2021. Т. 7. № 2. С. 3–12. 7. Тебекин А.В., Тебекин П.А., Егорова А.А. Технологические трансформации XXI века как индуцирующий вектор перехода к новому качеству производства // Теоретическая экономика. 2021. № 1. С. 42–53. 8. Тебекин А.В., Петров В.С. Использование методологии моделирования IDEF при формировании структурно-параметрической модели реализации технологий обеспечения эффективного развития промышленных предприятий в условиях постиндустриальной экономики // Транспортное дело России. 2017. № 4. С. 43–49. 9. Харари Ф. Теория графов; [пер. с англ.]. М.: Книжный дом «Либроком», 2009. 296 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=5117&page=article |
Версия для печати |
| Статья опубликована в выпуске журнала № 4 за 2024 год. |
Назад, к списку статей