Рекуррентные нечеткие ситуационно-прецедентные модели для оперативного управления сложными техническими объектами
| Соколов А.М. (ansokol98@mail.ru) - НИУ «МЭИ», Москва, Россия, Аспирант , Борисов В.В. (BYG@yandex.ru) - Смоленский филиал Московского энергетического института (технического университета) (профессор), Смоленск, Россия, доктор технических наук | |
| Ключевые слова: оперативное управление, прецедент, нечеткая ситуационная модель «ситуация–действие», рекуррентная нечеткая ситуационно-прецедентная модель |
|
| Keywords: forecasting time series, precedent, fuzzy situational network of the “Situation-Action” model, recurrent fuzzy situational-precedent model |
|
|
|
|
Введение. В различных отраслях промышленности сложные технические объекты (СТО) используются для решения широкого спектра задач. Эти объекты характеризуются многокомпонентной структурой со сложными взаимосвязями между компонентами, а также большим числом влияющих на их работу внутренних и внешних факторов в условиях неопределенности. Указанные особенности значительно затрудняют, а в ряде случаев делают невозможным построение аналитических моделей, что обусловливает целесообразность использования ситуационных моделей управления. Среди СТО можно выделить отдельный класс специальных роботизированных объектов, предназначенных для решения задач в открытом мире и функционирующих в динамически изменяющихся и неопределенных условиях внешней среды. К таким СТО могут быть отнесены оснащенные манипуляторами и системами технического зрения автономные робототехнические комплексы, обеспечивающие контроль и проведение технологических операций при строительстве и техническом обслуживании, например, в добывающей промышленности, в подводной инфраструктуре, на линиях коммуникаций [1, 2]. Примером таких СТО являются также мобильные роботы, выполняющие исследовательские и разведывательные работы в полевых условиях [3], и снабженные манипуляторами беспилотные аппараты, обслуживающие технику в космическом пространстве [4]. Отличительными особенностями СТО рассматриваемого класса являются сложность прогнозирования ситуаций в процессе эксплуатации объектов, а также большое число опас- ных и аварийных ситуаций, требующих оперативного реагирования [5]. В таких случаях в качестве критерия управления целесообразно рассматривать достижение целевой ситуации за наименьшее число управляющих решений при обеспечении требуемого уровня безопасности. При этом из-за сложности оценки и неопределенности влияния совокупности факторов на результаты управления СТО возможны случаи, когда одинаковым управляющим решениям будут соответствовать различные итоговые ситуации. Таким образом, развитие моделей, способов и алгоритмов для ситуационного управления СТО в условиях неопределенности, учитывающих возможность вариативности результатов применения управляющих решений, является актуальной и практически значимой задачей. Ситуационный подход к управлению СТО в условиях неопределенности Создание адекватных аналитических моделей для управления СТО в условиях неопределенности является нетривиальной и ресурсоемкой задачей, что обосновывает целесообразность применения интеллектуальных моделей, базирующихся на положениях теории нечетких множеств и нечетких вычислений [6]. Одним из современных подходов к решению проблемы учета влияния динамически изменяющихся воздействий внешней среды при управлении СТО является создание интеллектуальных систем на основе комбинирования нечеткой логики и алгоритмов обучения с подкреплением [7, 8]. Данный подход предполагает непрерывную адаптацию в процессе управления СТО с учетом мониторинга их взаимодействия со средой функционирования и закрепления положительного опыта управления [9]. Эвристический характер формирования паттернов управления СТО снижает результативность обучения с подкреплением при наличии аварийных режимов работы и чрезвычайных ситуаций, поскольку при этом цена ошибки значительно возрастает. Для управления СТО в условиях неопределенности распространение получили типы моделей состояний и управления, абстрагирующиеся от внутренней структуры объекта и ориентированные на представление различных ситуаций и/или состояний, а также моделей реализации различных способов переходов между ними, а именно: нечеткие когнитивные модели, нечеткие ситуационно-сетевые модели, нечеткие модели типа «ситуация–действие». Нечеткие когнитивные модели, представляющие СТО в виде множества концептов и нечетких отношений между ними, позволяют при решении задач управления этими объектами осуществлять предварительный анализ СТО [10], вырабатывать рекомендации по их усовершенствованию [11], использовать такие модели СТО в составе более сложных композиционных моделей [12]. Несмотря на наглядность и возможность учета динамики поведения СТО и изменений внешней среды, данный тип моделей затруднительно использовать для ситуационного управления при наличии множества параметров (характеристик) возможных ситуаций. Нечеткие ситуационно-сетевые модели пред- ставляются в виде графа, вершины которого соответствуют нечетким ситуациям, а дуги – управляющим решениям, переводящим СТО из одного состояния в другое. Они предназначены для определения результата применения последовательности управляющих решений, а также стратегии управления, приводящей к требуемой нечеткой ситуации. Авторами работы [13] предложен способ нечеткого ситуационного управления СТО на основе комбинирования нечетких ситуацион- но-сетевых моделей и композиционного гиб- ридного моделирования, применение которого проиллюстрировано на примере моделирования управления центробежными компрессорами. Основным преимуществом данного подхода является возможность формирования наилучших с точки зрения выбранных критериев стратегий управления СТО. К недостаткам метода управления относится то, что учет динамики изменения СТО осуществляется только на уров- не композиционных моделей, но не отражается непосредственно на структуре нечетких ситуационно-сетевых моделей, а также отсутствие в этом методе гибкого механизма адаптации модели к изменяющимся условиям функционирования СТО. Это обусловливает необходимость привлечения дополнительной экспертной информации для построения и актуализации модели. В работе [14] рассмотрены нечеткие ситуационные модели (НСМ) типа «ситуация–действие», которые в явном виде задают соответствия между ситуациями и управляющими решениями, тем самым формируя нечеткую базу знаний. Эти модели ориентированы на определение наиболее близкой эталонной ситуации и на выдачу соответствующего (для ее достижения) управляющего решения, обладают более высоким быстродействием, что определяет целесообразность их применения для оперативного управления СТО в условиях неопределенности. НСМ типа «ситуация–действие» не учитывают различные стратегии управления СТО, что является их основным ограничением. Однако, как отмечалось ранее, при управлении в аварийных и опасных ситуациях, если в качестве критерия эффективности управления рассматривается минимизация количества управляющих решений для достижения целевой ситуации, указанное ограничение не настолько существенно. Отдельным вопросом при постро- ении НСМ типа «ситуация–действие» являются формирование и адаптация нечеткой базы знаний, которая, как правило, задается эксперт- но, что не позволяет в полной мере учитывать влияние динамически изменяющихся факторов внешней среды в условиях неопределенности. Еще одним ограничением этих моделей следует назвать отсутствие учета возможности переходов в различные нечеткие ситуации при применении сходных управляющих воздействий. Как известно, при моделировании функционирования СТО, для которых полное описание невозможно или затруднено из-за структурной и параметрической сложности, а также влияния на их работу стохастических и нестохастических внешних воздействий, применяется прецедентный подход [15–17]. Он предполагает накопление и использование ретроспективной информации о функционировании объекта. В данной статье для повышения эффективности оперативного управления СТО в условиях неопределенности предлагаются новый тип рекуррентных нечетких ситуационно-прецедентных моделей (РНСПМ), а также способ и алгоритмы управления СТО по прецедентам на основе этих моделей. Способ оперативного управления СТО по прецедентам на основе РНСПМ Использование прецедентного подхода для построения и адаптации РНСПМ предполагает создание базы нечетких прецедентов (БНП) для накопления актуальной информации о положительном опыте управления СТО и результатов моделирования. Прецеденты в БНП представляются в виде
где n = 1, …, N – номер прецедента, N – число прецедентов; Каждая нечеткая ситуация S̃i задается набором ситуационных признаков
S̃i = {{μh(pm)/pm}, h = 1, …, H}, m = 1, …, M}, i = 1, …, I, где pm – значение m-го нечеткого ситуационного признака, m = 1, …, M; μh(pm)/pm – значение функции принадлежности признака p̃m к h-му терм-множеству, h = 1, …, H. Оценка степени близости нечетких ситуаций может осуществляться на основе вычисления псевдометрических расстояний, например, нечеткого расстояния Евклида:
при этом ситуации считаются нечетко схожими, если степень нечеткой близости между ними не превышает заданного порога:
Если ситуации являются нечетко схожими, то может быть проведено их объединение:
При достаточном объеме статистических данных возможность перехода СТО из нечеткой ситуации
где Учитывая, что подобные сведения могут быть неопределенными, целесообразно перей- ти к нечеткой оценке возможности перехода из ситуации
где Предлагается способ оперативного управления СТО на основе РНСПМ, заключающийся в рекуррентном поиске прецедентов и применении последовательности соответствующих им управляющих решений для достижения целевой ситуации с использованием наименьшего количества прецедентов:
где Другим условием целесообразности применения способа является достаточно большое число возможных ситуаций и управляющих переходов. Предлагаемый способ оперативного управления СТО по прецедентам на основе РНСПМ включает в себя следующие этапы. Этап 1. Идентификация нечеткой текущей ситуации S̃тек, в которой находится СТО, на основе информации от контрольно-измерительной аппаратуры и датчиков. Этап 2. Задание целевой нечеткой ситуации S̃цел предельного значения dкр для оценки степени сходства между ситуациями. Этап 3. Поиск в БНП прецедента, для которого выполняется следующее условие:
где n – номер прецедента в БНП, n = 1, …, N, N – количество прецедентов в БНП; Этап 4. Итерационный поиск прецедентов и применение соответствующих управляющих решений до достижения S̃цел. При этом на очередной итерации в качестве S̃тек рассматривается конечная ситуация последнего из найденных прецедентов.
На рисунках 3 и 4 проиллюстрирован поиск последовательности прецедентов с наименьшим количеством прецедентных управляющих решений. Предложенный способ может быть применен и для случаев, если критерием эффективности управления СТО является минимизация числа управляющих решений для перехода в целевую ситуацию без учета сопутствующих затрат, например, при игнорировании переходов СТО через промежуточные нежелательные ситуации, соответствующие аварийным режимам работы. Отдельно следует рассмотреть случай, когда имеются прецеденты, у которых начальные ситуации и управляющие решения близки, а конечные ситуации различны. Далее будем называть такие прецеденты связанными. Выбор и применение одного из связанных прецедентов не исключает возможности перехода СТО в незапланированные или даже нежелательные ситуации. Пример подобной ситуации приведен на рисунке 5. Предположим, установлено, что при воздействии одного и того же управляющего решения R̃n или группы схожих управляющих решений {R̃n,h}, где R̃n,1 ≌ R̃n,2 ≌ … ≌ R̃n,H, возможны переходы из ситуации S̃n сразу в несколько ситуаций {S̃h}, h = 1, …, H. Считаем, что переход в незапланированную ситуацию (если она не является нежелательной) будет допустимым, тогда расстояние для всей группы связанных прецедентов может быть определено с использованием выражения
Выражение (6) является обобщением выражения (5), которое используется для случая несвязанных прецедентов.
Для повышения оперативности реагирования СТО на аварийные и опасные ситуации значения ситуационных признаков целевой ситуации S̃цел и предельное значение dкр могут быть заранее согласованы в соответствии с требованиями к обеспечению безопасности СТО (см. 2-й этап способа). Также может быть определено множество допустимых целевых ситуаций, в которые возможен перевод СТО при возникновении аварийных и опасных ситуаций:
где l = 1, …, L, L – число допустимых целевых ситуаций. Особенностью данного варианта является то, что выбор предпочтительной целевой ситуации будет выполняться не на основе выбранного критерия эффективности управления СТО, а на результатах оценки степени ее бли- зости к текущей ситуации. С учетом этого на первом этапе способа дополнительно может осуществляться выбор допустимой целевой ситуации, наиболее близкой к текущей S̃тек:
Применение предложенного способа управления СТО с определением набора допустимых целевых ситуаций целесообразно также, если в качестве нечетких ситуационных признаков, помимо показателей самих СТО, используются параметры, существенно зависящие от динамически изменяющихся факторов внешней среды. Алгоритмическая и программная реализация На рисунке 8 приведена блок-схема алгоритма предложенного способа оперативного управления СТО по прецедентам на основе РНСПМ с критерием эффективности управления, заключающимся в минимизации числа управляющих решений для достижения целевой ситуации. Исходными данными алгоритма является информация о нечеткой текущей ситуации В блоке 4 алгоритма в качестве начальной устанавливается текущая нечеткая ситуация. Далее последовательно для каждого прецедента В блоке 13 рассчитывается скорректированное значение D с учетом риска перехода в незапланированные ситуации на основе обобщенной формулы (6), при этом, если связанные прецеденты не были найдены, возможность перехода устанавливается равной единице. Если полученное значение D является минимальным, информация об управляющем решении и конечной ситуации данного прецедента сохраняется. После рассмотрения всех прецедентов в БНП и определения наилучшего управляющего решения последнее включается в искомую последовательность. Затем осуществляется проверка достижения целевой ситуации (блок 19) в соответствии с выражением Для проверки адекватности и оценки эффективности предложенных РНСПМ и способа управления СТО по прецедентам разработаны программные средства, включающие в себя прог- раммные модули формирования БНП и прецедентного управления. Реализация программных средств выполнена на языке Python 3.12.1, сильной стороной которого является гибкий механизм реализации объектно-ориентированного подхода к на- писанию кода, что позволяет значительно уп- ростить процесс проектирования и поддержки сложных программных систем. Также важным преимуществом языка Python является наличие большого числа сторонних расширений и библиотек с открытым исходным кодом для решения широкого класса задач. Для осуществления математических операций с аппаратом нечеткой арифметики разработано собственное решение на основе библиотеки NumPy, предоставляющей поддержку векторных и матричных операций, а также возможность работы с многомерными массивами данных. Указанная библиотека реализована на языке C, что позволяет повысить скорость вычислений. Для формирования и администрирования БНП, взаимодействия с программными модулями, обмена данными применялась объектно-реляционная СУБД PostgreSQL. Результаты вычислительных экспериментов
В таблице приведены результаты сравнительного анализа применения предложенной РНСПМ и экспертной НСМ типа «ситуация–действие» для различных вариантов начальной ситуации. Доля успешных захватов детали последовательного робота-манипулятора, % Percentage of successful a detail by a robot-manipulator, %
Из таблицы видно, что РНСПМ обеспечивает более высокую долю успешных захватов последовательного робота-манипулятора в усло- виях неопределенности и при возможности различной реакции СТО на одинаковые управляющие воздействия.
На основании проведенных экспериментов можно сделать вывод, что использование разработанных РНСПМ и способа управления СТО по прецедентам на базе этих моделей обеспечивает повышение эффективности управ- ления последовательным роботом-манипулятором и при превышении определенного числа сформированных прецедентов (на рисунке 9 этому значению соответствуют 643 прецедента) обеспечивает лучшие результаты по сравнению с аналогом. Заключение Для повышения эффективности оперативного управления СТО в условиях неопреде- ленности предлагаются новый тип РНСПМ, а также способ и алгоритмы управления СТО по прецедентам на основе таких моделей. Предложенный способ оперативного управления СТО по прецедентам отличается использованием итерационной процедуры поиска последовательности прецедентных управляющих решений. Он также обеспечивает повышение эффективности функционирования СТО при условии адаптации к изменению внутренних и внешних факторов. Разработаны алгоритмические и програм-мные средства, реализующие предложенные модели, способ и алгоритмы управления СТО. В результате вычислительных экспериментов (на примере управления последовательным роботом-манипулятором) подтверждена адекватность предложенных моделей и выполнена оценка эффективности оперативного управления СТО по прецедентам с использованием созданных моделей, способа и алгоритмов в усло- виях неопределенности по сравнению с экспертной нечеткой ситуационной моделью типа «ситуация–действие». Список литературы 1. Филаретов В.Ф., Климчик А.С., Юхимец Д.А., Коноплин А.Ю., Зуев А.В. Интеллектуальные подводные робототехнические комплексы для выполнения осмотровых и технологических операций на морских газопроводах и добычных комплексах // Газовая промышленность. 2020. № 8. С. 30–38. 2. Балабанов А.Н., Безуглая А.Е., Шушляпин Е.А. Управление манипулятором подводного робота // Информатика и автоматизация. 2021. Т. 20. № 6. С. 1307–1332. doi: 10.15622/ia.20.6.5. 3. Тимофеев А.Н., Ракшин Е.А., Заруцкий Н.В. Робототехническая система для ремонта и мониторинга труднодоступного оборудования // Наука и бизнес: пути развития. 2022. № 4. С. 193–196. 4. Мещанов А.С., Губаева Э.И. Управление манипуляторами летательных аппаратов на скользящих режимах при инерционности приводов и неинвариантности к возмущениям // Вестн. Технологического университета. 2020. Т. 23. № 7. С. 100–108. 5. Косицын А.А., Богомолов А.С., Кушников В.А. Задача снижения вероятности развития аварийных комбинаций событий в беспилотных авиационных системах // Прикладная информатика. 2024. Т. 19. № 4. С. 18–34. doi: 10.37791/2687-0649-2024-19-4-18-34. 6. Игнатьев В.В. Компенсация разных типов неопределенностей при управлении техническим объектом с помощью интеллектуальных регуляторов // Программные продукты и системы. 2023. Т. 36. № 3. С. 423–431.doi: 10.15827/0236-235X.143.423-431. 7. Еремеев А.П., Сергеев М.Д., Петров В.С. Интеграция методов обучения с подкреплением и нечеткой логики для интеллектуальных систем реального времени // Программные продукты и системы. 2023. Т. 36. № 4. С. 600–606. doi: 10.15827/0236-235X.144.600-606. 8. Goharimanesh M., Mehrkish A., Janabi-Sharifi F. A fuzzy reinforcement learning approach for continuum robot control. J. of Intelligent & Robotic Systems, 2020, vol. 100, pp. 809–826. doi: 10.1007/s10846-020-01237-6. 9. Пучков А.Ю., Дли М.И., Тиндова М.Г. Метод решения обратной задачи кинематики на основе обучения с подкреплением при управлении роботами-манипуляторами // Прикладная информатика. 2023. Т. 18. № 6. С. 120–133. 10. Борисов В.В. Нечеткие когнитивные модели как основа для исследования сложных систем и процессов // Речевые технологии. 2020. № 1-2. С. 48–62. doi: 10.58633/2305-8129_2020_1-2_48. 11. Chen C.-T., Chiu Y.-T. A study of dynamic fuzzy cognitive map model with group consensus based on linguistic variables. Technological Forecasting and Social Change, 2021, vol. 171, art. 120948. doi: 10.1016/j.techfore.2021.120948. 12. Nair A., Reckien D., van Maarseveen M.F.A.M. A generalised fuzzy cognitive mapping approach for modelling complex systems. Applied Soft Computing, 2019, vol. 84, art. 105754. doi: 10.1016/j.asoc.2019.105754. 13. Борисов В.В., Авраменко Д.Ю. Нечеткое ситуационное управление сложными системами на основе их композиционного гибридного моделирования // Системы управления, связи и безопасности. 2021. № 3. С. 207–237. 14. Starodubtsev M., Bilousov M., Kamardin S., Makarenko H., Shybanov S. Models of technological processes management under conditions of uncertainty. J. of Natural Sci. and Tech., 2024, vol. 3, no. 1, pp. 254–258. 15. Добрынин А.С., Гудков М.Ю., Койнов Р.С. Прецедентный подход к управлению инцидентами в автоматизированных системах управления технологическими процессами // Программные системы и вычислительные методы. 2020. № 2. С. 45–52. doi: 10.7256/2454-0714.2020.2.31040. 16. Черновалова М.В. Нечеткие прецедентные модели для управления проектами с использованием мультионтологического подхода // Прикладная информатика. 2021. Т. 16. № 2. С. 4–16. doi: 10.37791/2687-0649-2021-16-2-4-16. 17. Дли М.И., Черновалова М.В., Соколов А.М., Моргунова Э.В. Нечеткая динамическая онтологическая модель для поддержки принятия решений по управлению энергоемкими системами на основе прецедентов // Прикладная информатика. 2023. Т. 18. № 5. С. 59–76. doi: 10.37791/2687-0649-2023-18-5-59-76. 18. Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. М.: Наука, 1990. 272 с. 19. Борисов В.В., Соколов А.М., Жарков А.П., Култыгин О.П. Решение обратной задачи кинематики для последовательных роботов манипуляторов на основе нечетких численных методов // Прикладная информатика. 2022. Т. 17. № 4. С. 113–126. doi: 10.37791/2687-0649-2022-17-4-113-126. References 1. Filaretov, V.F., Klimchik, A.S., Yukhimets, D.A., Konoplin, A.Yu., Zuev, A.V. (2020) ‘Intelligent underwater robotics for inspection and process operations on offshore gas pipelines and production systems’, Gas Industry J., (8), pp. 30–38 (in Russ.). 2. Balabanov, A.N., Bezuglaya, A.E., Shushlyapin, E.A. (2021) ‘Underwater robot manipulator control’, Informatics and Automation, 20(6), pp. 1307–1332 (in Russ.). doi: 10.15622/ia.20.6.5. 3. Timofeev, A.N., Rakshin, E.A., Zarutskiy, N.V. (2022) ‘A robotic system for repair and monitoring of hard-to-reach equipment’, Science and Business: Ways of Development, (4), pp. 193–196 (in Russ.). 4. Meshchanov, A.S., Gubaeva, E.I. (2020) ‘Control of aircraft manipulators in sliding modes with drive inertia and non-invariance to perturbations’, Herald of Technological University, 23(7), pp. 100–108 (in Russ.). 5. Kositsyn, A.A., Bogomolov, A.S., Kushnikov, V.A. (2024) ‘The task of reducing the probability of developing combinations of emergency events in unmanned aerial vehicles’, J. of Applied Informatics, 19(4), pp. 18–34 (in Russ.). doi: 10.37791/2687-0649-2024-19-4-18-34. 6. Ignatyev, V.V. (2023) ‘Compensation of various types of uncertainties when controlling a technical object using intelligent controllers’, Software & Systems, 36(3), pp. 423–431 (in Russ.). doi: 10.15827/0236-235X.143.423-431. 7. Eremeev, A.P., Sergeev, M.D., Petrov, V.S. (2023) ‘Integration of reinforcement learning methods and fuzzy logic for intelligent real-time systems’, Software & Systems, 36(4), pp. 600–606 (in Russ.). doi: 10.15827/0236-235X.144.600-606. 8. Goharimanesh, M., Mehrkish, A., Janabi-Sharifi, F. (2020) ‘A fuzzy reinforcement learning approach for continuum robot control’, J. of Intelligent & Robotic Systems, 100, pp. 809–826. doi: 10.1007/s10846-020-01237-6. 9. Puchkov, A.Yu., Dli, M.I., Tindova, M.G. (2023) ‘A method for solving the inverse kinematics problem based on reinforcement learning for controlling robotic manipulators’, J. of Applied Informatics, 18(6), pp. 120–133 (in Russ.). 10. Borisov, V.V. (2020) ‘Fuzzy cognitive models for the research of complex systems and processes’, Speech Technology, (1-2), pp. 48–62 (in Russ.). doi: 10.58633/2305-8129_2020_1-2_48. 11. Chen, C.-T., Chiu, Y.-T. (2021) ‘A study of dynamic fuzzy cognitive map model with group consensus based on linguistic variables’, Technological Forecasting and Social Change, 171, art. 120948. doi: 10.1016/j.techfore.2021.120948. 12. Nair, A., Reckien, D., van Maarseveen, M.F.A.M. (2019) ‘A generalised fuzzy cognitive mapping approach for modelling complex systems’, Applied Soft Computing, 84, art. 105754. doi: 10.1016/j.asoc.2019.105754. 13. Borisov, V.V., Avramenko, D.Yu. (2021) ‘Fuzzy situational control of complex systems based on their composite hybrid modeling’, Systems of Control, Communication and Security, (3), pp. 207–237 (in Russ.). 14. Starodubtsev, M., Bilousov, M., Kamardin, S., Makarenko, H., Shybanov, S. (2024) ‘Models of technological processes management under conditions of uncertainty’, J. of Natural Sci. and Tech., 3(1), pp. 254–258. 15. Dobrynin, A.S., Gudkov, M.Yu., Koynov, R.S. (2020) ‘A precedent approach to incident management in automated process control systems’, Software Systems and Computational Methods, (2), pp. 45–52 (in Russ.). doi: 10.7256/2454-0714.2020.2.31040. 16. Chernovalova, M.V. (2021) ‘Fuzzy case models for project managementusing a multi-ontology approach’, J. of Applied Informatics, 16(2), pp. 4–16 (in Russ.). doi: 10.37791/2687-0649-2021-16-2-4-16. 17. Dli, M.I., Chernovalova, M.V., Sokolov, A.M., Morgunova, E.V. (2023) ‘Fuzzy dynamic ontological model for decision support of energy-intensive systems management based on precedents’, J. of Applied Informatics, 18(5), pp. 59–76 (in Russ.). doi: 10.37791/2687-0649-2023-18-5-59-76. 18. Melikhov, A.N., Bershteyn, L.S., Korovin, S.Ya. (1990) Situational Advising Systems with Fuzzy Logic. Мoscow, 272 p. (in Russ.). 19. Borisov, V.V., Sokolov, A.M., Zharkov, A.P., Kultygin, O.P. (2022) ‘Solving the inverse kinematics problem for sequential robot manipulators based on fuzzy numerical methods’, J. of Applied Informatics, 17(4), pp. 113–126 (in Russ.). doi: 10.37791/2687-0649-2022-17-4-113-126. |
http://swsys.ru/index.php?id=5120&lang=%5C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Компонентный подход: модуль правдоподобного вывода по прецедентам
- Информационная система управления движением продукции на складах
- Система назначения персонифицированного лечения по аналогии на основе гибридного способа извлечения прецедентов
- Автоматизированная система поддержки принятия решений для прогнозирования процессов рассеивания химически опасных веществ
- Программная реализация модуля анализа данных на основе прецедентов для распределенных интеллектуальных систем

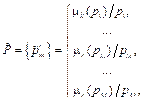
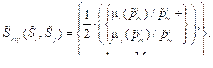 (3)
(3)






