Повышение достоверности приема информации при заданной скорости ее передачи в спутниковых системах связи
| Бобров А.И. () - , Бобров С.И. (sb@snt.ua) - Дочернее предприятие «ЭС ЭНД ТИ Украина», Киев, Украина | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Достоверность (верность) [3] приема дискретной информации, то есть вероятность правильного приема переданного символа, тем больше, чем меньше вероятность ошибочного его отождествления с любым другим символом из другого ансамбля. Поскольку вероятность ошибки рош и вероятность правильного приема рпр символа образуют полную группу событий, то рош + рпр =1. Отсюда следует, что достоверность D приема дискретной информации равна
Для подавляющего числа методов модуляции и типов применяемых сигналов [1, 8]
где А – коэффициент, определяемый методом модуляции (A<1):
х=х(q2) – функция, монотонно возрастающая с ростом q2, вид которой определяется типом применяемых сигналов, здесь
где Е – энергия элементарного сигнала, транспортирующего информационный символ; N – усредненная спектральная плотность мощности аддитивной гаусовской помехи в полосе частот, занимаемой спектром сигнала. Согласно (1) и (2):
Из (3) и (4) следует, что независимо от типов применяемых сигналов и методов модуляции достоверность приема дискретной информации растет, приближаясь к единице, с увеличением энергии сигнала. Поскольку энергия дискретного финитного сигнала определяется выражением:
где P(t) – мгновенная мощность сигнала; ТС – длительность сигнала; РСР= Из (5) следует, что при ограниченной пико- вой мощности РПИК сигнала и заданной его длительности ТС энергия Е достигает макси- мума в том случае, когда форма огибающей сигнала прямоугольная с длительностью ТС и P(t)=РПИК=const. Поскольку возможность увеличения энергии сигнала увеличением его пиковой мощности ограничена Регламентом радиосвязи [6], установившим верхний предел на эквивалентную изотропно-излучаемую мощность наземных и земных станций, а также пределом на плотность мощности в эталонной полосе частот у поверхности Земли, создаваемой космическими станциями, то энергию сигнала в настоящее время можно практически увеличивать только за счет увеличения длительности ТС. Однако с увеличением ТС уменьшается техническая скорость передачи сигналов RT=TC-1, а пропорционально ей – и скорость передачи информации RИ. Так, при передаче m-позиционных сигналов по симметричным каналам [4,5]
где RK – скорость кода ( Если элементарные m-позиционные сигналы простые, то есть произведение длительности ТС на ширину полосы частот ПС, занимаемой их спектром, порядка единицы, увеличение ТС влечет за собой соответствующее уменьшение ПС. В этом случае попытка сохранить прежнее значение RИ при увеличении ТС путем сохранения прежней частоты следования элементарных сигналов ведет к появлению (нарастанию) межсимвольных искажений, что влечет за собой уменьшение достоверности передачи информации и увеличение результирующей пиковой мощности интерферирующих между собой наложившихся во времени друг на друга соседних элементарных сигналов, а это повлечет за собой необходимое, согласно требованиям Регламента радиосвязи [6], уменьшение пиковой мощности каждого элементарного сигнала примерно в Однако проблема просто решаема на основе сложных элементарных сигналов с большой базой, у которых ТС×ПС=ВС>>1 и ширина полосы частот, занимаемой их спектром ПС, такая же, как у первоначального простого сигнала П0, то есть база сигнала увеличена не за счет увеличения ширины его спектра, а за счет увеличения его длительности. Кроме того, эти сложные сигналы при наложении во времени друг на друга не должны интерферировать друг с другом, чтобы каждый мог иметь максимально возможную пиковую мощность, ограниченную лишь требованиями Регламента радиосвязи. Такими сложными сигналами, в частности, являются широкоизвестные радиоимпульсы с прямоугольной огибающей амплитуд и линей- но-частотно-модулированным (ЛЧМ) запол- нением. Большие значения базы ЛЧМ импуль- сов достаточно точно описываются выражением [3] ВС = 2FДТС, где 2FД – полная девиация час- тоты. Кроме этого, при ВС>>1 огибающая амплитудного спектра ЛЧМ импульсов с прямоугольной огибающей амплитуд также близка к прямоугольной [3], то есть, если ЛЧМ-импульс во времени описывается выражением
то его спектральная плотность выражается как
В (6) и (7) f0 – средняя частота ЛЧМ заполнения импульса; t – текущее время. Корреляционная функция сигнала (6) имеет вид:
где
Поскольку сигнал на выходе согласованного фильтра с точностью до постоянного коэффициента r совпадает с автокорреляционной функцией его входного сигнала [3], то сигнал (6) после оптимальной фильтрации имеет вид: АВЫХ(z)=VВЫХ(z)×cos2pf0z , (8) где Длительность главного лепестка выходного сигнала (8) по ближайшим к максимуму нулям:
Так как нули огибающей сигнала (8) отстоят от главного лепестка на интервалы, кратные 0,5 ТВЫХ, то для исключения взаимных помех все сигналы должны следовать с периодом ТП=0,5ТВЫХ. Поскольку принято, что 2FД=П0, то ТВЫХ= В этом случае энергия сложного сигнала ЕС:
где В качестве примера рассмотрим случай относительной фазовой манипуляции, при которой в (2): А=1, Пусть при использовании простого элементарного сигнала обеспечивается достоверность приема информации, равная 0,999, которая соответствует (согласно таблице значений инте грала вероятностей [2]) х=3,295. Если увеличить базу сигнала всего лишь в 4 раза, то достовер ность приема информации возрастет до величины 0,9999999999, то есть вероятность ошибки при приеме дискретного элемента сигнала уменьшится с 10-3 до 10-10, то есть на 7 поряд- ков. Этот пример иллюстрирует значительную эффективность рассмотренного способа увеличения достоверности приема информации, который в определенных условиях позволяет получить еще и большую скорость передачи информации за счет отказа от ставшего ненужным помехоустойчивого кодирования. Список литературы 1. Абдулаев Д.А., Арипов М.Н. Передача дискретных сообщений в задачах и упражнениях. – М.: Радио и связь, 1985. – 128 с. 2. Большаков В.Д. Теория ошибок наблюдений с основами теории вероятностей. – М.: Недра, 1965. - 184 с. 3. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Радио и связь, 1986. - 512 с. 4. Зюко А.Г. Помехоустойчивость и эффективность систем связи. – М.: Связь, 1972. - 360 с. 5. Петрович Н.Т., Камнев Е.Ф., Каблукова М.В. Космическая связь. – М.: Сов. радио, 1979. - 280 с. 6. Регламент радиосвязи. - Женева, 1998. - Т.1. 7. Теория электрической связи. /Под ред. проф. Д.Д. Кловского. – М.: Радио и связь, 1998. - 432 с. 8. Устройства преобразования сигналов передачи данных./ Данилов Б.С., Стукалов С.В., Тамм Ю.А., Штейнбок М.Г. – М.: Связь, 1979. - 128 с. 9. Харкевич А.А. Борьба с помехами.-М.: ГИФМЛ, 1963. - 276 с. 10. Цымбал В.П. Теория информации и кодирования. – К.: Вища шк., 1992. - 263 с. |
http://swsys.ru/index.php?id=516&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Автоматизированная информационная система маркетолога
- Система автоматизации процессов рабочего проектирования сложного изделия
- Информационная система оптимизации расписания доставки грузов от производителей сырья
- Интегрированная система «микросреда»
- Нейроподобная сеть для решения задачи оптимизации антенной решетки

 . (1)
. (1) , (2)
, (2) – функция Крампа (интеграл вероятностей), где
– функция Крампа (интеграл вероятностей), где , (3)
, (3) . (4)
. (4) , (5)
, (5) – средняя мощность сигнала, то увеличить ее можно: а) увеличением РСР при фиксированном значении ТС; б) увеличением ТС при фиксированном значении РСР; в) одновременным увеличением РСР и ТС.
– средняя мощность сигнала, то увеличить ее можно: а) увеличением РСР при фиксированном значении ТС; б) увеличением ТС при фиксированном значении РСР; в) одновременным увеличением РСР и ТС.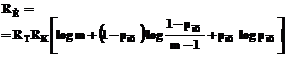 ,
, ) [7].
) [7]. [10] раз, где n – количество наложившихся друг на друга элементарных сигналов. Таким образом, при неизменных типах модуляции и кодирования невозможно на основе простых сигналов увеличением их длительности сохранить скорость передачи дискретной информации и увеличить ее достоверность.
[10] раз, где n – количество наложившихся друг на друга элементарных сигналов. Таким образом, при неизменных типах модуляции и кодирования невозможно на основе простых сигналов увеличением их длительности сохранить скорость передачи дискретной информации и увеличить ее достоверность. , (6)
, (6) . (7)
. (7) ,
, – энергия сигнала (6);
– энергия сигнала (6); .
. – огибающая радиосигнала, в котором z=(t-TC) – время, отсчитываемое от ТС.
– огибающая радиосигнала, в котором z=(t-TC) – время, отсчитываемое от ТС. .
. =2Т0 и ТП=
=2Т0 и ТП= , где Т0 – длительность исходного простого элементарного сигнала и база сложного ЛЧМ-сигнала ВС=П0ТС=П0Т0kT=kT, где
, где Т0 – длительность исходного простого элементарного сигнала и база сложного ЛЧМ-сигнала ВС=П0ТС=П0Т0kT=kT, где  – коэффициент увеличения длительности простого сигнала при переходе к сложному.
– коэффициент увеличения длительности простого сигнала при переходе к сложному.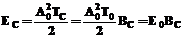 ,
, – энергия простого исходного сигнала.
– энергия простого исходного сигнала. .
.