Реализация временных рассуждений для интеллектуальных систем поддержки принятия решений реального времени
| Еремеев А.П. (eremeev@appmat.ru) - Национальный исследовательский университет «Московский энергетический институт» (профессор), г. Москва, Россия, доктор технических наук, Куриленко И.Е. (ivan@appmat.ru) - Национальный исследовательский университет «Московский энергетический институт», г. Москва, Россия, кандидат технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Для создания перспективных интеллектуальных систем поддержки принятия решений реального времени (ИСППР РВ) (рис. 1), предназначенных для мониторинга и управления сложными техническими объектами и процессами, необходимо реализовать быстрый и надежный механизм моделирования временных рассуждений [1-3].
Основные элементы системы временных рассуждений Информация о времени обычно представляется в виде временных зависимостей между временными примитивами. В качестве таких примитивов обычно используются моменты времени, интервалы или и то, и другое. Зависимости (отношения) между временными примитивами трактуются как ограничения на их реальное время появления (расположение во времени). Поэтому отношения между этими примитивами обычно представляются как качественные бинарные ограничения. Эти ограничения задаются на основе множества базовых временных (темпоральных) отношений (BTR) между временными примитивами, элементы которого должны быть взаимно исключающими, и их объединение должно являться универсальным ограничением, то есть ограничением, которое содержит все возможные отношения и, следовательно, не накладывает каких-либо ограничений. Так как основная цель временных рассуждений состоит в определении того, что следует из множества заданных временных ограничений (а это могут быть в основном новые ограничения, для непротиворечивых входных множеств), обработка временной информации обычно представляется как задача согласования временных ограничений (ЗСВО). Так как ИСППР РВ ориентирована на оперирование с неточной и неполной информацией, то возникает проблема представления неточных временных отношений. Для этого вводится дизъюнктивная форма временных ограничений: Формула В зависимости от выбора временных примитивов различаются точечная (на базе моментов времени), интервальная (на базе интервалов времени) и интервально-точечная (допустимы и моменты, и интервалы) модели времени. Различные модели отличаются как сложностью, так и выразительными способностями. Известно, что интервальная модель времени, в основе которой лежит интервальная алгебра Аллена [4] и понятие отношения меду парой интервалов, является более выразительной, чем точечная, но при этом характеризуется большой вычислительной сложностью. В конкретной модели времени за счет изменения набора базовых отношений также можно менять выразительность представляемой временной информации. В рамках точечной модели времени, например, можно рассматривать следующие три алгебры временных отношений: · базовую точечную алгебру (BPA) с набором отношений (Ø, · выпуклую точечную алгебру (CPA) с набором отношений (Ø, · точечную алгебру (PA) с набором отношений (Ø, где символами Ø и U обозначены соответственно пустое и универсальное отношения.
Решение ЗСВО Качество решения ЗСВО непосредственно зависит от способа представления временной информации, наиболее удачным из которых является использование графов. В системе Time Graph (ориентированной на работу с точечной алгеброй и реализованной в среде Common Lisp), которая в определенной степени взята в качестве прототипа предлагаемой СВР, для представления информации о времени применены графы, взвешенные временной информацией (TL-графы) [5]. TL-граф определяется как граф, содержащий, по крайней мере, одну вершину и набор взвешенных ребер. Каждое ребро (w,l,v) графа соединяет пару различных вершин w и v отношением l Однако из определения TL-графа следует, что равенство двух моментов времени может быть представлено только с помощью нестрогих отношений « Обозначим P – множество имен временных переменных, а V – множество вершин MTL-графа. Предположим, что существует сюрьективная функция Интерпретацией MTL-графа G называется тройка , где T – упорядоченное множество; I – функция Моделью MTL-графа G называется такая интерпретация, при которой справедливо следующее утверждение: если MTL-граф согласуем (непротиворечив), если он имеет, по крайней мере, одну модель. Два или более MTL-графа логически эквивалентны, если они обладают одними и теми же моделями. Из приведенных выше определений непосредственно следует, что MTL-граф согласуем тогда и только тогда, когда он не содержит ни одного <- или £-цикла, который содержит две вершины, соединенные ребром, взвешенным отношением Множество S отношений, заданных в терминах точечной модели времени, достаточно просто преобразовать в MTL-граф. На первом этапе этого преобразования каждой переменной из S сопоставляется одна вершина графа. Отношение эквивалентности x=y преобразуется в неориентированную связь Алгоритм определения согласованности MTL-графа G=(V,E), где V и E – множества вершин и ребер соответственно состоит из следующих шагов: 1) определение всех компонент сильной связности в G без учета связей, взвешенных отношением 2) поиск среди всех компонент сильной связности компонента, содержащего пару вершин, между которыми существует связь, взвешенная отношением < или Получаемый в результате граф является ациклическим и логически эквивалентен исходному MTL-графу. Таким образом, MTL-граф G может быть проверен на согласованность и свернут в случае его согласованности в логически эквивалентный ациклический MTL-граф за полиномиальное время O(e), где e – число связей в исходном MTL-графе G. Рассмотрим механизм выявления всех выполнимых отношений в сети ограничений, заданной MTL-графом. Предварительно введем понятие неявного отношения. MTL-граф содержит неявное отношение < между вершинами Явным MTL-графом для MTL-графа G называется ациклический MTL-граф, логически эквивалентный исходному графу G и не содержащий неявных отношений. Из определения явного MTL-графа следует, что: · v=w тогда и только тогда, когда v и w альтернативные имена одной и той же вершины (или v и w были связаны отношением =). · v · v≤w тогда и только тогда, когда существует ≤-путь от v к w. · v≠w тогда и только тогда, когда существует <-путь от v к w или в графе существует связь между v и w, взвешенная отношением ≠. Временной граф (Time-граф) – это явный MTL-граф, распадающийся на набор временных цепей (под временной цепью понимается ≤-путь), причем каждая вершина может принадлежать одной и только одной временной цепи. Очевидно, что различные цепи Time-графа могут быть соединены перекрестными связями. Таким образом, если произвести переход от MTL-графа к Time-графу, то будут автоматически решены следующие подзадачи, возникающие при решении ЗСВО: 1) определение согласованности множества ограничений (задача выполнимости). Действительно, MTL-граф согласуем, если он не содержит ни одного <-цикла и ни одного ≤-цикла, который содержит две вершины, соединенные ребром, взвешенным отношением ≠, а Time-граф – это ациклический по определению граф; 2) выявление всех выполнимых ограничений. Следует из того, что Time-граф – это явный MTL-граф. Преобразование MTL-графа в Time-граф включает четыре этапа. На первом этапе проверяется согласованность исходного множества временных ограничений. Так как СВР ориентирована на динамическое изменение этого множества (динамическое добавление новых переменных и отношений между ними в исходный набор бинарных ограничений), то на этом этапе не производится модификации MTL-графа, а по исходному MTL-графу строится новый граф, который на последующих этапах достраивается до Time-графа. Это позволяет сократить время перехода. Последующие этапы выполняются только для согласованных ЗСВО. На втором этапе осуществляется расстановка рангов; на третьем – распределение вершин графа по временным цепям. Заключительным этапом является выявление всех неявных отношений < в графе. При успешном завершении преобразования СВР способна выполнять определение точного отношения между заданной парой временных переменных. Для этого определяются соответствующие им вершины Time-графа. Затем в общем случае производится поиск всех путей между этими вершинами, причем использованная структура данных (ранги и временные цепи) позволяет сократить время поиска. Таким образом, ЗСВО для качественной точечной модели времени может быть сведена к задаче преобразования ЗСВО в МTL-граф и задаче преобразования МTL-графа в Time-граф. Представление неточной информации Представление неточных временных отношений в точечной алгебре (PA-дизъюнкции) и оперирование ими позволяет значительно повысить выразительность модели времени. Для этого используются отношения уже упоминавшейся ранее интервальной алгебры Аллена. Временным интервалом X называется упорядоченная пара ( В таблице 1 представлены 13 базовых отношений интервальной алгебры Алена [4]. К сожалению, в общем случае ЗСВО для данной алгебры является NP-полной. Для сокращения времени поиска решения возможны следующие подходы [2]. Первый подход основан на ограничении класса интервальных временных отношений его подмножеством (SIA-подмножеством) отношений, которые могут быть представлены в виде конъюнкций отношений в точечной алгебре между точками начала и конца интервала. Другой подход связан с использованием интервальной алгебры в полном ее объеме, но с применением полиномиального алгоритма поиска решения, который, однако, гарантирует решение ЗСВО только в случае согласованности исходного множества интервальных отношений (то есть несогласованность может быть не обнаружена, что приведет к безрезультатному завершению алгоритма). Отметим, что главным недостатком первого подхода является невозможность представления дизъюнктивных отношений между интервалами времени, что часто необходимо для решения практических задач. Использование второго подхода вообще практически нецелесообразно, так как получаемый при этом планировщик может давать несогласованные (то есть невыполнимые) планы. Как уже отмечалось, целью обработки дизъюнктивных отношений является повышение выразительности модели времени в случае неточной исходной информации, а следовательно, и расширение границ практического применения СВР. Наиболее просто в точечной алгебре представим класс отношений на основе SIA-подмножества. Каждый интервал X можно представлять в виде точек его начала ( Другим способом является добавление в модель времени средств поддержки и обработки бинарных PA-дизъюнкций, что позволяет оперировать со значительно большим, чем SIA, подклассом интервальной алгебры (можно представить, по крайней мере, Соответствия между отношениями точечной алгебры и отрицаниями базовых отношений интервальной алгебры представлены в таблице 2. Таблица 2 Таблица преобразований отрицаний базовых отношений интервальной алгебры в отношения в точечной алгебре
Из таблицы видно, что только отрицание двух (overlaps, overlapped-by) из тринадцати базовых отношений приводит к появлению тернарных PA-дизъюнкций. Таким образом, число интервальных отношений, которые могут быть представлены с помощью бинарных PA-дизъюнкций, составляет Рассмотрим возможность оперирования неточной (нечеткой) информацией. Дизъюнктивным Time-графом называется пара , где T – Time-граф; D – набор бинарных дизъюнкций в точечной алгебре. Элементами множества D являются Дизъюнктивный Time-граф называется явным, если он согласован и не содержит неявных отношений. Следовательно, для получения явного дизъюнктивного Time-графа необходимо определить реализацию множества бинарных дизъюнкций D для графа T. В общем случае для решения этой задачи для k дизъюнкций в множестве D необходимо проверить Определение согласованности дизъюнктивного Time-графа в общем случае является NP-полной задачей. Для сокращения времени поиска решения можно использовать следующий алгоритм. На первом (предварительном) шаге выполняется попытка сокращения множества (поискового пространства) D до его подмножества D' и построение Time-графа T' таким образом, что реализация D' для графа T' является подмножеством реализации D для графа T. Назовем этот этап этапом предварительной обработки дизъюнкций. На втором шаге производится поиск реализации D' для графа T' с использованием алгоритма поиска с возвратами. Рассмотрим правила построения подмножества D', которые применяются к каждой дизъюнкции Di в исходном множестве D. Для иллюстрации будем использовать пример на рисунке 3. Из графа T следует, что a Сформулируем правила сокращения поискового пространства, предварительно введя множество Q, состоящее из PA-отношений, которые должны быть в каждой реализации множества бинарных дизъюнкций D для графа T: 1. T-выводимость (T-derivability). Если в графе T имеется связь (отношение) 2. T-тавтология (T-tautology): a) если добавление в граф T связи b) если добавление в граф T связи 3. T-резолюция (T-resolution): a) если добавление в граф T связи б) если добавление в граф T связи
Если дизъюнкция Di не удовлетворяет ни одному из правил 1-3, то она должна быть включена в множество D'. На заключительном этапе предварительной обработки дизъюнкций к графу T должно быть применено множество Q, и в результате будет получен граф T'. Если граф T' несогласован, то исходный дизъюнктивный Тime-граф также несогласован. Таким образом, дизъюнкции D2 и D4 (рис. 3) не включаются в множество D', так как выполняются соответственно правила 1 и 2, а дизъюнкции D1 и D3 не включаются в D', так как выполняется правило 3. Полученный в итоге сокращения поискового пространства дизъюнктивный Time-граф приведен на рисунке 4.
4. Модифицированная T-тавтология: если для графа T справедливо ( Правило 4 должно проверяться только для дизъюнкций вида Примечательно, что второй этап обработки дизъюнкций, требующий значительных затрат времени, не нужен для определенных исходных наборов дизъюнкций, например, в случае использования ORD-Horn подкласса интервальной алгебры [5]. Этот подкласс является уникальным подклассом, содержащим все тринадцать базовых временных отношений, для которого существует полиномиальная стратегия применения правил сокращения пространства поиска при определении согласованности дизъюнктивного Time-графа , где D – множество бинарных ORD-высказываний (то есть высказываний вида xRy, где R
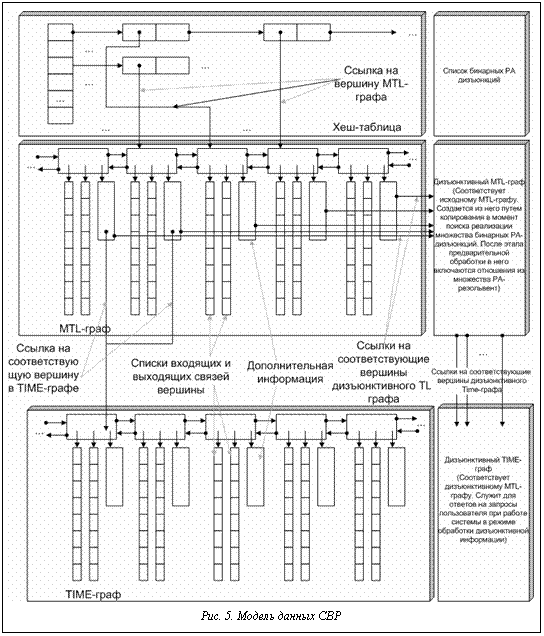
СРВ. Рассмотрим архитектуру и основные возможности СВР, предназначенные для использования в составе ИСППР РВ. СВР реализована в виде набора отдельных модулей, объединенных модулем контроля. Общение с системой осуществляется через фиксированный интерфейс связи, что позволяет легко встраивать ее в клиентские приложения. СВР позволяет пользователю управлять: · контролем согласованности: поддерживаются режимы автоматического контроля целостности внутренних данных и контроля согласованности по запросу систем-клиентов; · выразительностью используемой модели времени: поддерживается выбор среди моделей BPA, CPA, PA, SIA, ORD-Horn, PA-дизъюнкции; · шагами выполнения преобразования MTL-графа в Time-граф. Интерфейс связи СВР в полной мере обеспечивает набор необходимых системе-клиенту возможностей для оперирования временными зависимостями: - создание временных переменных; - создание отношения между двумя временными переменными; - удаление временных переменных; - удаление отношений между временными переменными из базы; - проверку на существование временной переменной в базе и выдачу информации о переменной, если она существует; - управление системой контроля (непрерывный/по запросу) согласованности; - нахождение согласующего сценария; - определение выполнимых ограничений между заданной парой временных примитивов; - - выявление всех выполнимых ограничений. В режиме автоматического контроля СВР поддерживает транзакции и автоматический откат к последнему согласованному состоянию в случае появления ошибки согласованности. Для реализации временных рассуждений необходимы средства представления множества временных переменных, сети ограничений в виде MTL-графа, множества бинарных PA-дизъюнкций. Исходя из это- го для СВР была предложена модель данных, представленная на рисунке 5. Рассмотрим схему функционирования СВР (рис. 6). На этапе преобразования множества ограничений в MTL-граф производится заполнение хэш-таблицы именами временных переменных. В этой таблице в качестве дополнительной информации для каждого имени переменной хранится ссылка на вершину TL-графа, что позволяет быстро производить поиск вершин TL-графа по имени. Наиболее эффективным способом хранения ориентированного графа ограничений в СВР является его представление в виде списка вершин. Каждая вершина описывается списками входящих в нее и выходящих связей. Реализация графа на основе двунаправленных списков позволяет динамическое изменение текущего набора ограничений в точечной алгебре и, следовательно, соответствующего TL-графа. В качестве дополнительной информации, для каждой вершины MTL-графа хранятся ссылка на соответствующую вершину в Time-графе, код компонента связности и т.д. Структура Time-графа аналогична структуре MTL-графа. Отличие составляет лишь набор хранимой для каждой вершины дополнительной информации: ранг, код цепи, метасвязи и т.д. Запросы на поиск выполнимых отношений между любыми двумя временными примитивами выполнятся на Time-графе. СВР автоматически обеспечивает преобразование символьных имен переменных, которыми оперирует система-клиент в соответствующую ей вершину Time-графа. При этом производится поиск вершины MTL-графа, соответствующей имени переменной в хеш-таблице, а затем осуществляется поиск соответствующей этой вершине вершины Time-графа. При обработке бинарных PA-дизъюнкций предусмотрена возможность представления набора дизъюнкций, дизъюнктивного TL-графа и дизъюнктивного Time-графа. Эти структуры не используются, если система работает с точной информацией (когда запрещено внесение дизъюнктивных ограничений). Если же обрабатывается нечеткая информация, то при каждом запросе на поиск реализации множества дизъюнкций в дизъюнктивной модели TL-граф и Time-граф обновляются. Запросы на поиск выполнимого отношения между любыми двумя временными переменными ведутся в дизъюнктивном Time-графе. Внесение в модель данных дополнительного дизъюнктивного TL-графа сделано из соображений повышения эффективности обработки.
Данная СВР включена в состав прототипа ИСППР РВ для оперативно-диспетчерского персонала энергоблока. Список литературы 1. Вагин В.Н., Еремеев А.П. Некоторые базовые принципы построения интеллектуальных систем поддержки принятия решений реального времени // Изв. РАН. Теория и системы управления. - 2001. - № 6. - С.114-123. 2. Еремеев А.П., Троицкий В.В. Модели представления временных зависимостей в интеллектуальных системах поддержки принятия решений // Там же. - 2003. - № 5. - С.75-88. 3. Кандрашина Е.Ю., Литвинцева Л.В., Поспелов Д.А. Представление знаний о времени и пространстве в интеллектуальных системах. / Под ред. Д.А. Поспелова. - М.: Наука. - Гл. ред. физматлит., 1989. 4. Allen J.F., Ferguson G. Actions and Events in Interval Temporal Logic. // Technical Report, S21, 1994. 5. Gereviny A. and Schubert L. Efficient Algorithms for Qualitative Reasoning about Time. Technical report 496, Department of Computer Science, University of Rochester, Rochester, NY, 1993 6. Еремеев А.П. Об интеграции моделей в интеллектуальных системах поддержки принятия решений // Девятая национальная конф. по искусствен. интеллекту с междунар. участ. КИИ-2004 (28 сент.- 2 окт. 2004 г., Тверь): Тр. конф. В 3 т. Т.2. М.: Физматлит, 2004.- С.815-823. 7. Еремеев А.П., Денисенко Л.А. Прототип интеллектуальной системы поддержки принятия решений для управления энергообъектом // Программные продукты и системы. - 2002. - №3.- С.38-41. |
http://swsys.ru/index.php?id=526&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
- Метод оценки безопасности информации в автоматизированных системах
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Эвристические и точные методы программной конвейеризации циклов

 По сути, во всех основных блоках ИСППР РВ, включая базы данных и знаний, необходимо иметь средства представления фактора времени и временных (темпоральных) зависимостей, на основе которых моделируются и временные рассужде- ния [2]. Системный подход к построению сложных программных комплексов, к которым относятся ИСППР РВ, требует реализации системы временных рассуждений как самостоятельной подсистемы (модели в базе моделей) в составе ИСППР РВ. Это позволяет избежать дублирования программного кода за счет его повторного использования в других компонентах (блоках и моделях). Таким образом, базовый инструментарий для разработчика ИСППР РВ должен включать готовую реализацию такой подсистемы, которая содержит средства представления и алгоритмы обработки временной информации. В данной работе рассматривается реализация системы временных (темпоральных) рассуждений (СВР) на основе точечной модели времени, достоинствами которой в плане использования в ИСППР РВ является относительная простота реализации и наличие алгоритмов вывода с полиномиальной оценкой сложности.
По сути, во всех основных блоках ИСППР РВ, включая базы данных и знаний, необходимо иметь средства представления фактора времени и временных (темпоральных) зависимостей, на основе которых моделируются и временные рассужде- ния [2]. Системный подход к построению сложных программных комплексов, к которым относятся ИСППР РВ, требует реализации системы временных рассуждений как самостоятельной подсистемы (модели в базе моделей) в составе ИСППР РВ. Это позволяет избежать дублирования программного кода за счет его повторного использования в других компонентах (блоках и моделях). Таким образом, базовый инструментарий для разработчика ИСППР РВ должен включать готовую реализацию такой подсистемы, которая содержит средства представления и алгоритмы обработки временной информации. В данной работе рассматривается реализация системы временных (темпоральных) рассуждений (СВР) на основе точечной модели времени, достоинствами которой в плане использования в ИСППР РВ является относительная простота реализации и наличие алгоритмов вывода с полиномиальной оценкой сложности. , где k>0 и
, где k>0 и 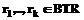 .
. {
{ }
} интерпретируется как
интерпретируется как  . То есть между временными переменными
. То есть между временными переменными  для каждого дизъюнктивного ограничения, что они не противоречат друг другу.
для каждого дизъюнктивного ограничения, что они не противоречат друг другу. ),
), ),
), ),
), Более эффективной в плане реализации является BPA, а наиболее выразительной – PA. В рамках интервальной модели времени также можно вести ограничения на набор разрешенных отношений. Например, можно ограничить класс интервальных отношений подмножеством всех отношений в интервальной алгебре, которые могут быть представлены в виде конъюнкций отношений в точечной алгебре между точками начала и конца интервала [2]. Такой подкласс легко представим в рамках точечной алгебры, и для него существует полиномиальный алгоритм поиска решения. Более широкие подклассы интервальной алгебры также могут быть представлены в терминах точечной модели времени с использованием неточных отношений между моментами време- ни [2]. Целесообразно реализовать СВР так, чтобы можно было задать нужный уровень выразительности как для конкретной модели времени, так и для их совокупности.
Более эффективной в плане реализации является BPA, а наиболее выразительной – PA. В рамках интервальной модели времени также можно вести ограничения на набор разрешенных отношений. Например, можно ограничить класс интервальных отношений подмножеством всех отношений в интервальной алгебре, которые могут быть представлены в виде конъюнкций отношений в точечной алгебре между точками начала и конца интервала [2]. Такой подкласс легко представим в рамках точечной алгебры, и для него существует полиномиальный алгоритм поиска решения. Более широкие подклассы интервальной алгебры также могут быть представлены в терминах точечной модели времени с использованием неточных отношений между моментами време- ни [2]. Целесообразно реализовать СВР так, чтобы можно было задать нужный уровень выразительности как для конкретной модели времени, так и для их совокупности. {
{ }. Ориентированные ребра взвешиваются отношениями «меньше» (<) или «меньше или равно» (£), неориентированные – отношением «не равно» (¹). В системе предлагался ряд эффективных алгоритмов, базирующихся на сведении решения ЗСВО к последовательности операций над графами.
}. Ориентированные ребра взвешиваются отношениями «меньше» (<) или «меньше или равно» (£), неориентированные – отношением «не равно» (¹). В системе предлагался ряд эффективных алгоритмов, базирующихся на сведении решения ЗСВО к последовательности операций над графами. », что приводит к невозможности использования TL-графов для представления временной информации, заданной в терминах базовой точечной алгебры. Для устранения данного недостатка в системе Time Graph предложено использовать модифицированные TL-графы (MTL-графы). MTL-граф – это граф, содержащий, по крайней мере, одну вершину и набор взвешенных ребер. Каждое ребро (w,l,v) MTL-графа соединяет пару различных вершин w и v отношением l
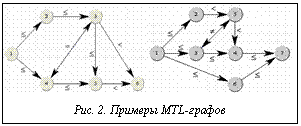
», что приводит к невозможности использования TL-графов для представления временной информации, заданной в терминах базовой точечной алгебры. Для устранения данного недостатка в системе Time Graph предложено использовать модифицированные TL-графы (MTL-графы). MTL-граф – это граф, содержащий, по крайней мере, одну вершину и набор взвешенных ребер. Каждое ребро (w,l,v) MTL-графа соединяет пару различных вершин w и v отношением l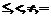 }. Ориентированные ребра, как и ранее, взвешиваются отношениями «меньше» (<) или «меньше или равно» (≤), а неориентированные – отношениями «не равно» (≠) и «равно» (=). Каждой вершине в графе соответствует, по крайней мере, один момент времени – временная переменная. Если какой-либо из вершин графа соответствует более одной переменной, то все они являются альтернативными именами одной и той же временной точки. Ситуация, когда одна и та же переменная соответствует более чем одной вершине, недопустима. На рисунке 2 приведены примеры MTL-графов.
}. Ориентированные ребра, как и ранее, взвешиваются отношениями «меньше» (<) или «меньше или равно» (≤), а неориентированные – отношениями «не равно» (≠) и «равно» (=). Каждой вершине в графе соответствует, по крайней мере, один момент времени – временная переменная. Если какой-либо из вершин графа соответствует более одной переменной, то все они являются альтернативными именами одной и той же временной точки. Ситуация, когда одна и та же переменная соответствует более чем одной вершине, недопустима. На рисунке 2 приведены примеры MTL-графов. , которая сопоставляет вершинам из множества V имена из множества P. Приведем понятия модели и интерпретации MTL-графа.
, которая сопоставляет вершинам из множества V имена из множества P. Приведем понятия модели и интерпретации MTL-графа. , такая, что для всех
, такая, что для всех  ,
, 
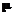 (
( – ребро в графе G, то для всех
– ребро в графе G, то для всех  и
и  , выполняется ),I(
, выполняется ),I( , а также не содержит ни одной группы вершин, объединенных отношениями =, < или
, а также не содержит ни одной группы вершин, объединенных отношениями =, < или  =
= , отношение неравенства x
, отношение неравенства x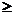 y преобразуется в направленные связи
y преобразуется в направленные связи  и
и  , если не существует ни одного <-пути от
, если не существует ни одного <-пути от  , от
, от  ,
, ) значений, причем
) значений, причем  – граничные точки интервала.
– граничные точки интервала. =2048 отношений из общего числа
=2048 отношений из общего числа  =8192 отношений в полной интервальной алгебре Аллена; в SIA-подмножестве представимо 188 отношений) [4,5].
=8192 отношений в полной интервальной алгебре Аллена; в SIA-подмножестве представимо 188 отношений) [4,5]. , где x,y,z,w – временные переменные;
, где x,y,z,w – временные переменные;  – отношения (
– отношения ( ); i=1,…,n. Определение согласованного TL-графа можно обобщить на случай дизъюнктивного Time-графа. Пусть в множество отношений точечной алгебры M входит по одному дизъюнкту из каждой бинарной дизъюнкции множества D. Дизъюнктивный Time-граф считается согласованным, если существует такое множество M, что добавление его в граф T не нарушает его согласованности. Множество M при этом называется реализацией множества бинарных дизъюнкций D для графа T.
); i=1,…,n. Определение согласованного TL-графа можно обобщить на случай дизъюнктивного Time-графа. Пусть в множество отношений точечной алгебры M входит по одному дизъюнкту из каждой бинарной дизъюнкции множества D. Дизъюнктивный Time-граф считается согласованным, если существует такое множество M, что добавление его в граф T не нарушает его согласованности. Множество M при этом называется реализацией множества бинарных дизъюнкций D для графа T. возможных вариантов реализаций, что ведет к экспоненциальной оценке сложности соответствующего алгоритма.
возможных вариантов реализаций, что ведет к экспоненциальной оценке сложности соответствующего алгоритма. или
или 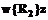 , то дизъюнкцию
, то дизъюнкцию 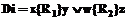 можно не включать в множество D'.
можно не включать в множество D'. приводит к появлению связи
приводит к появлению связи  , то дизъюнкцию
, то дизъюнкцию  приводит к появлению связи
приводит к появлению связи 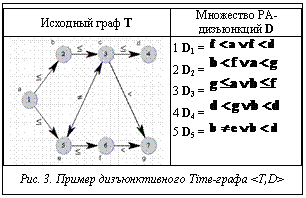 в) если добавление в граф T связи
в) если добавление в граф T связи 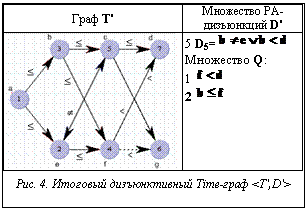 Следует заметить, что если не формировать множество Q, а добавлять его элементы в граф по мере их выявления, то в приведенном примере из множества поиска может быть исключена и PA-дизъюнкция D5. Но добавление в граф T новой связи требует полного его обновления (то есть всех изложенных выше шагов), что при частых добавлениях потребует значительного времени. Также полное обновление исходного графа требуется и при применении правила 2. Для сокращения вычислений в [5] предложено использовать упрощенное правило тавтологии (правило 4).
Следует заметить, что если не формировать множество Q, а добавлять его элементы в граф по мере их выявления, то в приведенном примере из множества поиска может быть исключена и PA-дизъюнкция D5. Но добавление в граф T новой связи требует полного его обновления (то есть всех изложенных выше шагов), что при частых добавлениях потребует значительного времени. Также полное обновление исходного графа требуется и при применении правила 2. Для сокращения вычислений в [5] предложено использовать упрощенное правило тавтологии (правило 4). ) или (
) или ( ), то дизъюнкцию
), то дизъюнкцию 
 можно не включать в множество D'.
можно не включать в множество D'. в случае, если эта дизъюнкция не удовлетворяет правилу 1.
в случае, если эта дизъюнкция не удовлетворяет правилу 1. }).
}). Если дизъюнктивный Time-граф построен не для множества отношений из ORD-Horn подкласса интервальной алгебры, то необходимо выполнить поиск реализации множества дизъюнкций D для графа T с использованием алгоритма поиска с возвратами или переборного алгоритма. Переборный алгоритм практически неприемлем, так как требует рассмотрения огромного числа возможных вариантов реализаций (в общем случае для k дизъюнкций в множестве D необходимо проверить
Если дизъюнктивный Time-граф построен не для множества отношений из ORD-Horn подкласса интервальной алгебры, то необходимо выполнить поиск реализации множества дизъюнкций D для графа T с использованием алгоритма поиска с возвратами или переборного алгоритма. Переборный алгоритм практически неприемлем, так как требует рассмотрения огромного числа возможных вариантов реализаций (в общем случае для k дизъюнкций в множестве D необходимо проверить 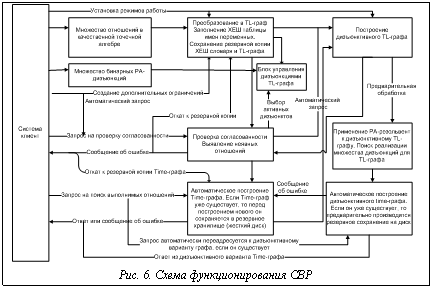 возможность автоматического отката к последнему согласованному состоянию;
возможность автоматического отката к последнему согласованному состоянию;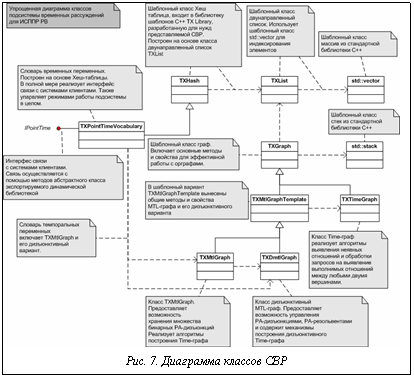 СВР реализована на языке C++ Builder 6.0 в виде DLL (Dynamic link library). Для повышения быстродействия системы создана библиотека шаблонов для языка C++, которая включает улучшенную реализацию таких важных для СВР примитивов, как список, стек, массив и граф. На основе списка были созданы шаблонные классы «граф» и «хеш-таблица». На основе шаблонного класса «граф» были созданы основные контейнеры модели данных – TL-граф, TIME-граф и их дизъюнктивные варианты. Таким образом, структура модели данных органично отражена в объектах системы. Основным управляющим классом, реализующим интерфейс связи и через него доступ к приложениям-клиентам, является словарь временных переменных (vocabulary). Диаграмма классов СВР как компонента ИСППР РВ приведена на рисунке 7.
СВР реализована на языке C++ Builder 6.0 в виде DLL (Dynamic link library). Для повышения быстродействия системы создана библиотека шаблонов для языка C++, которая включает улучшенную реализацию таких важных для СВР примитивов, как список, стек, массив и граф. На основе списка были созданы шаблонные классы «граф» и «хеш-таблица». На основе шаблонного класса «граф» были созданы основные контейнеры модели данных – TL-граф, TIME-граф и их дизъюнктивные варианты. Таким образом, структура модели данных органично отражена в объектах системы. Основным управляющим классом, реализующим интерфейс связи и через него доступ к приложениям-клиентам, является словарь временных переменных (vocabulary). Диаграмма классов СВР как компонента ИСППР РВ приведена на рисунке 7.