Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Развитие модели формирования бинокулярного изображения виртуальной 3D-среды
Аннотация:
Abstract:
| Автор: Афанасьев В.О. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 13328 |
Версия для печати Выпуск в формате PDF (1.31Мб) |
В большинстве существующих систем виртуальной реальности формирование начальных условий при построении бинокулярного изображения (стереопары) основано на модели так называемой стереоголовы, системы с 6-ю степенями свободы (6-DOF Stereo-Head, [1-3,11,12,14]), в которую входят две виртуальные камеры. Основным недостатками концепции стереоголовы является чрезмерно упрощенная модель формирования бинокулярного изображения 3D-среды, которая, по сути дела, представляет собой элементарную модель стереоскопа, появившуюся еще в XIX веке. При таком подходе создаются условия для искаженого бинокулярного изображения виртуальной среды в ближней зоне (на расстоянии 3-5 метров от наблюдателя), и основной причиной возникновения таких условий является игнорирование вергентных движений глаз [4-6] .
В том, что такое влияние имеет место, можно убедиться, проанализировав геометрическую схему на рисунке 1. Поскольку оптический центр глаза и центр его вращения b не совпадают, центр проекции смещается при вращении глаза. Величина смещения зависит от угла вергенции, и при значительных углах смещение необходимо учитывать. На фрагменте (а) показано, что при рассматривании 3D-сцены разные предметные точки A и B в пространстве в зависимости от ориентации глазного яблока (C и C¢ – оптические центры) могут проецироваться в одну или две точки на сетчатке. В то же время при рассматривании статичной проекции этой сцены точки проекции, соответствующие разным предметным точкам пространства, проецируются на сетчатку в одну и ту же точку (фрагмент (б)). Нарушение связи между аккомодацией и вергенцией. Между вергенцией и аккомодацией существует рефлекторная связь (она позволяет сфокусироваться на точке пространства, соответствующей ориентации зрительных осей [4-6]). Условия, при которых возникает смещение виртуальной плоскости аккомодации (соответствующей углу вергенции) по глубине, показаны на рисунке 2. Несоответствие ожидаемого положения плоскости аккомодации и действительного положения плоскости носителя изображения (монитора, проекционного экрана и т.п.) может вызывать ощущение зрительного дискомфорта, а в некоторых случаях кратковременную или длительную диплопию. В существующих HMD-системах для нейтрализации описанного фактора используются зеркальные и/или линзовые системы (например LEEP-оптика [11,12]), которые отодвигают плоскость аккомодации на расстояние более 3-5 метров. В результате мышечное напряжение глаз ослабляется, но одновременно создаются условия для формирования ложного кинестетического образа наблюдаемой 3D-среды, что для систем совмещенного погружения неприемлемо (иногда опасно).
Анализ влияния вергентного смещение центра проекции на изображение 3D-среды Рассмотрим геометрическую модель с редуцированым глазом радиусом r, перед которым на его зрительной оси размещены две предметные точки, разнесенные по глубине. Будем считать, что ближайшая предметная точка P1 находится от центра проекции на расстоянии H, а вторая предметная точка P2 удалена от нее на расстояние DH (рис. 3). В исходном положении обе предметные точки проецируются на сетчатке в одну точку p0. При повороте глаза вокруг своего центра вращения на угол g происходит смещение оптического центра хрусталика (центра проекции). В результате этого смещения проекции предметных точек будут попадать на сетчатке уже не на одну, а на две разные точки p1 и p2. Необходимо определить, насколько сильно влияет вергентное смещение центра проекции на изменение положения проекций предметных точек (может быть, его можно игнорировать, если оно мало).
Характерными величинами для параметров H и DH являются значения, превышающие 1м, поэтому с учетом величины S=rsing£5мм (считаем r»11мм, g£30, что является типичным [4,8,9]) хорды, образующиеся при пересечении линий проекций предметных точек с контуром кругового сечения глаза, можно считать почти параллельными основной оси зрения и совпадающими, так как угол a между ними очень мал (около 1°), но в то же время с учетом разрешающей способности сетчатки этот угол даже в пределах от 1¢ до 1° следует считать значительным. Необходимо более точно оценить величину этого угла и его поведение при перемещении предметных точек P1 и P2 по глубине. С учетом параксиального приближения (для характерных размеров глаза, объектов и расстояний в наблюдаемой сцене) имеем следующие соотношения a » D/H, D/S » DH/(H+DH), откуда, учитывая, что S = r sing, имеем a» r sing DH / H(H+DH). В зависимости от положения второй предметной точки P2 на основной оси зрения (от точки P1 до бесконечности) угол a соответственно изменяется в пределах от 0 до значения b » r sing/H. При характерных величинах r, g и H=500 мм оценка величины угла составляет b»38¢ (это достаточно много, если учитывать дифференциальный порог разрешающей способности сетчатки, имеющий значение около 1¢, и оперативный порог различения около 10¢ [7-9]). Однако предельное значение угла a»b мало говорит о его влиянии на восприятие, поскольку разрешающая способность сетчатки неоднородна по полю и, кроме этого, необходимо оценить изменение угла a при изменении положений предметных точек и при разных углах поворота глаза (при этом проекции предметных точек попадают на разные области сетчатки, и может изменяться уровень их различе- ния [4-9]). На рисунке 4 приводятся кривые, иллюстрирующие изменение угла в зависимости от положения предметных точек P1 и P2 при разных углах поворота глаза вокруг вертикальной оси относительно основного направления зрения. Для каждой кривой точка P1 считается неподвижной, а точка P2 постепенно удаляется от нее с дистанции 1 м до бесконечности. Приведено несколько групп кривых для разных значений угла a и положений точки P1 внутри каждой группы. Значения углов выбирались из следующих соображений. На рисунке 5 схематично показано бинокулярное поле зрения, образующееся в результате перекрытия полей зрения каждого глаза (граничные значения углов для каждого поля приведены в таблице). Это поле включает участок, видимый двумя глазами одновременно (поле каждого глаза несколько шире). Область перекрытия правого и левого глаз является областью наиболее ясного видения, но внутри этой области выделяется участок в еще более узких границах (примерно в два раза [7]), внутри которого осуществляется надежное обнаружение сигнала, в частности, отклонения стрелок приборов. Одномоментная обработка информации (в пределах одной зрительной фиксации) ограничена полем, соответствующим желтому пятну размером 8° по горизонтали и 6° по вертикали [7]. Таблица Границы бинокулярного поля зрения (по [7])
При повороте глаза на угол g изображение предметной точки на сетчатке смещается на угол 2g, поэтому границам характерных зон, ограниченных по горизонтали значениями 55°, 28° и 8° (поле перекрытия, поля обнаружения и желтое пятно), будут соответствовать в два раза меньшие значения углов поворота, то есть соответственно 27.5°, 14° и 4°. К этим значениям добавлены промежуточные, и, таким образом, образован набор {27.5°, 22.5°, 14°, 8, 4°,2°} углов g, для построения групп кривых. Вид кривых говорит о многом. Во-первых, при расположении точки P1 на расстояния 1-2 м от центра проекции (зрачка) и удалении от нее точки P2 на расстояние от 1 м до 5 м происходит наиболее сильное увеличение угловой невязки. Во-вторых, угловая невязка a растет при удалении точки P2 при фиксированном положении точки P1. При этом величина невязки существенно превышает оперативный порог восприятия, составляющий 10¢ (то есть невязка хорошо различима в зоне перекрытия полей для g = 27.5 и в зоне надежного обнаружения сигнала для g= 22.5°).
Если учитывать каждое мгновенное положение оптической оси глаза, то возникают достаточно жесткие ограничения на временные рамки формирования растра изображения. Действительно, интервал времени между скачками, как правило, не превышает 0.01 секунды, но проблема в том, что для формирования изображения можно использовать далеко не весь этот интервал целиком, а лишь малую его часть, соответствующую периоду, в течение которого сетчатка еще не начала воспринимать световой поток. Исчерпывающие данные о величине этого периода отсутствуют (не исключено, что длительность его очень мала и составляет не более 10-3 секунды). Вместе с тем имеется более облегченный для реализации подход к решению возникающей задачи – использование данных не о мгновенном положении оптической оси глаза, а о дрейфе точки прицеливания. Другими словами, обновление изображения следует производить не после каждой саккады, а после серии саккад, когда угол между положениями оптической оси на краях серии саккад изменится на достаточно большую величину. Однако для решения задачи в такой постановке необходимо привлечение аппарата прогнозирования положения точки прицеливания, в том числе, с использованием калмановской фильтрации [2,3,10]. Объектная модель системы высокоточной стереовизуализации
Абстракция устройства стереовизуализации. Это устройство совмещает функции ввода данных (параметров состояния сенсорной системы оператора) и вывода данных (растра изображений стереопары), то есть является интерфейсным устройством ввода/вывода. Отображением этого устройства на программные объекты системы визуализации является виртуальный фрейм наблюдателя. Устройства, обладающие функциональностью, близкой к описанной выше, вероятно, существуют в виде экспериментальных образцов, но наиболее распространены системы HMS [11,12,14]. Вместе с тем необходимо учитывать перспективы развития технологии и технические решения, обеспечивающие сформулированные условия адекватного бинокулярного восприятия. Во всяком случае модель системы визуализации необходимо формировать с учетом таких возможностей. Рассмотрим абстракцию идеализированного устройства, позволяющего использовать расширенный набор начальных условий формирования стереопары. На рисунке 6 показан эволюционный ряд, содержащий три разновидности абстракций систем бинокулярной визуализации по возрастанию их сложности и степени приближения к наиболее полному набору функциональных возможностей. На рисунке 6(а) изображена абстракция обычного HMS-дисплея, в которой учитывается лишь положение и ориентация головы оператора, а также усредненное положение носителей растра относительно зрительных сенсоров. В конечном итоге осуществляется слежение за одной системой координат, и возможна регулировка положения и ориентации носителей растра. На рисунке 6(б) изображена абстракция более сложной системы, в которой, помимо слежения за положением всей системы, осуществляется слежение за положением и ориентацией головы (в системе координат самого устройства) и за ориентацией зрительных сенсоров (в системе координат головы). На рисунке 6(в) показана функциональная схема наиболее сложного концепт-устройства визуализации, основное отличие которого от остальных состоит в наличии специальной оптической системы, которая может в реальном времени перемещать по глубине мнимое изображение виртуальной среды, настраиваясь на мгновенное положение плоскости аккомодации, которое, в свою очередь, должно вычисляться по углу вергенции зрительных осей. Структура фрейма наблюдателя. Компоненты модели бинокулярной визуализации рассматриваются в рамках единого объекта, обладающего, в частности, свойствами координатного фрейма (поведение компонент описывается в его системе координат). Структура модели такого фрейма в обобщенном виде показана на рисунке 7. В состав фрейма включены объекты, свойства которых важны при описании начальных условий для формирования изображения проекций сцены. Заметим, что для указанных на схеме объектов лишь часть параметров состояния может быть описана непосредственно в терминах регистрирующих приборов. Другие параметры могут быть определены лишь косвенно через параметры, которые регистрируются либо являются параметрами редуцированной зрительной системы человека (общепринятой модели этой системы в терминах геометрической опти- ки [7]). Носитель растра как самостоятельный объект. Модель бинокулярной визуализации должна содержать не только описание анатомического отдела зрительного анализатора человека, но и носителей изображения, так как на условия восприятия влияет их взаимное расположение. Основным свойством носителя растра является его прозрачность. Это означает, что наблюдатель не должен ощущать присутствия носителя изображения – в худшем случае последний должен восприниматься как стекло в оконной раме, как ветровое стекло автомобиля и т.п. Для обеспечения этого свойства необходимо точное описание положения носителя относительно зрительных сенсоров и т.д. Будучи частью внешнего физического устройства, носитель представляет собой поверхность сложной формы. В ряде случаев эта поверхность визуализации может быть сегментирована, причем сегменты могут иметь различные размеры, форму и пространственное расположение. С каждым из сегментов картинной поверхности может быть сопоставлен автономный объект, выполняющий функции, сходные с функциями типовой виртуальной камеры [1]. Однако в данном случае не имеет смысла вводить такие понятия, как порт просмотра, поскольку преобразования полученного изображения (масштабирование по осям и т.п.) подчинены единой геометрической модели картинной поверхности.
Вместе с тем стереоскопическую визуализацию (точнее, визуализацию двухмерных полей стереопары), вообще говоря, следует считать полноценным и вполне адекватным подходом, поскольку рецепторное поле зрительного анализатора человека принципиально является двухмерным (сфероидальная поверхность сетчатки). Проблема состоит в том, что в широко распространенном подходе к стереоскопической визуализации не учитываются многие важные факторы, влияющие на адекватность бинокулярной визуализации как таковой. В данной работе показано, что на условия бинокулярного восприятия могут влиять вергентное смещение оптических центров глаз и связь угла вергенции с положением плоскости аккомодации. Эти факторы особенно сильно могут сказываться на небольших расстояниях (соизмеримых с глубиной зоны аккомодации) и при построении системы визуализации ИВС в ближней зоне (indoor [2,3]) их необходимо учитывать. Однако жесткие ограничения на величину временного интервала, отводимого на формирование изображения, требуют использования для этой цели высокопроизводительных вычислительных систем (на данный момент требуется уровень суперкомпьютеров). При создании систем бинокулярной визуализации виртуальной 3D-среды нового поколения необходимо использовать модель более полную по сравнению общепринятой моделью стереоголовы с 6-ю степенями свободы (6-DOF, [2,3]). Эти системы могут использоваться как средство информационной поддержки в сложных операциях, для космических, навигационных, тренажерных и других систем, в которых необходима высокоточная совмещенная визуализация реальной и виртуальной сред. Список литературы 1. Хилл Ф. OpenGL. Программирование компьютерной графики. – СПб.: Питер, 2002.- 1088 с. 2. Jiang B., You S., Neumann U. A Robust Tracking System for Outdoor Augmented Reality, IEEE Virtual Reality 2004, Chicago, pp. 3 - 10, March 27-31, 2004. 3. Lee J.W, Neumann U. Motion Estimation with Incomplete Information using Omnidirectional Vision. IEEE International Conference on Image Processing (ICIP'00), Vol. 2, pp. 562-565, Vancouver Canada, September 2000. 4. Кравков С.В. Глаз и его работа. - М.-Л.: Изд-во АН СССР. - 1950. 5. Шульговский В.В. Основы нейрофизилогии: Учебное пособие. - М.: Аспект Пресс, 2002.-277 с. 6. Марр Д. Зрение. Информационный подход к изучению представления и обработки зрительных образов.-М.: Радио и связь, 1987. 7. Литвак И.И., Ломов Б.Ф., Соловейчик И.Е. Основы построения аппаратуры отображения в автоматизированных системах. - М.: Сов. радио, 1975. 8. Степанов Б.И. Введение в современную оптику. О возможном и невозможном в оптике. - Мн.: Наука и техника, 1989.-254 с. 9. Ландсберг Г.С. Оптика. - М.: Наука, 1976. - 928с. 10. Ермаков С.М., Бродский В.З. и др. Математическая теория планирования эксперимента. – М.: Наука, 1983. – 392 с. 11. Burdea G., Coiffet P. Virtual Reality Technology. – New York: John Wiley&Sons, Inc, 1994. 12. Helsel S.K. (Ed.). Beyond the vision. The technology, research and businnes of virtual reality. Meckler, London, 1992. 13. «Жидкая линза» для мобильных устройств. – Пресс-релиз hpc.ru (10 марта, 2004 г.). 14. Катыс Г.П., Катыс П.Г., Яковлев А.И. Трехмерные системы представления объемной информации. - М.:СИП РИА, 1998. – 112 с. 15. Михайлюк М.В., Решетников В.Н., Хураськин И.А. Технология взаимодействия человека с виртуальной средой. // Программные продукты и системы. – 2004. - № 2. - С. 16-19. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=563&page=article |
Версия для печати Выпуск в формате PDF (1.31Мб) |
| Статья опубликована в выпуске журнала № 4 за 2004 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Тектология А.А. Богданова и неоклассическая теория организаций – предвестники эры реинжиниринга
- Две задачи, в решение которых внес коррективы компьютер
- Система визуализации реального времени на основе программируемых сигнальных процессоров
- Время перемещать камни
- Метод интегрированного описания топологических отношений в геоинформационных системах
Назад, к списку статей



 Вергентное смещение оптических центров. В общепринятой модели стереоголовы вергентные движения учитывается лишь частично, и информация об ориентации зрительных осей используется для задания усредненного положения точки прицеливания виртуальных камер. Основным мотивом выбора этой точки является создание комфортных условий для бинокулярного наблюдения статичного изображения 3D-среды (при неподвижной голове). Таким образом, изображения полей стереопары формируются на основе данных о положении вектора ориентации головы без учета мгновенных положений оптических осей глазных яблок, которые непрерывно меняют ориентацию – совершаются сак- кадные движения (саккадные скачки, или саккады) с интервалом фиксации осей длительностью 0.01-1 сек. [5,6]. В этой связи возникает вопрос: насколько сильно влияет на адекватность восприятия расхождение между условиями формирования и наблюдения изображений 3D-среды?
Вергентное смещение оптических центров. В общепринятой модели стереоголовы вергентные движения учитывается лишь частично, и информация об ориентации зрительных осей используется для задания усредненного положения точки прицеливания виртуальных камер. Основным мотивом выбора этой точки является создание комфортных условий для бинокулярного наблюдения статичного изображения 3D-среды (при неподвижной голове). Таким образом, изображения полей стереопары формируются на основе данных о положении вектора ориентации головы без учета мгновенных положений оптических осей глазных яблок, которые непрерывно меняют ориентацию – совершаются сак- кадные движения (саккадные скачки, или саккады) с интервалом фиксации осей длительностью 0.01-1 сек. [5,6]. В этой связи возникает вопрос: насколько сильно влияет на адекватность восприятия расхождение между условиями формирования и наблюдения изображений 3D-среды? В системах высокоточной 3D-визуализации проблема связи между положением плоскости аккомодации и углом вергенции должна решаться более радикальными средствами. На основе определения положения виртуальной плоскости аккомодации необходимо корректировать положения плоскости мнимого изображения виртуальной сцены (с появлением «жидких» линз с малым временем реакции [13] эта проблема поддается решению).
В системах высокоточной 3D-визуализации проблема связи между положением плоскости аккомодации и углом вергенции должна решаться более радикальными средствами. На основе определения положения виртуальной плоскости аккомодации необходимо корректировать положения плоскости мнимого изображения виртуальной сцены (с появлением «жидких» линз с малым временем реакции [13] эта проблема поддается решению).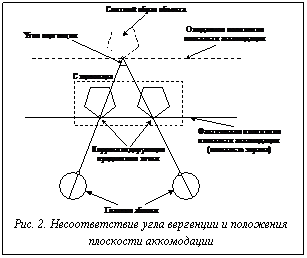 В дополнение к введенным обозначениям параметров, задающим радиус глаза, угол его поворота и положение предметных точек (соответственно, r, g, H и DH), введем обозначения параметров в соответствии со схемой на рисунке 3.
В дополнение к введенным обозначениям параметров, задающим радиус глаза, угол его поворота и положение предметных точек (соответственно, r, g, H и DH), введем обозначения параметров в соответствии со схемой на рисунке 3. Границей значений g, за которой a не превышает оперативного порога, имеет значение, близкое к 8° (a<10¢). В зоне, соответствующей желтому пятну (g=2°), угловая невязка не превышает 3¢ (характерное значение составляет от 1¢ до 2¢). Несмотря на то что эта величина меньше оперативного порога различения, она соизмерима с разрешающей способностью сетчатки (и даже превышает ее), то есть, по всей видимости, может ощущаться достаточно сильно. Таким образом, угловая невязка, возникающая из-за вергентного смещения зрачка, имеет достаточно большую величину как раз в ближней зоне наблюдения 3D-среды (от 0.5 до 3 метров) и должна учитываться при задании начальных условий формирования изображений стереопары.
Границей значений g, за которой a не превышает оперативного порога, имеет значение, близкое к 8° (a<10¢). В зоне, соответствующей желтому пятну (g=2°), угловая невязка не превышает 3¢ (характерное значение составляет от 1¢ до 2¢). Несмотря на то что эта величина меньше оперативного порога различения, она соизмерима с разрешающей способностью сетчатки (и даже превышает ее), то есть, по всей видимости, может ощущаться достаточно сильно. Таким образом, угловая невязка, возникающая из-за вергентного смещения зрачка, имеет достаточно большую величину как раз в ближней зоне наблюдения 3D-среды (от 0.5 до 3 метров) и должна учитываться при задании начальных условий формирования изображений стереопары. Основной вывод состоит в следующем. Визуальные картины, возникающие при наблюдении близко расположенных к наблюдателю объектов 3D-среды и изображений этих объектов на 2D-носителе, существенно отличаются друг от друга. Причем главной причиной такого отличия можно считать существенную разницу начальных условий проецирования самих 3D-объектов и их изображений на 2D-носителе (если не учитываются вергентные движения глаз, то эти условия совпадают).
Основной вывод состоит в следующем. Визуальные картины, возникающие при наблюдении близко расположенных к наблюдателю объектов 3D-среды и изображений этих объектов на 2D-носителе, существенно отличаются друг от друга. Причем главной причиной такого отличия можно считать существенную разницу начальных условий проецирования самих 3D-объектов и их изображений на 2D-носителе (если не учитываются вергентные движения глаз, то эти условия совпадают).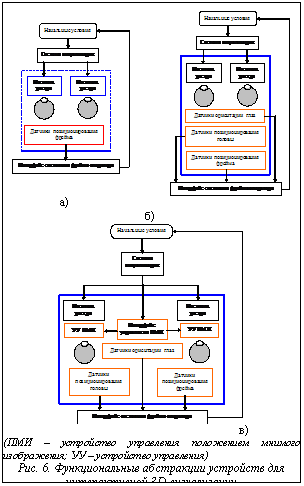 Как было отмечено, концепция стереоголовы с 6-ю степенями свободы обладает сравнительно ограниченными возможностями. В перспективных системах виртуальной реальности для обеспечения более полной функциональности видеоинтерфейса необходимо построение дополнительного «слоя» ПО, в котором виртуальная камера [1] может использоваться как низкоуровневый объект (функциональный примитив). Функции формирования начальных условий, в которых более полно учитываются особенности зрительного анализатора, должны возлагаться на многоуровневый объект с большим, чем 6, числом степеней свободы (его можно было бы назвать фрейм виртуального наблюдателя, пост визуализации и т.п.).
Как было отмечено, концепция стереоголовы с 6-ю степенями свободы обладает сравнительно ограниченными возможностями. В перспективных системах виртуальной реальности для обеспечения более полной функциональности видеоинтерфейса необходимо построение дополнительного «слоя» ПО, в котором виртуальная камера [1] может использоваться как низкоуровневый объект (функциональный примитив). Функции формирования начальных условий, в которых более полно учитываются особенности зрительного анализатора, должны возлагаться на многоуровневый объект с большим, чем 6, числом степеней свободы (его можно было бы назвать фрейм виртуального наблюдателя, пост визуализации и т.п.).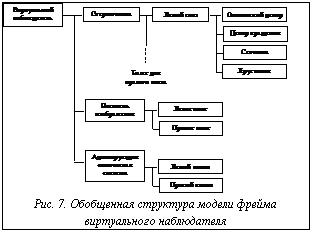 В заключение отметим, что в настоящее время не прекращается поиск подходов к 3D-визуализации, позволяющих максимально приблизить условия восприятия виртуальной 3D-среды к естественным. Справедливо считается, что идеальным является подход, в котором в 3D-пространстве можно наблюдать непосредственно сам 3D-объект [14]. Например, реализация в системах ВР принципов голографии или 3D-развертка на движущихся носителях позволили бы в большинстве случаев отказаться от стереоскопической визуализации и использования для этой цели дисплейных устройств всех существующих типов (стационарных и носимых).
В заключение отметим, что в настоящее время не прекращается поиск подходов к 3D-визуализации, позволяющих максимально приблизить условия восприятия виртуальной 3D-среды к естественным. Справедливо считается, что идеальным является подход, в котором в 3D-пространстве можно наблюдать непосредственно сам 3D-объект [14]. Например, реализация в системах ВР принципов голографии или 3D-развертка на движущихся носителях позволили бы в большинстве случаев отказаться от стереоскопической визуализации и использования для этой цели дисплейных устройств всех существующих типов (стационарных и носимых).