Разработка технологии нечеткого моделирования ситуаций принятия решений в частично формализованных системах
| Вовк С.П. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Различные организационные системы относятся к классу частично формализуемых систем. Особый интерес представляют организационные системы, состоящие из двух подсистем, которые могут действовать согласованно или конфликтно в целях достижения наилучшей (в определенном смысле) общей для системы динамики нарастания некоторого необходимого качества. Последовательное принятие решения (ПР) по управлению взаимодействием таких подсистем осуществляется с учетом ограничений в виде предыстории протекания процесса взаимодействия в условиях несовпадающих систем предпочтений. У исследуемого класса есть основные особенности организационных систем. · Оптимальную стратегию достижения глобальной цели диктует I1, которой принадлежит инициатива в выборе правил взаимодействия по причине обладания в большей степени опытом и ресурсами. Оптимальная стратегия определена желаемой динамикой нарастания необходимого качества, отражающей темп нарастания интегрального показателя качества. · Пассивная подсистема I2, которой навязываются правила взаимодействия, обладает некоторой реальной динамикой нарастания показателя качества. Сравнение темпов нарастания интегрального показателя качества у пассивных подсистем, обладающих разными характеристиками, позволяет в каждый момент функционирования определить динамически изменяющуюся принадлежность к классу. · I2 пытается достигнуть общей цели с минимумом затрат: (вступает в коалицию или антагонистически противоборствует). Нарастание показателя качества оценивается с учетом первоначального уровня сложности работ и ввиду несовпадения оценок уровней сложности исходы взаимодействия описываются интервалами. В отличие от традиционно рассматриваемых в теории игр сценариев поведения выбор стратегии взаимодействия I1 в некоторый момент ПР зависит от ранее проявленной I2 способности к накоплению качества. Способности проявляются в виде величины отклонения желаемой и реальной динамик нарастания показателя качества и определяют выбор класса стратегий для возврата к желаемой динамике. Стратегии некоторого класса моделируются соответствующим фрагментом. Необходимость учета названных особенностей приводит к тому, что в общей постановке задачи моделирования и анализа частично формализованных систем отчетливо виден ряд вспомогательных задач: 1) модель динамики нарастания необходимого качества; 2) построение ситуационной модели игры с динамически меняющимся классом стратегий активного игрока и управление ее сценарием; 3) выбор лучшей тактики противодействия по отношению к противоположной стороне с учетом множеств критериев сторон. Первая модель строится либо по результату экспертной оценки трудоемкости и значимости выполненных работ, либо оптимальная траектория определяется по описанию системы рекуррентными соотношениями Бэллмана. Для решения второй задачи требуется: · сформировать сценарий, описываемый конечным графом где · определить допустимые тактики игрока для шага ПР tj, что требует решения третьей задачи; · определить для I1 максимизирующее управление В качестве основной модели для решения третьей задачи выбрана известная теоретико-игровая модель анализа конфликтной ситуации. Путем анализа конкретной ситуации ПР, представленного на рисунке, предлагается переход от общей теоретико-игровой модели к конкретной форме матричной игры. Переход производится следующим образом: - при ситуации ПР, характеризующейся четкими исходами взаимодействия и известными вероятностями их наступления, выполняется переход к модели четкой игры Неймана-Моргенштерна [1]; - при последствиях альтернатив
где Р={Рp} – множество значений лингвистических вероятностей, каждое из которых формализуется нечетким числом с
Формализация ситуации 2 с помощью Гнч, несмотря на попытки, предпринятые в работе [2], оставляет нерешенными важные с точки зрения практики моделирования вопросы: 1) каким образом учитывается система предпочтений игрока при выборе им решения в tj, 2) Предлагается постановку задачи определения желаемого уровня достижения цели I1 в условиях наличия противодействующей стороны I2 представить в виде кортежа:
где В результате анализа подходов к учету нечеткости, возникающих из-за многих критериев, автором было выявлено, что имеющиеся процедуры учета многокритериальности при построении множества недоминируемых альтернатив Aндi i-го игрока не отражают ограниченности информации о состоянии противоположной стороны. Многокритериальность может быть учтена с использованием степени разделения возможностей агреги- рованных предпочтений игроков относительно альтернатив при разных предположениях о состоянии внешней среды. Исследование моделей, реализующих алгоритм
где Для определения желаемого уровня достижения цели hi использовано понятие “порог разделения зон” [3]:
где Аналогично может быть определен уровень для противника. Равновесное решение нечеткой игры ищется как Предложенный метод поиска равновесного решения нечеткой игры в условиях многокритериального выбора игрока и ограниченности информации о состоянии другой стороны позволил разработать технологию моделирования игровых ситуаций с исходами взаимодействия, описываемых интервалами. Основные пункты технологии моделирования ситуаций ПР с использованием четких и нечетких игр следующие. 1. Представить схему взаимодействия " I1 -I2" в виде дерева позиционной игры. 2. Выявить множества тактик A1 для I1 и A2 для I2. 3. Перейти к п. 4 при возможности однозначной оценки исходов всех партий. Перейти к п. 6 в случае неоднозначности оценки некоторых исходов, то есть исходов, оцененных преподавателем в виде нечеткого интервала [b1,b2]. 4. Определить ожидаемые выигрыши игро- ков с помощью [1] 5. Представить схему взаимодействия в матричной форме, затем осуществить поиск оптимальных решений с использованием традиционных методов решения матричных игр [1]: · при наличии "седловой точки" – с помощью · при ее отсутствии – с помощью Перейти к п. 25. 6. Упорядочить состояния, в которых может находиться I2, по убыванию их вероятностей p(c1)³ …³ p(cm) на основе ранее рассмотренной оценки вероятностей возможных состояний противоположной стороны. Оценить степень истинности утверждения a=“состояния C упорядочены по убыванию вероятности” как Т( 7. Определить нечеткие оценки полезности тактики I1 при применении альтернатив af, ag в виде [4] 8. Результат сложения нечетких чисел обозначим 9. Если Если с использованием четкого доминирования по полезности нельзя упорядочить тактики, при пересечении интервалов, перейти к п. 10, а при включении – к п. 11. 10. Если имеет место пересечение интервалов оценок полезностей, то оценить истинность утверждения zk’= можно с помощью [4] Перейти к п. 10. 11. В случае включения интервалов оценок полезностей оценить истинность утверждения Т(zk’) с помощью формулы [4]
12. В случае пересечения интервалов оценок полезностей оценить истинность Т(zk”) утверждения zk”= с помощью формулы [4] В случае включения интервалов оце- нок – с помощью формулы [4] 13. Определить степень доминирования альтернативы af над ag как 14. Определить степень доминирования альтернативы ag над af как 15. Оценить истинность утверждения T(b) [4] с помощью 16. Определить степень доминирования 17. Произвести парный анализ тактики af с другими agÎA1, выполнив п. 8-16 на множестве A1. 18. Построить нечеткое множество недоминируемых тактик AНД1 и с [4] 19. Задачу анализа тактик для I2 задать отображением a: N®W, рассматривая в качестве возможных состояний природы наборы работ xÎX. Построить нечеткое множество недоминируемых тактик AНД2 игрока I2, для чего выполнить п. 6-18 алгоритма на множестве тактик A2. 20. Выполнить попарное сравнение Wf, Wg в случае пересечения интервалов оценок с помощью Построить [4] нечеткое множество не- доминируемых тактик AНД2 с 21. Определить нечеткость исхода [2], получающегося в результате применения нечетких стратегий игроками, согласно A1´A2={((a1,a2), s1(a1) Ù s2(a2))}, где a1ÎA1 , a2Î A2. 22. Построить на нечетком множестве исходов W=A1´A2 четкие отношения уровня Rhi={(a1,a2)ÎA1´A2|R(a1,a2)³hi} (i=1,2) с использованием определенных с помощью (3) желаемых уровней I1 и I2. 23. Найти равновесное решение игры с помощью Rh=Rh1Ç Rh2, где hi – уровень нечеткого отношения R i-го игрока. Под отношением уровня понимается четкое отношение Rhi, определяемое для " hi >0 следующим образом: Rhi ={(w,w¢)Î W1´W2 |R(w,w¢)³hi }. 24. Вычеркнуть нулевые строки и столбцы в матрице отношения Rh. Исходы, оставшиеся после вычеркивания, составляют множество Парето. 25. Конец. Названная технология моделирования ситуаций ПР с использованием четких и нечетких игр получила практическую реализацию в АРМ преподавателя-исследователя, занимающегося планированием, организацией, контролем учебного процесса. При работе с АРМ преподаватель-исследователь использует основное меню с пунктами: “Работа с календарным планом”, “Работа с деревьями”, “Выход”. При выборе режима “Работа с календар- ным планом” появляется возможность выбора нужного режима работы: “Новый”, “Открыть”, “Выход”. Календарный план представляет собой последовательность контрольных занятий с заданиями разной сложности в разные моменты контроля знаний, каждое из которых моделируется деревом, характеризующим конкретного учащегося как представителя класса по обучаемости. Возможность моделирования оптимальной планируемой рейтинг-характеристики достигается за счет перераспределения баллов между точками контроля. Фактическая рейтинг-характеристика строится по результатам контроля знаний студента или группы. В режиме “Работа с календарным планом” предусмотрены возможности построения нового плана, просмотра или корректировки существующих. Возможности по редактированию календарного плана следующие. – Вставить пункт. Вводится номер эталонного дерева (при работе со стандартными эталонными деревьями) или имя файла для нового дерева, а также планируемые и фактические количества баллов и точки выхода. Для определения точки выхода курсор перемещается в ту вершину на дереве игры, которая будет точкой выхода, и нажимается клавиша Esc. - Удалить пункт плана. - Редактировать общую информацию о плане. - Редактировать текущее дерево игры (план). - Редактировать текущее дерево игры (факт). - Подсчитать фактические баллы. - Редактировать информацию о текущем пункте плана. В режиме “Работа с деревьями” экран пользователя условно разделен на 3 части: дерево – в нижней части экрана, информация – в левом верхнем углу экрана, помощь – в правом верхнем углу экрана. Каждый из узлов дерева может содержать сколь угодно большое число потомков. Количество уровней в дереве ограничено размером экрана (7 уровней). Каждый лист дерева имеет следующие параметры. 1. Выигрыш при попадании в вершину, характеризующую результат контроля (0.0, 0.6, 0.8, 1.0 от максимума). 2. Вероятность попадания в данную вершину из предыдущей. Для вершин одного уровня, имеющих общего предка, сумма вероятностей равна 1.0. Для лучшего визуального восприятия такие вершины отображаются на экране в виде белого кружка, все остальные – в виде красных. 3. Цвет связи с предыдущей вершиной облегчает понимание, для какого типа ученика предназначена данная ветвь дерева (синий – для слабого, зеленый – для среднего, красный – для сильного). 4. Вероятность конкретной партии. 5. Последовательность заданий и их уровни сложности. Игра развивается в виде одной из партий. Преподаватель выдает задания в вершинах выдачи задания, учащийся их выполняет, в вершинах принятия решения преподаватель оценивает выполнение учащимся задания. Узел выдачи задания отражает набор уровней сложности задания в дереве, номер выдаваемого задания на участке партии (проставляется автоматически), вероятность попадания в вершину из предка, цвет связи с предком, комментарий. Узел принятия решения описывается следующей информацией: выигрыш (0.0, 0.6, 0.8, 1.0), вероятность попадания из предка, цвет связи с предком, вероятность попадания в данную вершину из корня дерева, последовательность уровней сложности заданий для партии. Попадая в вершину-лист, располагаем следующей информацией: вероятность попадания в эту вершину, выигрыш, последовательность выполнения заданий. В режиме просмотра при нажатии клавиши Enter на экран выводятся матрица вероятностей исхода и матрица выигрышей. Дерево игры может редактироваться в одном из режимов: редактирование общей информации о дереве – клавиша F3, полноэкранное редактирование дерева (пользователь имеет возможность создавать новое дерево или редактировать уже существующее) – клавиша F4. В последнем режиме пользователь может выполнять следующие операции: “Добавление вершины” – клавиша Ins, “Удаление вершины” – клавиша Del, “Редактирование информации о вершине”– клавиша Enter, “Перемещение вершины (изменение координат)” – клавиша пробел (Space). Предлагаемый комплекс моделей может найти более широкое практическое применение, в частности, его возможно применять для целей дистанционного обучения (ДО). Известно, что учебные курсы, программы, информационное обеспечение для ДО разрабатываются, главным образом, на основе интуиции разработчиков и педагогического мастерства экспертов-педагогов. Наиболее перспективно формализацию описаний и анализа учебных ситуаций без упрощения их сложности производить с помощью нечетких множеств. Однако не существует комплекса моделей, позволяющих учесть ранее названную специфику взаимодействия подсистем в организационных системах. Поэтому также предложены алгоритмы построения сценария игры и определения максимизирующего управления в сценарии, часть исходов которого описывается нечеткими интервалами. Их особенности заключаются в следующем. Алгоритм построения сценария игры включает дополнительный этап построения дерева управляющих решений с учетом последовательности работ с разным начальным уровнем сложности. Использование максимизирующего управления в нечеткой ситуационной сети позволяет достигать желаемую цель с удовлетворяющей ЛПР возможностью или корректировать первоначально запланированную цель с учетом текущей классификации пассивной подсистемы. На основании этих алгоритмов разработаны технологии построения сценария игры и определения максимизирующего управления в ситуационной сети, позволяющие организовывать нужную динамику нарастания показателя качества у системы в целом. Использование нечетких ситуационных моделей для управления взаимодействием игроков позволяет устранить один из главных недостатков матричной игры – отсутствие динамичности, и дает возможность при выборе решения в сложной системе учесть интуитивные действия ЛПР. Список литературы 1. Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. - М.: Наука, 1970. –340 с. 2. Ragade R.K. Fuzzy games in the analysis of options Journal of Cubernetics, 1976, v.6, h.213-221. 3. Леунг Й. Разделение на торговые зоны в нечетких условиях: Теория возможностей и ее применение. - М.: Наука, 1992. –272 с. 4. Обработка нечеткой информации в системах принятия решений // А.Н. Борисов, А.В. Алексеев, Г.В. Меркурьева и др. - М.: Радио и связь, 1989. –304 с. |
http://swsys.ru/index.php?id=579&lang=.docs&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Эвристические и точные методы программной конвейеризации циклов
- Макроэкономическая балансовая модель для стран с элементами переходной экономики
- Параллельная обработка в алгоритмах визуализации с трассировкой лучей
- Формирование программ развития больших систем административно-организационного управления
- Формулировка задачи планирования линейных и циклических участков кода

 = (Ss, V),
= (Ss, V), представляет собой объединение всех эталонных ситуаций
представляет собой объединение всех эталонных ситуаций  моментов управления tj, j=
моментов управления tj, j= ; VÍSs´Ss описывает переходы между эталонными ситуациями разных tj с помощью отображений множества эффективных (или оптимальных) тактик игрока I1 в множество дуг
; VÍSs´Ss описывает переходы между эталонными ситуациями разных tj с помощью отображений множества эффективных (или оптимальных) тактик игрока I1 в множество дуг  и полезностей этих тактик в множество дуг
и полезностей этих тактик в множество дуг  ;
; с
с 
 для попытки возврата I2 к запланированной динамике нарастания качества в условиях существования ограничения на силу воздействия в виде предыстории
для попытки возврата I2 к запланированной динамике нарастания качества в условиях существования ограничения на силу воздействия в виде предыстории  ;
;  и допустимости найденного решения
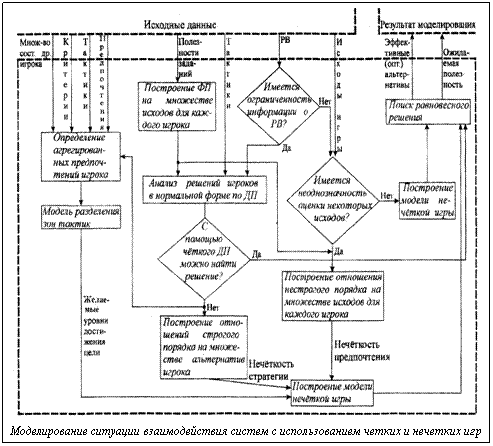
и допустимости найденного решения  , формализуемых
, формализуемых 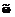 с функцией полезности (ФП)
с функцией полезности (ФП)  , и ограниченности информации о вероятностях исходов (РВ)
, и ограниченности информации о вероятностях исходов (РВ)  задача ПР для игрока I1 описывается кортежем
задача ПР для игрока I1 описывается кортежем , (1)
, (1) :[0,1]®[0,1]. Последствия решений I1 оценивает по лингвистическому критерию
:[0,1]®[0,1]. Последствия решений I1 оценивает по лингвистическому критерию  . С позиций I1 задача анализа решений в нормальной форме описывается
. С позиций I1 задача анализа решений в нормальной форме описывается  . Структура предпочтения I1 представляет бинарное нечеткое отношение нестрогого доминирования
. Структура предпочтения I1 представляет бинарное нечеткое отношение нестрогого доминирования  по полезности (ДП). Принцип выбора элементов из A1(tj) на основе результата парного сравнения альтернатив состоит в построении Rs1(tj) с
по полезности (ДП). Принцип выбора элементов из A1(tj) на основе результата парного сравнения альтернатив состоит в построении Rs1(tj) с  .
. определяет нечеткость тактики с нечетким подмножеством недоминируемых тактик (эффективных решений) с
определяет нечеткость тактики с нечетким подмножеством недоминируемых тактик (эффективных решений) с  . Это преобразование описывает модель нечеткой игры
. Это преобразование описывает модель нечеткой игры  , где
, где  – тактики i-го игрока;
– тактики i-го игрока;  – бинарные нечеткие отношения нестрогого предпочтения i-го игрока на множестве
– бинарные нечеткие отношения нестрогого предпочтения i-го игрока на множестве .
. каким образом выбирается желаемый уровень достижения
каким образом выбирается желаемый уровень достижения  промежуточной цели
промежуточной цели  .
. , (2)
, (2) – система предпочтений, под которой понимается совокупность представлений лица, принимающего решения (ЛПР), в момент tj о критериях
– система предпочтений, под которой понимается совокупность представлений лица, принимающего решения (ЛПР), в момент tj о критериях  и достоинствах тактик для представителей разных классов I2, задаваемых в виде отображения
и достоинствах тактик для представителей разных классов I2, задаваемых в виде отображения  ;
;  – алгоритм, позволяющий определить же- лаемый уровень
– алгоритм, позволяющий определить же- лаемый уровень  достижения цели на множестве агрегированных предпочтений
достижения цели на множестве агрегированных предпочтений  ;
;  заключается в процедуре построения уровня h1 нечеткого
заключается в процедуре построения уровня h1 нечеткого  , которое необходимо представить в виде функциональной зависимости
, которое необходимо представить в виде функциональной зависимости  .
. на матрице агрегированных предпочтений
на матрице агрегированных предпочтений  , показало, что для определения hi – уровня различения альтернатив игрока Ii можно воспользоваться понятием “порог разделения зон” альтернатив, введенным в общей модели “разделения торговой зоны” Й. Леунга [3]. С учетом названного для |
, показало, что для определения hi – уровня различения альтернатив игрока Ii можно воспользоваться понятием “порог разделения зон” альтернатив, введенным в общей модели “разделения торговой зоны” Й. Леунга [3]. С учетом названного для | | определяется
| определяется ,
, – степень совместности тактики am с критерием l;
– степень совместности тактики am с критерием l;  – степень важности для представителя класса c противника Крите- рия l с точки зрения рассматриваемого в игре класса Ii.
– степень важности для представителя класса c противника Крите- рия l с точки зрения рассматриваемого в игре класса Ii. , (3)
, (3) – агрегированные предпочтения рассматриваемого в игре класса Ii относительно тактик
– агрегированные предпочтения рассматриваемого в игре класса Ii относительно тактик  для представителей класса c противника.
для представителей класса c противника. [2]. Оно выделяет на W область W¢ удовлетворительных исходов. Стратегии игроков, соответствующие w(a1,a2)ÎW¢, представляют эффективные решения игроков при выборе первой альтернативы I1 и второй альтернативы I2. W¢ служит основой для поиска единственного управления для I1, отвечающего требованию достижимости промежуточной цели для представителей класса c игрока I2. Для нахождения единственного управления был разработан алгоритм определения максимизирующего управления для очередного шага ПР.
[2]. Оно выделяет на W область W¢ удовлетворительных исходов. Стратегии игроков, соответствующие w(a1,a2)ÎW¢, представляют эффективные решения игроков при выборе первой альтернативы I1 и второй альтернативы I2. W¢ служит основой для поиска единственного управления для I1, отвечающего требованию достижимости промежуточной цели для представителей класса c игрока I2. Для нахождения единственного управления был разработан алгоритм определения максимизирующего управления для очередного шага ПР.
 , где функция выигрыша Gi является показателем успеха игрока на множестве исходов
, где функция выигрыша Gi является показателем успеха игрока на множестве исходов ,
, , где a1,a2 – чистые стратегии игроков I1 и I2 соответственно;
, где a1,a2 – чистые стратегии игроков I1 и I2 соответственно;  – смешанные стратегии; G(a1,a2),
– смешанные стратегии; G(a1,a2),  – математическое ожидание выигрыша в чистых и смешанных стратегиях.
– математическое ожидание выигрыша в чистых и смешанных стратегиях. )=1.
)=1. и
и  , u,vÎ[0,1] для всех k возможных состояний противоположной стороны.
, u,vÎ[0,1] для всех k возможных состояний противоположной стороны. ,
,  с функциями принадлежности
с функциями принадлежности  ,
,  , определяемыми [4]
, определяемыми [4]  и
и  .
. , то принять mД (ag,af)=0 "agÎA1 и перейти к п. 17.
, то принять mД (ag,af)=0 "agÎA1 и перейти к п. 17. .
. .
. .
.
 .
. , где
, где  определена в п. 10 или 11.
определена в п. 10 или 11. , где
, где  определена в п.12.
определена в п.12. .
. с помощью характеристической функции отношения ДП [4]
с помощью характеристической функции отношения ДП [4]  .
. .
. , а в случае включения интервалов оценок с помощью
, а в случае включения интервалов оценок с помощью  .
.
 .
.