Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Математическая модель управления процессом эпидемии в двух социальных группах
Аннотация:
Abstract:
| Авторы: Андреева Е.А. (natmat68@mail.ru) - Тверской государственный университет, доктор физико-математических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 17252 |
Версия для печати Выпуск в формате PDF (1.24Мб) |
На современном этапе развития науки и техники большое внимание уделяется математической теории оптимального управления, позволяющей находить решения сложных прикладных задач с помощью методов математической теории оптимального управления. Одной из таких задач является задача о распространении эпидемии в неоднородном сообществе, контролируемая проведением вакцинации восприимчивых к заболеванию людей и карантина. Особенностью данной модели является учет вероятности заболевания при встрече инфицированного и подверженного заболеванию человека и латентного периода заболевания. Модель описывается системой интегро-дифференциальных уравнений типа Вольтерра. В работе аппарат математической теории оптимального управления использован для исследования процессов распространения заболевания. Среди моделей, рассмотренных в [1-5], можно выделить модели эпидемии в однородном и неоднородном сообществах. Наиболее распространенными противоэпидемическими средствами являются вакцинация населения, подверженного заболеванию, и медикаментозное лечение инфицированных людей. При некоторых тяжелых заболеваниях контроль за ходом эпидемии осуществляется с помощью изоляции инфицированных людей. Другим методом контроля является проведение программы "Здоровье", которая состоит в организации теле- и радиопередач, лекций, посвященных этой проблеме, и т.д. Эти меры можно рассматривать в качестве управляющих воздействий на ход эпидемии. Обсудим две модели эпидемии в неоднородном сообществе, состоящем из двух социальных групп. Модели учитывают наличие иммунитета (постоянного или временного), факторы естественной рождаемости и смертности, латентный период заболевания и другие параметры. Модель процесса распространения эпидемии в двух социальных группах, описываемая системой обыкновенных дифференциальных уравнений Введем следующие обозначения: T – фиксированное время, на котором рассматривается процесс распространения заболевания; X(t), x(t) – численность населения, восприимчивого к заболеванию в 1-й и 2-й социальных группах соответственно в момент времени t; Y(t), y(t) – численность инфицированного населения в 1-й и 2-й социальных группах соответственно в момент времени t; γ‾¹ – коэффициент, характеризующий время естественного выздоровления, которое может изменяться от 10 дней в случае ангины и гриппа до нескольких недель в случае холеры. Предполагается, что заболевание передается только при встрече восприимчивого к заболеванию человека с инфицированным. Коэффициент β1 характеризует скорость заражения людей в 1-й социальной группе в результате встреч с инфицированными людьми из этой же группы, β2 – соответствующий коэффициент для 2-й группы, коэффициент δ1 характеризует скорость заражения людей в 1-й социальной группе в результате встреч с инфицированными людьми из 2-й группы, коэффициент δ2 характеризует скорость заражения людей во 2-й группе в результате встреч с инфицированными людьми из 1-й группы. Управление эпидемией осуществляется с помощью вакцинации восприимчивого к заболеванию населения и карантина:
Процесс распространения заболевания на отрезке времени [0,T] в двух социальных группах описывается системой нелинейных дифференциальных уравнений:
с начальными условиями:
Затраты на проведение вакцинации и карантина в каждой группе ограничены:
Цель управления эпидемией состоит в минимизации функционала J(v,u), который включает затраты на лечение инфицированных людей, затраты на проведение вакцинации и карантина во всех социальных группах. Принимая стоимость лечения одного больного за единицу, запишем общую стоимость эпидемии за время T:
где ci – относительная стоимость карантина в i-й социальной группе; di – относительная стоимость вакцинации в i-й социальной группе; i=1,2. Запишем функцию Понтрягина:
введем функции переключения:
Теорема. Пусть процесс
а сопряженные функции описываются системой дифференциальных уравнений:
с граничными условиями:
Модель распространения эпидемии с учетом распределенного запаздывания Инфекционное заболевание передается только при встрече восприимчивого к заболеванию и инфицированного человека. Вероятность заболевания вследствие контакта зависит от иммунитета человека, проводимых им профилактических мер безопасности и т.д. Инкубационный период заражения человека, в который болезнь развивается внутри организма и не имеет внешних проявлений, в каждом отдельном случае имеет свое значение. Учет этих факторов в исходной модели при описании динамики процесса осуществляется с помощью системы интегро-дифференциальных уравнений типа Вольтерра:
Функция G(t,s) характеризует влияние числа встреч инфицированных и восприимчивых к заболеванию людей в момент времени s на процесс передачи инфекции в момент времени t. На данную функцию наложен ряд ограничений, а именно:
В работе выбирается функция G(t,s) следующего вида:
Задача оптимального управления состоит в минимизации функционала (5) при ограничениях (3), (4), (11). Запишем функцию Понтрягина:
Теорема (необходимые условия оптимальности). Пусть процесс
Сопряженные функции описываются системой интегро-дифференциальных уравнений:
На правом конце отрезка интегрирования выполняются условия трансверсальности:
Для реализации численных методов используется правило левых прямоугольников для вычисления интеграла и схема Эйлера для аппроксимации производных. Дискретная задача оптимального управления имеет вид:
Задача оптимального управления решена методом проекции градиента при следующих параметрах. За единицу времени принят один месяц, за единицу стоимости – стоимость лечения одного инфицированного больного; ε=10-7 (точность вычислений); α=130, β=0,0001 (коэффициенты функции G(t,s)); T=10 (время распространения заболевания); q=1000 (число точек разбиения отрезка); di=0,0002 у.е. (стоимость проведения вакцинации в i-й социальной группе); ci=0,001 у.е. (стоимость проведения карантина в i–й социальной группе); i=1,2; γ=1 (скорость естественного выздоровления); uiº=0 (доля людей на карантине в начальный момент времени); viº=0 (интенсивность проведения вакцинации в начальный момент времени); Xº=500000 человек в 1-й социальной группе, подверженных заболеванию; xº=250000 человек во 2-й социальной группе, подверженных заболеванию; Yº=37 инфицированных человек в 1-й социальной группе; yº=50 инфицированных человек во 2-й социальной группе; Umax1=0,8, Umax2=0,7 (правое ограничение на проведение карантина в обеих группах); Vmax1=15000, Vmax2=5000 (правое ограничение на проведение вакцинации в обеих группах); β1=0,000002; δ1=0,000001; β2=0,000002; δ2=0,000002 (частота встреч инфицированных и восприимчивых к заболеванию людей из разных социальных групп). Результаты расчета выводятся в виде таблицы и графиков. Список литературы 1. Андреева Е.А. Оптимальное управление динамическими системами. - Тверь: ТвГУ, 1999. 2. Андреева Е.А., Бенке X. Оптимизация управляемых систем. - Тверь: ТвГУ, 1996. 3. Андреева Е.А., Семыкина Н.А. Оптимальное управление. - Тверь: ТвГУ, 2003. 4. Семыкина Н.А. Линейная задача оптимального управления с фазовыми ограничениями // Оптимальное управление динамическими системами: Сб. науч. тр. - Тверь: ТвГУ. - 2001. С. - 72-88. 5. Behncke H. The control of deterministic epidemics// Math. Appl. Sci. 1993. V.3. P. 298-311. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=586&page=article |
Версия для печати Выпуск в формате PDF (1.24Мб) |
| Статья опубликована в выпуске журнала № 3 за 2004 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Спецификация объектно-ориентированной модели данных с помощью отношений
- Средства обеспечения надежности функционирования информационных систем
- Кросс-система автоматизации разработки программного обеспечения на базе языка высокого уровня Рада
- Функционально-информационные модели бухгалтерского учета
- Прототип интеллектуальной системы поддержки принятия решений для управления энергообъектом
Назад, к списку статей



 – скорость введения вакцины в i-й социальной группе в момент времени t,
– скорость введения вакцины в i-й социальной группе в момент времени t, – доля людей, отправленных на карантин в i-й социальной группе в момент времени t, i=1,2.
– доля людей, отправленных на карантин в i-й социальной группе в момент времени t, i=1,2. (1)
(1) . (2)
. (2)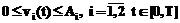 ; (3)
; (3) . (4)
. (4) (5)
(5) (6)
(6)
 является оптимальным. Тогда оптимальное управление удовлетворяет условиям:
является оптимальным. Тогда оптимальное управление удовлетворяет условиям: (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11)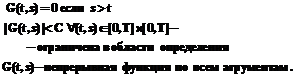
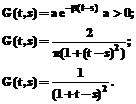
 (12)
(12) является оптимальным в задаче (3)-(5), (11). Тогда оптимальное управление находится из условий:
является оптимальным в задаче (3)-(5), (11). Тогда оптимальное управление находится из условий: (13)
(13) (14)
(14)

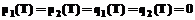 .
.