Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная поддержка процессов формирования, извлечения и проектирования баз знаний робастных интеллектуальных систем управления
Аннотация:
Abstract:
| Авторы: Язенин А.В. () - , Ульянов С.С. () - , Панфилов С.А. () - , Литвинцева Л.В. (a.mishin@ntpdubna.ru) - Университет природы, общества и человека «Дубна», г. Дубна, кандидат физико-математических наук, Такахаши К. () - , Ульянов И.С. () - , Хагивара Т. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15880 |
Версия для печати Выпуск в формате PDF (1.54Мб) |
Интеллектуальные системы управления (ИСУ), основанные на новых типах вычислений (мягкие, квантовые и т.п.), привлекают все большее внимание. Исследования показывают, что они обладают следующими достоинствами: - сохраняют главные преимущества традиционных систем управления (устойчивость, управляемость, наблюдаемость и т.п.), что составляет основу для технологии проектирования ИСУ; - имеют оптимальную (с точки зрения заданного критерия качества управления) базу знаний (БЗ), а также возможность ее коррекции и адаптации к изменяющейся ситуации управления; - гарантируют достижимость требуемого качества управления на основе спроектирован- ной БЗ; -
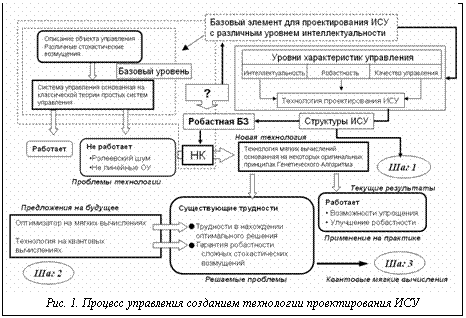
В данной статье приводятся результаты применения разработанного программного комплекса оптимизации робастных БЗ ИСУ на основе мягких вычислений. История развития ИСУ и их типовые структуры Эволюция развития и основные этапы тех- нологии проектирования ИСУ отражены на рисунке 1, а типовые структуры ИСУ приведены на рисунках 2 и 3. Исследуя задачи управления существенно нелинейными и глобально неустойчивыми объектами управления (ОУ) при наличии различных типов стохастического воздействия на ОУ (используя множество так называемых benchmarks) с помощью разработанной нами системы стохастического моделирования, мы определили предельные возможности классических систем управления (СУ), основанных на традиционном ПИД-регуляторе (рис. 2 блок 1). В результате проведенного исследования был установлен следующий факт: классические СУ, основанные на ПИД-регуляторе с постоянными коэффициентами усиления, часто не справляются с задачей управления в случае глобально неустойчивых и существенно нелинейных ОУ, находящихся под воздействием негауссовского стохастического шума. Этот факт объясняется следующими обстоятельствами. Классические СУ основаны на принципе глобальной отрицательной обратной связи и методе компенсации ошибки управления. Однако в сложных ОУ (упомянутых выше) недостаточно иметь критерий качества управления только по ошибке управления. На практике при проектировании ИСУ сложными ОУ возникает следующая проблема: как ввести в систему управления другие, дополнительные критерии качества управления, например минимум производства энтропии в ОУ, и/или минимум производства энтропии в самой системе управления (учитывающие тепловые потери и потери полезной работы в объекте и системе управления), или более сложный, векторный критерий управления. Разрешить этот вопрос с помощью процесса проектирования стандартного ПИД-регулятора с постоянными коэффициентами усиления практически невозможно.
На рисунках 2 и 3: m(t) – стохастическое воздействие, K – вектор коэффициентов усиления ПИД-регулятора, e – ошибка управления, u* – управляющие воздействие. Первое поколение ИСУ представляло собой нечеткие экспертные системы, в которых основную роль играла построенная с помощью человека-экс перта БЗ для системы нечеткого вывода. Однако в случае управления глобально неустойчивыми и существенно нелинейными ОУ, находящимися под воздействием сложных стохастических шумов, даже опытному человеку-эксперту трудно подобрать оптимальную (с точки зрения качества управления) БЗ НК. Эта проблема – узкое место всех первых (и их последующих модификаций) ИСУ [2]. Таким образом, использование экспертных систем в качестве инструментария извлечения и формирования БЗ (как основы технологии проектирования ИСУ) не привело к ожидаемому успеху (хотя существует масса примеров промышленного внедрения) в силу сложности ОУ и субъективности информации эксперта. Основной проблемой внедрения ИСУ первого поколения являлась их слабая адаптивность к изменениям параметров объекта управления (вызванных, например, старением), а также низкая робастность полученных законов управления. Для решения подобных проблем были разработаны ИСУ второго поколения, использующие так называемые мягкие вычисления, объединяющие собой генетические алгоритмы (ГА), нечеткие нейронные сети (ННС) и нечеткие регуляторы. Это позволило исключить субъективное мнение эксперта на этапе формирования структуры и параметров БЗ НК. В свою очередь, развитие ИСУ, основанных на мягких вычислениях, породило несколько подходов к структурам формирования баз знаний. Первоначально планировалось, что, получая некоторый достаточно огрубленный обучающий сигнал (ОС) от ГА, можно извлечь БЗ путем аппроксимации полученного ОС ННС. Структура ИСУ второго поколения представлена путем введения в структуру ИСУ первого поколения блока 3, включающего в себя ГА и ННС (рис. 2). В дальнейшем второе поколение ИСУ стало использовать новый вид обратной связи, называемой интеллектуальной обратной связью (ИОС) [5], представленной на рисунке 3. Ее использование дает возможность извлекать объективные знания из самого динамического поведения ОУ. Контур ИОС включает ГА для получения информации об оптимальном сигнале управления (исходя из динамического и термодинамического поведения самого ОУ) и ННС, аппроксимирующую данный оптимальный сигнал управления с помощью некоторой структуры нейронной сети. Основным блоком в структуре ИСУ (рис. 3) является система моделирования оптимального сигнала управления (СМОСУ) с помощью ГА и критерия качества управления, заданного в виде одной из составляющих вектор-функции пригодности ГА. Выходом СМОСУ является ОС (оптимального управления) в виде следующих входных/выходных данных: {E(ti), K(ti)}, i=1,…,n, где E(ti)={e(ti), Используя ОС и механизм супервизорного обучения ННС, основанный на методе обратного распространения ошибки, мы можем построить БЗ НК, представленного данной ННС. Этот этап рассматривается как шаг 1 на рисунке 1. Основной проблемой, решаемой ИСУ второго поколения с ИОС, является достижение робастности на заданном классе как параметрических, так и внешних возмущений. Моделируя поведение ОУ из множества выбранных типовых нелинейных осцилляторов, мы исследовали предельные возможности этапа 1 и установили, что в случае неустойчивых и существенно нелинейных ОУ и при воздействии на них рэлеевского стохастического шума, не удается в общем случае построить робастную БЗ, используя только этап 1 технологии построения БЗ ИСУ. Основным недостатком данного этапа является неоптимальный выбор структуры ННС соответствующей ОС. Как правило, в системах проектирования БЗ ИСУ такого типа, построение соответствующей структуры возложено на опытного человека-эксперта. ОС разделен на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В общем виде каждый из участвующих сигналов является выбранной траекторией некоторого случайного процесса. При этом подразумевается, что в каждый момент времени существует некоторая зависимость между входными и выходными сигналами. Например, в случае аппроксимации некоторого управляющего сигнала входными компонентами могут являться ошибка управления и ее производная, а выходным компонентом – требуемое значение управляющего воздействия либо некоторые настраиваемые параметры СУ (например, коэффициенты усиления ПИД-регулятора).
Другой важной проблемой является определение требуемого соотношения между точностью описания (аппроксимации) ОС и необходимой робастностью всей структуры ННС. Обе указанные проблемы решаются нами на втором этапе технологии построения БЗ ИСУ с помощью оптимизатора БЗ (ОБЗ). Структура ОБЗ ОБЗ является новым эффективным инструментом построения робастных БЗ ИСУ на основе мягких вычислений с использованием новых критериев оптимизации (в виде новых типов функций пригодности ГА). В качестве таковых мы используем термодинамические и информационно-энтро пийные критерии [1], представленные в таблице 1. ОБЗ ИСУ [6-9] (рис. 3) состоит из взаимосвязанных ГА (ГА1, ГА2, ГА3), оптимизирующих отдельные части БЗ. Входом ОБЗ является ОС, который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально непосредственно из физической модели ОУ. Последовательность реализации этапов построения ОБЗ такова. Специфицируем шаги алгоритма оптимизации. Шаг 1: выбор модели нечеткого вывода. Пользователь определяет тип нечеткой модели вывода (Сугено, Мамдани и т.д.) и число входных и выходных переменных. Шаг 2: создание лингвистических переменных. С помощью ГА1 определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее функций принадлежности (треугольная, гауссовская и т.д.). Шаг 3: создание базы правил. На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии со следующими двумя критериями: 1) выбрать только те правила, которые удовлетворяют условию: где TL (threshold level) – заданный (вручную или выбранный автоматически) уровень активации правила и 2) выбрать только те правила, которые удовлетворяют условию: Шаг 4: оптимизация базы правил. С помощью ГА2 оптимизируются правые части правил БЗ, определенной на шаге 3. На данном этапе мы находим решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС). С помощью следующего шага это решение может быть локально улучшено. Шаг 5: настройка базы правил. С помощью ГА3 оптимизируются левые и правые части правил БЗ, то есть подбираются оптимальные (с точки зрения минимума ошибки аппроксимации ОУ) параметры функций принадлежности входных/выходных переменных. При этом ГА3 в процессе оптимизации использует различные функции пригодности, выбранные пользователем (шаги 5-1, 5-2). На данном этапе имеется также возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки (шаг 5-3). Верификация (тестирование) построенной БЗ. Построенные на этапах 4,5-1,5-2 и 5-3 БЗ ИСУ тестируются с точки зрения робастности и качества управления. Для дальнейшего использования выбирается лучшая БЗ, которая апробируется в режиме функционирования в реальном времени. Программная реализация ОБЗ ОБЗ реализован в виде программной системы. В качестве языка программирования при реализации данной системы был выбран С++ (Microsoft Visual Studio.net). Алгоритмическая часть, отвечающая за выполнение основных алгоритмов оптимизации, была выполнена платформо независимо. Графический интерфейс, представленный на рисунке 4, разработан для операционных систем семейства Win32 и был опробован на компьютерах с различными установленными версиями операционной системы Windows. Главное меню оптимизатора разделено на несколько секций (рис. 4), отвечающих за выполнение основных функций и визуализацию результатов работы алгоритмов. В левой секции расположена группа кнопок, запускающих различные оптимизирующие компоненты: создание лингвистических переменных (‘Create variables’) с помощью ГА1, алгоритм генерации предикатной части нечетких правил В центральной секции главного меню оптимизатора располагается основная информация о создаваемой нечеткой системе: ее тип, адрес основного файла БЗ, число входных и выходных переменных, а также общая информация об обучающем сигнале. В центральной секции по средствам табуляторных элементов управления, расположены также редактор лингвистических переменных и редактор правил.
В нижней части главного меню оптимизатора располагается окно вывода системных сообщений, в котором дублируются параметры алгоритмов и все совершенные пользователем действия. Выводится постоянно обновляемый результат нечеткого вывода вместе с аппроксимируемым ОС. Любые действия по изменению параметров проектируемой БЗ вызывают обновление результатов аппроксимации. Таким образом пользователь визуально контролирует влияние изменения параметров БЗ на результат аппроксимации. При проектировании данной системы изначально планировалось ее совместное использование с системой Матлаб. В связи с этим был разработан интерфейс коммуникации между оптимизатором и системой Матлаб, позволяющий более гибко строить функций пригодности ГА. При этом наряду с обучающим сигналом используются результаты численного интегрирования моделей ОУ, выполненных в среде Simulink, управляемых нечеткими регуляторами, синтезированными ОБЗ. Был разработан подход, позволяющий вычислять функции пригодности в системе Матлаб с последующей передачей результатов ГА оптимизатора. Для этого была разработана соответствующая библиотека блоков среды Simulink, отвечающая за загрузку БЗ и нечеткий вывод (в режиме моделирования), а также за коммуникацию с оптимизатором (в режиме оптимизации). Блок нечеткого вывода для среды Simulink был написан также на языке С++ в виде соответствующей s-функции Simulink. Для моделирования нечеткого вывода (без использования моделей Simulink) был подготовлен соответствующий mex-файл, позволяющий получать результаты нечеткого вывода с помощью командной строки и исполняемых скриптов системы Матлаб. Программа совместима с системой Матлаб версии 6.1 и выше. Рассмотрим результаты моделирования робастных законов управления для интеллектуальных нечетких ПИД-регуляторов сложными нелинейными динамическими объектами управления на примере осциллятора, представляющего собой самостоятельный интерес для задач робототехники и механики (например, стробоскопический робот-манипулятор со сложной нелинейной динамикой поведения). Приведем сравнение результатов управления стохастическим движением ОУ для трех случаев проектирования систем управления: на основе классических ПИД-регуляторов; на основе традиционных мягких вычислений (с помощью структуры ННС, выбранной вручную, и метода построения БЗ на основе алгоритма обратного распространения ошибки) и на основе разработанного ОБЗ.
Физическая модель маятника с переменной длиной показана на рисунке 5. Уравнения движения маятника имеют вид:
где x1, x2 – соответствующие стохастические воздействия. Уравнения скорости производства энтропии имеют вид:
На приводимых ниже рисунках используются следующие обозначения: X: angle – угол; Y: length – длина; Time (S) – время (секунды); Free motion – свободное движение; unstable motion – неустойчивое движение; PID – ПИД; FNN – ННС; SCO – ОБЗ; Refsignal – задающий сигнал. Движение системы, описываемой уравнениями (1), представляет собой глобально неустойчивую (по оси l) динамическую систему (рис. 6).
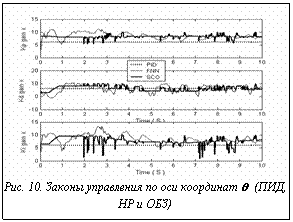
Построим ИСУ, представляющую собой нечеткий контроллер, для двух ПИД-регуляторов вдоль осей координат q и l. На рисунках 7-11 показаны результаты моделирования управления движением системы в трех случаях управления: с помощью двух классических ПИД-регуляторов (с коэффициентами усиления K={6,6,6}; на основе традиционных мягких вычислений (с помощью структуры ННС, выбранной вручную, и метода построения БЗ на основе алгоритма обратного распространения ошибки) и на
Исследование робастности ИСУ Исследуем теперь свойство робастности построенных БЗ для трех вышеприведенных случаев управления.
Задача управления с новыми условиями 1: • новые начальные данные [-0.52 (-30°), 2.5] [0.01, 0]; • новые задающие сигналы: • другие шумы, воздействующие на ОУ: - гауссовский шум вдоль оси q (максимальная амплитуда шума равна 1.5), - рэлеевский шум вдоль оси l (максимальная амплитуда шума равна 1). На рисунках 12-17 показаны результаты моделирования управления движением системы в трех случаях управления в новых условиях.
Полученные результаты моделирования позволяют сделать следующий вывод: БЗ ИСУ, разработанная с помощью традиционных мягких вычислений, не является робастной. БЗ ИСУ, разработанная с помощью ОБЗ, робастна и эффективна с точки зрения заданного критерия качества управления.
Как отмечалось, за счет интеграции с системой Матлаб ОБЗ позволяет вводить дополнительные критерии качества управления, не изменяя исходного кода программных модулей системы. В силу отмеченных выше преимуществ ОБЗ составляет основу для первого этапа технологии проектирования ИСУ.
В этом случае квантовый оптимизатор, использующий методы квантовых вычислений, в качестве исходной информации использует БЗ, спроектированные на основе ОБЗ. Это означает, что ОБЗ позволяет создавать основу для реализации второго этапа технологии, использующего квантовые вычисления. С этой целью в архитектуре ОБЗ предусмотрен программно встраиваемый интерфейс с блоком квантовых вычислений. Таким образом, перспективная информационная технология проектирования структур робастных ИСУ является двухуровневой. Первый уровень основан на ОБЗ, второй – на квантовых вычислениях. Представленные в статье методы разработки и технология проектирования ИСУ на основе ОБЗ позволяют осуществить принцип проектирования оптимальной ИСУ с максимальным уровнем надежности и управляемости сложным ОУ в условиях неопределенности исходной информации, а также при наличии стохастических шумов различной физической и статистической природы. БЗ, сформированные на основе ОБЗ, вырабатывают робастные законы управления коэффициентами усиления традиционных регуляторов для широкого диапазона внешних возмущений и максимально нечувствительны к случайным изменениям структуры ОУ. Робастность законов управления достигается введением векторной функции пригодности ГА, одна из компонент которой описывает физический принцип минимума производства скорости энтропии как в ОУ, так и в системе управления, а другая компонента описывает минимум ошибки управления и т.п. Подход, основанный на использовании ОБЗ для проектирования робастных ИСУ, позволяет: 1) проектировать оптимальную интеллектуальную систему управления с максимальным уровнем надежности и управляемости для множества динамических систем при наличии неопределенности в начальной информации [6-9]; 2) уменьшать число датчиков как в контуре каналов управления, так и в самой измерительной системе без потери точности и качества управления [14]. Кроме того, робастная ИСУ, полученная на основе такого подхода, требует минимума исходной информации как о поведении ОУ, так и о внешних возмущениях [14]. Авторы глубоко признательны профессору Ульянову С.В. за постановку задачи и полезное обсуждение результатов работы. Список литературы 1. Петров Б.Н., Уланов Г.М., Гольденблат И.И., Улья- нов С.В. Теория моделей в процессах управления: Информационные и термодинамические аспекты. - М.: Наука, 1978. 2. Петров Б.Н., Уланов Г.М., Гольденблат И.И., Улья- нов С.В. Информационно-семанти ческие проблемы процессов управления и организации систем. - М.: Наука, 1977. 3. Захаров В.Н., Ульянов С.В. Нечеткие промышленные системы управления и регуляторы. - Ч. 1-4 // Изв. АН СССР. Техн. киберн. – 1992. - № 5; 1993. - № 3, 4; 1994. - № 5. 4. Алиев Р.А., Ульянов С.В. Нечеткие модели процессов и систем управления. // Итоги науки и техники. Сер. Техн. киберн. – 1990. - Т. 29; 1991. - Т. 32. 5. US patent N 6,411,944 B1, 1997. Self-organizing control system (Inventor: S.V. Ulyanov). 6. Panfilov S. A., Litvintseva L.V., Ulyanov I.S., Takahashi K., Ulyanov S.V., Yazenin A.V. and Hagiwara T. Soft computing optimizer for intelligent control systems design: the structure and applications. - Proc. CCCT 2003, Florida, 2003, Vol. VI, pp. 79-84. 7. Hagiwara T., Kaneko C., Diamante D. Smart intelligent control system based on soft and quantum computing: Part I. Optimization with new type of fitness function. - Proc. SCI 2003, Florida, 2003, Vol. III, pp. 410-416. 8. Panfilov S. A., Litvintseva L.V., Ulyanov I.S. and Takahashi K. Soft computing optimizer: structure and software for simulation of universal approximators. - Proc. ICSCCW 2003, Antalya, 2003, pp.112-122. 9. Litvintseva L.V., Takahashi K., Hagiwara T., Ulyanov I.S., Fujii Sh., Yazenin A.V. Robust smart control of essentially non-linear dynamic systems based on soft computing optimizer: stochastic and fuzzy simulation. - Proc. ICSCCW 2003, Antalya, 2003, pp. 91-103. 10. Ulyanov S.V., Panfilov S.A., Ulyanov I.S.., Takahashi K., Amato P., Branciforte M., Calabro A. and Porto D.M. Applied quantum computing for intelligent control: Structure and HW implementation of quantum gates. - Proc. CCCT 2003, Florida, 2003, Vol. I., pp. 158-163. 11. Panfilov S.A., Ulyanov I.S., Litvintseva L.V., Yazenin A.V. Fast algorithm for efficient simulation of quantum algorithm gates on classical computer. - Proc. SCI 2003, Vol. III, pp.416-421. 12. Ulyanov S.V., Takahashi K., Rizzotto G.G. and Kurawaki I. Quantum soft computing: global optimization and quantum learning processes - benchmarks of application in AI, informatics, and intelligent control systems. - Proc. SCI 2003, Vol. III, pp.422-428. 13. Ulyanov S.V., Takahashi K., Panfilov S.A., Ulyanov I.S., Amato P., Porto D.M. and Rizzotto G.G. Quantum soft computing via robust control: From structure and HW-implementation of quantum algorithm gates to classical efficient simulation of quantum soft computing and robust control. - Proc. ICSCCW 2003, Antalya, 2003, pp. 123-137. 14. US patent N 6,415,272 В1, 1998. System for intelligent control based on soft computing (Inventor: S.V. Ulyanov). |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=589&page=article |
Версия для печати Выпуск в формате PDF (1.54Мб) |
| Статья опубликована в выпуске журнала № 2 за 2004 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- Кросс-система автоматизации разработки программного обеспечения на базе языка высокого уровня Рада
- Параллельная обработка в алгоритмах визуализации с трассировкой лучей
- К вопросу параметризации свойств программных средств обучения
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
Назад, к списку статей



 являются открытыми системами, то есть позволяют вводить дополнительные критерии качества управления и ограничения на качественные характеристики процесса управления.
являются открытыми системами, то есть позволяют вводить дополнительные критерии качества управления и ограничения на качественные характеристики процесса управления. Основной проблемой при создании технологии проектирования робастных БЗ ИСУ является оптимизация процесса проектирования оптимальной БЗ для нечеткого контроллера (НК).
Основной проблемой при создании технологии проектирования робастных БЗ ИСУ является оптимизация процесса проектирования оптимальной БЗ для нечеткого контроллера (НК).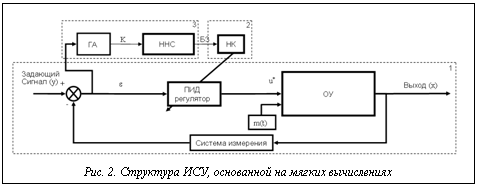 Ограниченные возможности по реализации сложных критериев качества управления в классических СУ, особенно в указанных выше случаях управления, послужили отправной точкой к развитию интеллектуальных СУ (ИСУ), основанных на идеях, близких к использованию стратегии управления, используемой человеком-экспертом в сложных ситуациях. Для моделирования человеко-машинных стратегий управления стали использоваться так называемые мягкие вычисления, в основе которых лежит теория нечетких подмножеств и нечеткий вывод [1,2]. Представленная на рисунке 2 структура последовательным наращиванием составляющих блоков классической СУ (блок 1) преобразуется в экспертную СУ введением блока нечеткого вывода 2 [3,4], и является первым поколением ИСУ.
Ограниченные возможности по реализации сложных критериев качества управления в классических СУ, особенно в указанных выше случаях управления, послужили отправной точкой к развитию интеллектуальных СУ (ИСУ), основанных на идеях, близких к использованию стратегии управления, используемой человеком-экспертом в сложных ситуациях. Для моделирования человеко-машинных стратегий управления стали использоваться так называемые мягкие вычисления, в основе которых лежит теория нечетких подмножеств и нечеткий вывод [1,2]. Представленная на рисунке 2 структура последовательным наращиванием составляющих блоков классической СУ (блок 1) преобразуется в экспертную СУ введением блока нечеткого вывода 2 [3,4], и является первым поколением ИСУ. (ti), òe(ti)dti} – вектор, компонентами которого являются ошибка управления, ее производная и интеграл ошибки соответственно, K(ti)={kp(ti), kd(ti), kl(ti)} – оптимальные (с точки зрения заданной функции пригодности ГА) параметры ПИД-регулятора; ti – момент времени.
(ti), òe(ti)dti} – вектор, компонентами которого являются ошибка управления, ее производная и интеграл ошибки соответственно, K(ti)={kp(ti), kd(ti), kl(ti)} – оптимальные (с точки зрения заданной функции пригодности ГА) параметры ПИД-регулятора; ti – момент времени.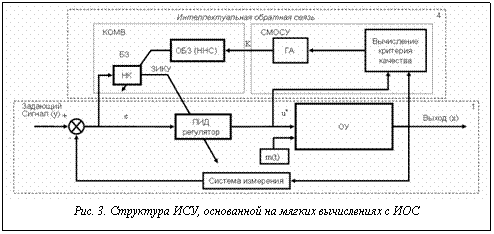 Задача эксперта при определении структуры ННС сводится к выбору модели нечеткого вывода и, главным образом, к лингвистическому описанию заданного ОС. Каждой из компонент ОС соответствует некоторая лингвистическая переменная, описывающая сигнал с помощью соответствующего этой лингвистической переменной терм-множества. Мощность терм-мно жества и параметры составляющих его элементов (класс и параметры функции принадлежности) неизвестны. "Полноту" лингвистического описания сигнала можно задать на уровне взаимосвязи терм-множеств, входящих в лингвистические переменные. Эту задачу в системах проектирования ИСУ, основанных на традиционных мягких вычислениях (второе поколение ИСУ), также решает человек-эксперт. Однако, как мы указывали выше, в сложных случаях управления эксперту трудно решить данную задачу вручную (то есть подобрать оптимальную структуру ННС для заданного ОС).
Задача эксперта при определении структуры ННС сводится к выбору модели нечеткого вывода и, главным образом, к лингвистическому описанию заданного ОС. Каждой из компонент ОС соответствует некоторая лингвистическая переменная, описывающая сигнал с помощью соответствующего этой лингвистической переменной терм-множества. Мощность терм-мно жества и параметры составляющих его элементов (класс и параметры функции принадлежности) неизвестны. "Полноту" лингвистического описания сигнала можно задать на уровне взаимосвязи терм-множеств, входящих в лингвистические переменные. Эту задачу в системах проектирования ИСУ, основанных на традиционных мягких вычислениях (второе поколение ИСУ), также решает человек-эксперт. Однако, как мы указывали выше, в сложных случаях управления эксперту трудно решить данную задачу вручную (то есть подобрать оптимальную структуру ННС для заданного ОС).
 ,
, , и
, и 
 , где tk – моменты времени, k=1,…,N, N равно числу точек в управляющем сигнале;
, где tk – моменты времени, k=1,…,N, N равно числу точек в управляющем сигнале;  – функции принадлежности входных переменных, l – индекс правила в БЗ; символ «П» обозначает операцию нечеткой конъюнкции (в частности, может интерпретироваться как произведение).
– функции принадлежности входных переменных, l – индекс правила в БЗ; символ «П» обозначает операцию нечеткой конъюнкции (в частности, может интерпретироваться как произведение). .
.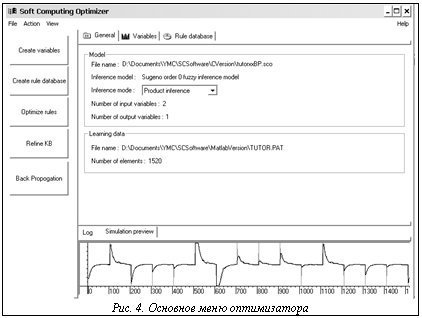 (‘Create rule base’), ГА2 для оптимизации следственной части нечетких правил (‘Optimize rules’), и ГА3, представляющий алгоритм перенастройки параметров лингвистических переменных для более точной аппроксимации обучающего сигнала полученными правилами (‘Refine KB’), а также алгоритм обратного распространения ошибки (‘Back propagation’), гарантирующий заданную точность аппроксимации обучающего сигнала
(‘Create rule base’), ГА2 для оптимизации следственной части нечетких правил (‘Optimize rules’), и ГА3, представляющий алгоритм перенастройки параметров лингвистических переменных для более точной аппроксимации обучающего сигнала полученными правилами (‘Refine KB’), а также алгоритм обратного распространения ошибки (‘Back propagation’), гарантирующий заданную точность аппроксимации обучающего сигнала 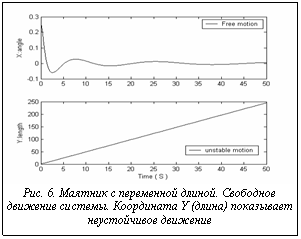 создавае- мой БЗ.
создавае- мой БЗ.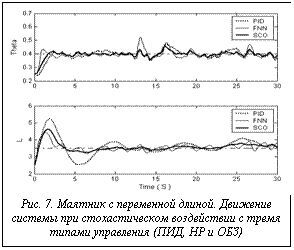 Функции принадлежности нечетких переменных редактора лингвистических переменных могут быть отредактированы вручную как перетаскиванием соответствующих значений, так и с помощью ручного ввода соответствующих параметров.
Функции принадлежности нечетких переменных редактора лингвистических переменных могут быть отредактированы вручную как перетаскиванием соответствующих значений, так и с помощью ручного ввода соответствующих параметров.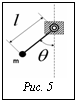 Нечеткие правила редактора базы нечетких правил структурно представлены в виде ННС. Число нейронов первого слоя соответствует числу входных сигналов. Число нейронов второго слоя соответствует суммарному числу функций принадлежности, входящих в лингвистические переменные, описывающие соответствующие входные сигналы. Число нейронов третьего слоя соответствует числу нечетких правил, задействованных в данной БЗ. Для выбора конкретного правила необходимо выбрать соответствующий нейрон третьего слоя. Выбранное правило можно изменить и дополнить.
Нечеткие правила редактора базы нечетких правил структурно представлены в виде ННС. Число нейронов первого слоя соответствует числу входных сигналов. Число нейронов второго слоя соответствует суммарному числу функций принадлежности, входящих в лингвистические переменные, описывающие соответствующие входные сигналы. Число нейронов третьего слоя соответствует числу нечетких правил, задействованных в данной БЗ. Для выбора конкретного правила необходимо выбрать соответствующий нейрон третьего слоя. Выбранное правило можно изменить и дополнить.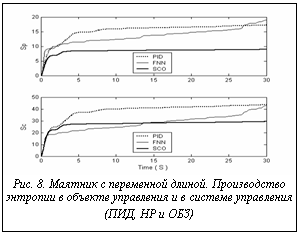 Маятник с переменной длиной
Маятник с переменной длиной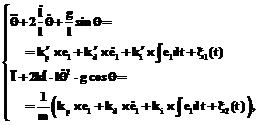 (1)
(1) . (2)
. (2)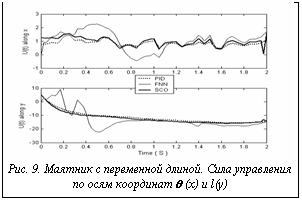
 Рассмотрим следующую задачу позиционного управления: при наличии рэлеевского стохастического шума, действующего на ОУ вдоль оси q (максимальная амплитуда шума равна 10), а также при наличии гауссовского стохастического шума вдоль оси l (максимальная амплитуда шума рав- на 4) удерживать движение объекта управления в заданном положении: qref = 0.4; lref = 3.5.
Рассмотрим следующую задачу позиционного управления: при наличии рэлеевского стохастического шума, действующего на ОУ вдоль оси q (максимальная амплитуда шума равна 10), а также при наличии гауссовского стохастического шума вдоль оси l (максимальная амплитуда шума рав- на 4) удерживать движение объекта управления в заданном положении: qref = 0.4; lref = 3.5.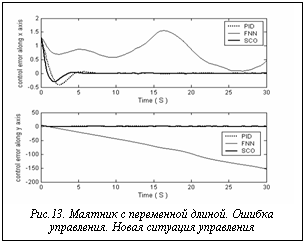 Рассмотрим задачу управления при следующих значениях параметров: m = 1, k = 1 и начальных условиях: [x0=2.5, y0=25], [
Рассмотрим задачу управления при следующих значениях параметров: m = 1, k = 1 и начальных условиях: [x0=2.5, y0=25], [ =0,
=0,  =0.01].
=0.01].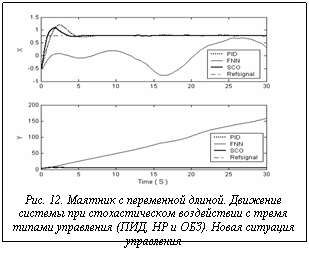 основе разработанного ОБЗ.
основе разработанного ОБЗ.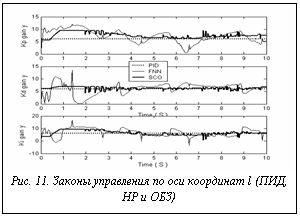 Полученные результаты моделирования позволяют сделать следующий вывод: с точки зрения критериев качества управления, таких как минимум ошибки управления, минимум производства энтропии в объекте управления и в системе управления (минимум тепловых потерь и потерь полезной работы и энергии) ИСУ, разработанная на основе ОБЗ, является более эффективной, чем ИСУ, разработанная с помощью традиционных мягких вычислений, а также эффективнее традиционных ПИД-регуляторов.
Полученные результаты моделирования позволяют сделать следующий вывод: с точки зрения критериев качества управления, таких как минимум ошибки управления, минимум производства энтропии в объекте управления и в системе управления (минимум тепловых потерь и потерь полезной работы и энергии) ИСУ, разработанная на основе ОБЗ, является более эффективной, чем ИСУ, разработанная с помощью традиционных мягких вычислений, а также эффективнее традиционных ПИД-регуляторов.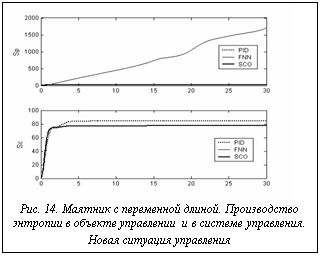 Рассмотрим задачу управления с новыми условиями, отличную от первоначальной задачи управления, для которой подбирался оптимальный ОС, и сравним результаты моделирования для трех указанных случаев управления.
Рассмотрим задачу управления с новыми условиями, отличную от первоначальной задачи управления, для которой подбирался оптимальный ОС, и сравним результаты моделирования для трех указанных случаев управления. = 0.78 (45°);
= 0.78 (45°);  = 5;
= 5;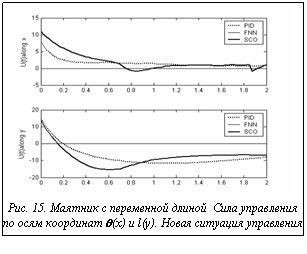 Примечания. На рисунках 12-17 управляющая сила и коэффициенты усиления для управления, основанного на традиционном методе мягких вычислений, равны нулю. Это означает, что полученная с помощью ННС БЗ НК неробастна, то есть для новых начальных данных в БЗ нет ни одного активируемого правила. Результаты моделирования показывают, что данная ИСУ не справляется с новой ситуацией управления.
Примечания. На рисунках 12-17 управляющая сила и коэффициенты усиления для управления, основанного на традиционном методе мягких вычислений, равны нулю. Это означает, что полученная с помощью ННС БЗ НК неробастна, то есть для новых начальных данных в БЗ нет ни одного активируемого правила. Результаты моделирования показывают, что данная ИСУ не справляется с новой ситуацией управления.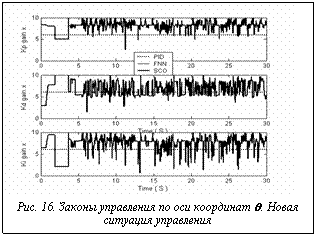 Перспективы развития программной системы
Перспективы развития программной системы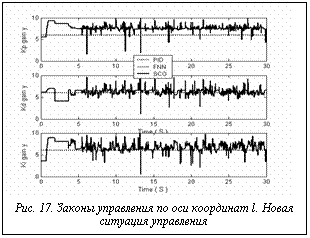 Разработанный ОБЗ может работать на одном пространстве решений (в силу предельных возможностей ГА). Для глобальной оптимизации на множестве пространств решений требуется разработать новый вид вычислений, позволяющий объединить множество пространств решений в одно множество решений [10-13]. Таким новым видом вычислений являются квантовые вычисления.
Разработанный ОБЗ может работать на одном пространстве решений (в силу предельных возможностей ГА). Для глобальной оптимизации на множестве пространств решений требуется разработать новый вид вычислений, позволяющий объединить множество пространств решений в одно множество решений [10-13]. Таким новым видом вычислений являются квантовые вычисления.