Принципы конструирования информационно-вероятностного метода осуществления долгосрочного прогноза
| Тихомиров В.А. (tva@npo-rit.ru) - Тверской государственный технический университет, доктор технических наук, Тихомиров ВЛ.А. () - , Макушкин А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Согласно современной концепции математики и ее отношению к реальности, основа построения информационно-вероятностного метода должна быть абстрагированной от реального происхождения. При обсуждении информационно-вероят ностного существа метода и его принципиальных особенностей значительное внимание уделено выявлению основополагающих идей, связанных с формулировкой метода на математическом языке. Формализацию задачи осуществим на основе концепции метода комитетов, рассматривая ее с позиции правомерного существования схемы нахождения сложного предпочтения на множестве альтернатив [1]. Комитетом оценки эффективности принимаемых стратегических решений назовем такое конечное множество векторов класса Решение сформулированной задачи связано, во-первых, с определением вектора Таблица 1 Морфологическая матрица
В качестве конструкции построения выборочного пространства воспользуемся образованием индуктивного предела Х банаховых подпространств Таблица 2 Модифицированная морфологическая матрица
При этом ситуацию возможной, но невыявленной неадекватности отображения оригиналу назовем ситуацией неопределенности. Поле таблицы представляет собой множество параметров, которые формируют в ситуации неопределенности некоторый оценочный потенциал сложной системы. Вес параметров в формировании оценочного потенциала характеризуется количественной мерой степени уверенности в ситуации объективно существующей неопределенности и отождествляется с распределением вероятностей
так и со сменой ингредиента на противоположный:
с отображением в Таблица 3 Матрица принятия стратегических решений
Элементы Данный подход позволил задачу выбора решения символически представить тройкой ({A}, {х}, p(a)), называемой вероятностным пространством принятия решений. При этом формализация осуществлена в рамках конструирования такого математического объекта, каким является абстрактная математическая модель принятия стратегического решения. Для выбора исходных математических объектов воспользуемся следующими положениями и рядом аксиом. Положение 1. В вероятностном смысле любые события сравнимы. Положение 2. Множество признаков должно с высокой эффективностью отображать оценочный потенциал. Положение 3. Имеет смысл существование априорного распределения вероятностей на множестве признаков Аксиома 1. Система оценок, отражающая степень уверенности в ситуации объективно существующей неопределенности, определяемая весом всех компонентов, формирующих оценочный потенциал, отождествляется с вероятностью р(а). Аксиома 2. Понятие интегрального потенциала элементарных событий отождествляется с вероятностью р(r). Аксиома 3. Для любого вероятностного пространства ({A},{х},p(a)) множество выбора {A} непусто, то есть всякая задача выбора решения может быть решена. Аксиома 4. Аксиомы теории вероятностей (Колмогорова). Поскольку с позиции теории информации всякий процесс развития представляется как процесс накопления информации, определяющей упорядоченность структуры развивающихся систем, вполне закономерной является оценка стратегического решения с помощью статистической формулы энтропии. Положение 4. Переход от содержательного уровня формирования цели прогноза к уровню, обеспечивающему экспликацию в виде показателей качества стратегического прогноза, осуществлен на основе применения средних энтропийных оценок. Информационные показатели раскрывают структуру системы; признаки, являющиеся входом в морфологическую матрицу, раскрывают функциональное предназначение данной структуры. Поэтому чем меньше взаимосвязь признаков, тем полнее они раскрывают функциональную сторону системы в целом. При этом если в конкретных условиях степень связи тех или иных признаков проявляется пренебрежительно слабо или не находит очевидного физического механизма, с помощью которого осуществлялась бы связь между ними, то это дает основание считать их физически независимыми. Аксиома 5. События, реальные прообразы которых причинно независимы, независимы в вероятностном смысле. Положения и аксиомы служат собственным основанием, необходимым для построения модели оценки перспективы развития систем различной физической природы. При этом разработанный подход к решению проблемы принятия стратегического решения отвечает условиям симметрии и строгого доминирования. Информация в вероятностно-статистической теории выступает в качестве снимаемой, уменьшаемой неопределенности, а ее количество измеряется посредством вероятности. Поэтому дальнейшее построение метода связано с исследованием законов преобразования информации поля декартова произведения двух множеств (альтернатив и признаков) в количественные составляющие информации. С этой целью в логическую схему введем такие понятия, как априорные, апостериорные и условные вероятности, применим теорему Байеса и формулу полной вероятности, а также введем понятие условной вероятности Для получения зависимости определения величины
Один из методов расчета вероятности проявления j-й характеристики сравниваемых вариантов на формирование оценочного потенциала основан на введенном В.В. Хоменюком понятии потенциального распределения вероятности, который определяется по формуле:
Принцип потенциального распределения вероятностей основан на том, что предпочитается выбор с большей вероятностью тех характеристик системы, свойства которой имеют большой вклад в суммарное значение оценочного потенциала. При этом отметим, что для принципа потенциального распределения вероятностей В.В. Хоменюка (4) априорная информация о состоянии характеристик основана на принципе недостаточности знаний. Однако не вызывает сомнения тот факт, что вес различных признаков в формировании оценочного потенциала различен. Получение оценок априорного распределения Стремление к широкому использованию априорной информации, задаваемой вероятностным образом, является самым примечательным в современной теории принятия решений. Ведь, вводя на основе оценок Фишборна априорную вероятность, мы, задавая "вход" в модель, учитываем различный вес характеристик в формировании оценочного потенциала. Затем, используя принцип потенциального распределения (4) и положения теоремы Байеса, получаем логически обоснованный "выход" из модели в виде апостериорных условных вероятностей в форме:
Таким образом, польза от введения априорной вероятности, с одной стороны, состоит в том, что это дает присоединение необходимой для анализа информации, а с другой стороны, это выигрыш с точки зрения логической ясности. /p> После введения априорной вероятности в модель принятия решения и вычисления апостериорного значения условной вероятности
Однако целью анализа эффективности принимаемого решения является в некотором смысле не оценка информации о параметрах, которую можно извлечь из входных данных, а выбор одного из альтернативных способов действия и изучения процесса принятия решений. Будем исходить из того, что процесс принятия гипотезы H0 подвергается четкому логическому анализу с позиции математической статистики. Для построения решающего алгоритма воспользуемся аналогией статистических понятий, а именно понятиями ошибок первого и второго рода. Так, ошибка первого рода заключается в непринятии проверяемой гипотезы H0, когда она верна. Вероятность совершения такой ошибки Измерение степени упорядоченности и степени организации системы осуществляется через количество энтропии. Тогда уровень значимости оценим через функцию неопределенности:
При этом в принятой системе договоренностей не опровергается та гипотеза, которой соответствует меньшее значение величины:
где Известно, что количество накопленной и сохраняемой в структуре систем информации
Чтобы любая система в процессе своей эволюции не достигла предела "приспособленности" (в результате которого системы существуют только в определенных жестко детерминированных условиях), она должна сохранять в себе непредсказуемость, характеризуемую определенной порцией энтропии. Удельный вес этой порции определяется зависимостью: На примере вариантов научного поиска дадим содержательную интерпретацию данной зависимости. Если бы научный поиск оптимального варианта системы любой физической природы был чисто случайным, это означало бы равенство вероятностей всех направлений поиска. Такой ситуации соответствует полное отсутствие предварительной информации Ii=0, то есть Достаточное количество фактов (в социологии, исследовании текстов, биологии, химии, физике, кибернетике в [2-5]) свидетельствует в пользу выдвижения гипотезы о существовании оптимального значения величины GH, характеризующей удельный вес порции энтропии. С целью получения подтверждения данной гипотезы был проведен анализ некоторых положений естественных наук, который показал следующее. Общее у всех естественных наук в том, что в качестве существенного они выделяют все же определенное содержание отображаемой действительности, то есть некоторые конкретные ее свойства или отношения. Различие между этими науками состоит в специфике содержания, которая определяется, в свою очередь, спецификой задач, решаемых данной наукой и ее практическими приложениями. Поэтому чтобы применить индуктивный переход от частных фактов конкретной области науки к другим, с более высоким уровнем общности, реализуем основные положения аксиоматического метода. Структура метода формируется следующими основными требованиями [3, 6]: 1) выбираем исследуемый объект; 2) воспользуемся общими положениями математической теории, отражающими количественные отношения действительности, которые являются формой в чистом виде, то есть то общее, что имеют все изоморфные с этой системой системы объектов; 3) формируем схему дедуктивного вывода, то есть осуществляем объяснение, переходя от законов одной максимальной степени общности к другим (конкретным), обеспечивая тем самым переход к выводимому факту (в наших исследованиях – это нахождение оптимального значения удельного веса энтропии GH ). Исходной посылкой к выбору объекта исследования послужил закона Бенфорда и то, что большинство явлений в природе носит экспоненциальный характер. Бенфорд провел исследования на основе анализа более 20 тысяч чисел, представленных в различных таблицах, и установил эмпирический "закон аномальных чисел" – вероят- ность р, которая определяется по формуле: pi = log(1+1/i) , где i =1,2,3,...,9; и означает то, что у некого случайного числа первая значащая цифра будет равна i. Данный тип зависимости относится к экспоненциальному классу, функции которого отождествляются с мерой неопределенности первого рода. Следующий шаг конструктивистского метода связан с решением задачи минимизации меры неопределенности. Решение данной задачи обеспечит определение количественного значения удельного веса энтропии. С учетом класса функции неопределенности обобщенная мера неопределенности H(x), xÎ[0,1] определяется равенством:
Класс функций H{x} поставляет различные меры неопределенности в зависимости от выбора конкретного вида функций f(x) и φ(х). Наибольшую прагматическую ценность имеет экспоненциальная функция вида: f(x) = xeax+β,
Положив φ(k) = ln k, (7) получаем функцию неопределенности, которая рассматривалась в качестве основного типа. Исходя из того, что любая экспоненциальная функция есть частный случай показательной функции y=f(x) = baсх, в качестве исходного объекта исследования была взята задача о выборе оптимальной системы счисления. Физическая интерпретация данной задачи связана с тем, что, оценивая пригодность той или иной системы счисления в качестве основы для конструирования вычислительной машины (кроме простоты осуществления арифметических операций в ней), имеет значение также и экономичность системы. Под этим понятием в данном случае имеется в виду тот запас чисел, которые можно записать в данной системе с помощью определенного количества знаков. Формализация задачи проводилась по следующей схеме. В общем случае, если взять n знаков, а за основание системы счисления принять некоторое число х, то получится x/n разрядов, и количество чисел, которые при этом можно записать, будет равно xn/x (то есть это вид функции y=f(x) = baсх при условии, что c=0, а b= xn/x). Общим принципом, обеспечивающим решение задачи в форме y=xn/x, является принцип максимума энтропии, предписывающий суждениям необходимость отражения всей доступной информации. В качестве основного условия решения задачи о выборе оптимальной системы счисления выбрано условие экстремальности. С этой целью рассмотрим выражение xn/x как функцию переменной х, принимающей не только целые, но и любые (дробные, иррациональные) положительные значения. Тогда поиск значения переменной х, при котором эта функция достигает максимума, связан с необходимым условием, что в точке x0 функция у(х0) достигает максимума. Условие выполняется, если обращается в нуль производная функции в этой точке. Производная равна:
приравняв ее к нулю, получим, что ln x = 1, то есть х=е. Число е приближенно равно 2,7182..., ближайшее к е целое число есть 3 – оно и служит основанием наиболее экономичной системы счисления. В ходе решения данной задачи принцип максимума энтропии был выполнен. При этом развитие рассмотренной выше схемы рассуждений, связанное с определением оптимального значения величины GH, осуществлялось с учетом следующих положений. Так, для того чтобы не нарушить общность подхода, класс функций f(GH) должен удовлетворять определенным условиям: 1) функция f(GH) – непрерывная, ограничена в интервале [0,1] и имеет производную во всех внутренних точках этого интервала; 2) функция f(GH)/ GH монотонно убывает на интервале [0,1]; 3) функция f(GH) неотрицательная при всех GH Î [0,1]. Причем операция, обеспечивающая выполнение условия GHопт Î [0, 1], осуществима на основе применения зависимости (1), исходя из того, что xmin = Gmin,H = 0 (xmin = 0, нуль при этом интерпретируется как выбор любой системы счисления). Однако возникает проблема исключения произвола в выборе Gmax,H, то есть при переходе от одной общности рассуждений к другой в выборе максимально возможного значения основания системы счисления xmax. Исключение произвола и организация такого индуктивного перехода осуществлялась на основе принципа минимума энтропии (суждения не должны быть отражением большего объема информации, чем тот, которым располагают, то есть имеем дело только с цифрами). Физическая интерпретация данного принципа в контексте рассматриваемой задачи связана с определением минимального числа разрядов для представления определенной цифры в той или иной системе счисления. При этом исходим из условия, что все цифры равноправны в выбранной системе счисления, то есть если сделан выбор конкретной системы счисления, то при минимальной разрядности должна существовать возможность представления любой из цифр выбранной системы. Исходя из того, что единичный разряд является минимальным для представления числа (хотя бы одного) в любой системе счисления, однако максимально возможной системой (при заданных ограничениях – условиях и без привлечения дополнительных договоренностей, то есть соблю- дение принципа минимума) является десятичная, то есть xmax = Gmax,H = 10. Данный подход и принцип относительности определения (его применение связано с тем, что специфический признак выбирается не произвольно, а относительно требований, вытекающих из сущности условия минимизации энтропии) обеспечили получение величины GHопт = 0,2718. Таким образом, разработанный конструктивистский метод обеспечил возможность перехода от одной формы общности к другой и дал возможность выражать различное содержание через форму, обеспечивая диалектическое «снятие» неопределенности содержания. При этом на основе разработанного конструктивистского метода был осуществлен индуктивный переход и получено оптимальное значение величины GHопт = 0.2718, а интервал 0.25£ GHопт £ 0.3 – это интервал наилучшего соотношения непредсказуемости и детерминированности. Следовательно, чем больше расчетная величина GiH отличается от оптимального значения, тем выше вероятность принятия гипотезы Величины На этом процесс построения абстрактной математической модели, оценки эффективности систем различной физической природы окончен. При этом информационно-вероятностный метод позволяет осуществить переход к формализованному уровню описания процесса становления, уменьшает энтропию конкуренции вариантов, исключает тупиковые пути отбора различных систем, обеспечивает определение круга наиболее актуальных вариантов в долгосрочной перспективе. Список литературы 1. Мартыщенко Л.А., Тихомиров В.А. Вероятностно-статистические методы праксеологического анализа разработок и оценки технических решений -Л.: МО РФ, 1992. - 162 с. 2. Крылов Н.С. Работы по обоснованию статистической физики. – Изд-во АН СССР, 1950. 3. Эбилинг В., Энгель А., Файстель Р. Физика процессов эволюции. - М.: Эдиториал УРСС, 2001. 4. Пригожин И., Стенгерс И. Время, хаос, квант. К решению парадокса времени. – М.: Эдиториал УРСС, 2001. 5. Седов Е.А. Одна формула и весь мир -М: Знание,1982. 6. Седов Е.А. Эволюция и информация. – М.: Наука, 1976. 7. Спиркин А.Г. Философия. – М.: Гардарика, 1998. 8. Тихомиров В.А. Построение абстрактной математической модели оценки качества технических систем.//Сб. докл. Междунар. науч.-технич. конф. – Пенза: ПГУ, 1998 – С. 66 – 69. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
http://swsys.ru/index.php?id=590&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
- Метод интегрированного описания топологических отношений в геоинформационных системах
- Кросс-система автоматизации разработки программного обеспечения на базе языка высокого уровня Рада
- Интегрированная система «микросреда»
- Информационная поддежка технического обеспечения кораблей при первой операции флота

 для которого принятие нулевой гипотезы
для которого принятие нулевой гипотезы  при заданном уровне значимости обеспечивает определенное число компонентов вектора
при заданном уровне значимости обеспечивает определенное число компонентов вектора  .
. и мощности критерия
и мощности критерия  стратегического прогноза. Информационное отображение конкретной ситуации при этом укладывается в следующую схему: имеется n сравниваемых между собой альтернатив; каждой альтернативе поставлена в соответствие совокупность m характеристик, определяющих потенциальные возможности системы. В этом случае ситуация принятия решений в развернутой форме характеризуется таблицей состояний (табл. 1), у которой один вход образован множеством альтернатив
стратегического прогноза. Информационное отображение конкретной ситуации при этом укладывается в следующую схему: имеется n сравниваемых между собой альтернатив; каждой альтернативе поставлена в соответствие совокупность m характеристик, определяющих потенциальные возможности системы. В этом случае ситуация принятия решений в развернутой форме характеризуется таблицей состояний (табл. 1), у которой один вход образован множеством альтернатив  , а другой – множеством признаков {
, а другой – множеством признаков { }. При этом характеристики образуют выборочное пространство, а альтернативы – систему подмножеств выбо- рочного пространства, элементам которого соответствуют свойства, имеющие практическую ценность.
}. При этом характеристики образуют выборочное пространство, а альтернативы – систему подмножеств выбо- рочного пространства, элементам которого соответствуют свойства, имеющие практическую ценность.














 . Данный прием обеспечил возможность представления поля исходной таблицы 1 в виде таблицы 2, образованной в результате декартова произведения
. Данный прием обеспечил возможность представления поля исходной таблицы 1 в виде таблицы 2, образованной в результате декартова произведения  множеств альтернатив и признаков, формирующих образ (отображение) реальных ситуаций.
множеств альтернатив и признаков, формирующих образ (отображение) реальных ситуаций.


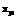

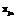



 . Компоненты {xji} однозначно задаются в различных физических шкалах. Поэтому для приведения компонентов {xji} к единой общей шкале воспользуемся естественной нормализацией, осуществляемой относительно экстремальных значений компонентов {
. Компоненты {xji} однозначно задаются в различных физических шкалах. Поэтому для приведения компонентов {xji} к единой общей шкале воспользуемся естественной нормализацией, осуществляемой относительно экстремальных значений компонентов { } как без смены ингредиента на противоположный:
} как без смены ингредиента на противоположный: , (1)
, (1) , (2)
, (2) . Зависимости (1) и (2) обеспечили отображение выборочного пространства (табл. 2) в другое, имеющее мощность континуума (табл. 3).
. Зависимости (1) и (2) обеспечили отображение выборочного пространства (табл. 2) в другое, имеющее мощность континуума (табл. 3).
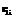







 (пространства мощности континуума) в единой шкале будем идентифицировать с элементарными событиями. При этом определенная на
(пространства мощности континуума) в единой шкале будем идентифицировать с элементарными событиями. При этом определенная на  нормированная мера соответствует вероятности
нормированная мера соответствует вероятности  , которая отождествляется с понятием интегрального потенциала заданного комплекса элементарных событий. Смысл данной меры состоит в том, чтобы соответствующим образом интерпретировать понятие вероятность. При этом вероятность как категория диалектики совмещает в себе и меру объективной возможности события и степень субъективной уверенности в появлении событий. С целью формализации задачи выбора решения множество альтернатив идентифицируем с пространством событий {A}, а множество признаков с событиями {х}. Тогда связь между всеми компонентами, формирующими оценочный потенциал системы, осуществляется через определенную на этих компонентах нормированную меру, которая отождествляется с вероятностью p(a). Распределение вероятностей p(a) обеспечивает оценку нулевой гипотезы
, которая отождествляется с понятием интегрального потенциала заданного комплекса элементарных событий. Смысл данной меры состоит в том, чтобы соответствующим образом интерпретировать понятие вероятность. При этом вероятность как категория диалектики совмещает в себе и меру объективной возможности события и степень субъективной уверенности в появлении событий. С целью формализации задачи выбора решения множество альтернатив идентифицируем с пространством событий {A}, а множество признаков с событиями {х}. Тогда связь между всеми компонентами, формирующими оценочный потенциал системы, осуществляется через определенную на этих компонентах нормированную меру, которая отождествляется с вероятностью p(a). Распределение вероятностей p(a) обеспечивает оценку нулевой гипотезы  при заданном уровне значимости
при заданном уровне значимости  и мощности критерия
и мощности критерия  стратегического прогноза.
стратегического прогноза. проявления j-й характеристики в формировании оце- ночного потенциала при условии, что собы- тия, формирующие оценочный потенциал, произошли.
проявления j-й характеристики в формировании оце- ночного потенциала при условии, что собы- тия, формирующие оценочный потенциал, произошли. (3)
(3) (4)
(4) связано с отношением порядка, которое подробно исследовано в трудах Фишборна. Для простого линейного отношения порядка оценки Фишборна априорных вероятностей образуют убывающую арифметическую прогрессию вида:
связано с отношением порядка, которое подробно исследовано в трудах Фишборна. Для простого линейного отношения порядка оценки Фишборна априорных вероятностей образуют убывающую арифметическую прогрессию вида: 
 (5)
(5) и
и 
 называется уровнем значимости. Уровень значимости
называется уровнем значимости. Уровень значимости 
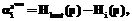
 – значение энтропии гипотетического варианта, обладающего оптимальными характеристиками для данной информационной ситуации;
– значение энтропии гипотетического варианта, обладающего оптимальными характеристиками для данной информационной ситуации;  – значение энтропии для i-го варианта системы.
– значение энтропии для i-го варианта системы. в точности равно уменьшению их энтропии
в точности равно уменьшению их энтропии  . При этом разность между энтропией
. При этом разность между энтропией  в рассмотренной информационной ситуации и есть количество информации
в рассмотренной информационной ситуации и есть количество информации 
 .
. . Тогда как при GH=0 невозможно было бы создание новой системы. Данное положение свидетельствует о том, что между заранее запланированными направлениями научно-технического поиска и теми новыми исследованиями, которые возникают в ходе реализации этого плана, должно существовать оптимальное отношение.
. Тогда как при GH=0 невозможно было бы создание новой системы. Данное положение свидетельствует о том, что между заранее запланированными направлениями научно-технического поиска и теми новыми исследованиями, которые возникают в ходе реализации этого плана, должно существовать оптимальное отношение. . (6)
. (6) , которая будет функцией неопределенности, если предположить, что вещественный коэффициент а ≤ 0. Тогда f(x)
, которая будет функцией неопределенности, если предположить, что вещественный коэффициент а ≤ 0. Тогда f(x)  и обобщенная мера неопределенности
и обобщенная мера неопределенности

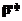 количественно характеризуют систему договоренностей, необходимую для осуществления стратегического прогноза.
количественно характеризуют систему договоренностей, необходимую для осуществления стратегического прогноза.