Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Построение маршрута с максимальной пропускной способностью методом последовательного улучшения оценок
Аннотация:
Abstract:
| Автор: Котов А.С. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 20161 |
Версия для печати Выпуск в формате PDF (1.54Мб) |
В ряде работах [1,2] построение маршрута с максимальной пропускной способностью производится непосредственно на сети, представленной графом. Такие методы, обладая хорошей наглядностью (особенно если сеть достаточно проста), затрудняют использование ЭВМ как для хранения исходной информации, так и для процесса оптимизации. Метод улучшения оценок рассчитан на представление сети (графа) в виде матрицы смежности c Следуя [1], некоторый произвольный маршрут (путь)
где указаны номера вершин, или дуги. Множеству дуг (i,j), принадлежащих маршруту mk,l (1), соответствует множество их пропускных способностей {cij}. Минимальная из этих пропускных способностей определяет собой критическую пропускную способность всего пути pk,l:
где (ik,jl) – критическая дуга маршрута mk,l. Например, для некоторого произвольного маршрута m1,6, построенного по матрице пропускных способностей (табл. 1) m1,6=á1,4,5,3,6ñ, пропускная способность и критическая дуга, согласно (2), равны (критическая дуга в маршруте m1,6 выделена жирным шрифтом): p1,6= =min{5,7,2,3}= c5,3= 2 Þ(i1,j6) =(5;3) Однако от вершины Al к вершине A6 существует целое множество
Таблица 1 c = || cij ||, j=1 j,l
Из всех Nn возможных маршрутов построение оптимального пути от пункта Ak к Al можно записать как решение следующей оптимизационной задачи на графе:
при условиях:
Примечание. Количество возможных путей Nn от вершины Ak до вершины Al при произвольной матрице c (j<1 – коэффициент полноты – доля значащих (cij>0) элементов матрицы) можно оценивать сверху (при j=1, табл. 1) по рекуррентной формуле:
где r – количество промежуточных элементов, расположенных в маршруте mk,l между концевыми элементами k и l. Например, для n=6 имеем N6=65, при этом Nn быстро увеличивается по мере увеличения размера n матрицы c (N10=104001). Довольно простая формальная запись задачи о пропускной способности маршрута в комбинаторной ее постановке возможна благодаря сложности самих переменных mk,l по сравнению со скалярными переменными, с которыми, как правило, приходится иметь дело при постановке задачи в форме задачи математического программирова- ния [3]. Обычно существенно отличаются от классических и методы решения комбинаторных задач, нося специальный, порой и явно неформальный характер. Таблица 1 c = || cij ||. j=1 j,l
Таблица 2 Совмещенная матрица
Рассматриваемый ниже метод последовательного улучшения оценок, в частности, также носит неформальный характер. Суть метода последовательного улучшения оценок для построения оптимального маршрута
где первый и второй элементы в (7) означают максимально возможную пропускную способность соответственно начальной и конечной дуг оптимального маршрута Более подробно некоторые детали метода улучшения оценок, а также возможность определения всего множества оптимальных маршрутов рассмотрим на следующих двух числовых примерах. Пример 1. Найти оптимальный маршрут от пункта A6 к пункту A2 и его пропускную способность Начальная оценка (t=1) максимальной пропускной способности, согласно (7), равна (табл. 1):
Из пункта A6 начинается построение множества маршрутов t=1,
где It – множество номеров вершин (строк), вошедших в маршрут Из таблицы 1 видно, что при данной оценке переход из пункта A6 возможен только в A3. Поскольку из вершины A3 возможен переход только в A6 ( Так как номер концевой вершины j1=3 не равен требуемому (l=2), то необходимо перейти к улучшенной оценке Для определения улучшенной оценки
Номер
где коэффициенты cij в i-й строке выбираются только из тех столбцов j, номера которых еще не вошли в маршруты { Для рассматриваемого примера, согласно (10) и таблице 1, имеем: I=k=6:
i=3: min{26-23; 26-18; 26-14; 26-24}= 26-24=2 Þ c3,5=24, В соответствии с (9) и (11) улучшенная оценка максимальной пропускной способности от пункта A6 к A3 равна:
От пункта A6 начинается построение множества оптимальных маршрутов с использованием дуг, для которых пропускная способность не ниже полученной оценки. На основании таблицы 1 имеем: t=2, где под стрелками записаны пропускные способности соответствующих дуг. Поскольку концевой элемент j2=2 совпал с концевым элементом искомого маршрута (l=2), то решение получено, при этом множество оптимальных маршрутов составил только один маршрут (12). Его пропускная способность максимальна и равна текущей оценке Таблица 2 Совмещенная матрица
Пример 2. По данным таблицы 1 найти маршрут Согласно (7) и таблице 1, начальная оценка равна:
По оценке t=1,
Из пункта A2 не существует дуг с пропускной способностью не меньшей, чем В строках
Новая оценка приводит к множеству оптимальных решений:
t=2,
Полученные решения заносятся в таблицу 2. Рассмотренные примеры и их анализ позволяют сформулировать алгоритм построения маршрутов с максимальной пропускной способностью (см. блок-схему алгоритма). Поскольку алгоритм решения достаточно прост, то ограничимся только некоторыми определенными замечаниями, которые могут оказаться полезными при разработке программы. В частности, при построении маршрутов Второе замечание касается пунктов 50 и 60, которые обеспечивают наиболее рациональный выбор каждой очередной улучшенной оценки Если в примере 2 вместо выбора оценки согласно пунктам 50 и 60 применить более простой способ выбора – по убыванию значений элементов cij в матрице c – то, начиная с
(то есть Из (13) видно, что при простом способе выбора оценки
Используя сформулированное условие оптимальности, убедимся, что полученное множество решений (13) оптимально. Для этого достаточно в матрице c ближайший по значению к
С оценкой В заключение отметим, что метод не потребует изменений в случае неполной матрицы c (j<1). Список литературы 1.Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. - М.: МЦНМО, 2002. – 960 с. 2.Берж К. Теория графов и ее применения: М.: Изд-во ин. лит-ры, 1962. – 320 с. 3.Карманов В.Г. Математическое программирование. – М.: Наука, 1986. – 285 с | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?id=595&like=1&page=article |
Версия для печати Выпуск в формате PDF (1.54Мб) |
| Статья опубликована в выпуске журнала № 2 за 2004 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
- Оптимизация обработки информационных запросов в СУБД
- Методы восстановления пропусков в массивах данных
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- Автоматизированная информационная система маркетолога
Назад, к списку статей



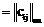 , где cij – пропускная способность участка сети от вершины Ai до вершины Aj, то есть дуги (i,j). Матрица
, где cij – пропускная способность участка сети от вершины Ai до вершины Aj, то есть дуги (i,j). Матрица  c может быть и несимметричной ($cij¹cji), что не повлияет на предлагаемый метод построения оптимального маршрута
c может быть и несимметричной ($cij¹cji), что не повлияет на предлагаемый метод построения оптимального маршрута  от вершины (пункта) Ak к вершине Al, то есть маршрута, обладающего наибольшей пропускной способностью –
от вершины (пункта) Ak к вершине Al, то есть маршрута, обладающего наибольшей пропускной способностью – 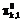 .
. от Ak к Al будем обозначать как упорядоченную последовательность вершин, соединенных дугами:
от Ak к Al будем обозначать как упорядоченную последовательность вершин, соединенных дугами: , (1)
, (1) , (2)
, (2) {c1,4, c4,5, c5,3, c3,6}=
{c1,4, c4,5, c5,3, c3,6}= возможных путей, среди которых содержится, по крайней мере, один оптимальный (то есть имеющий наибольшую пропускную способность
возможных путей, среди которых содержится, по крайней мере, один оптимальный (то есть имеющий наибольшую пропускную способность  ). В частности, между указанными пунктами оптимальными являются следующие два маршрута:
). В частности, между указанными пунктами оптимальными являются следующие два маршрута: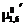 =á1,5,2,4,6ñ,
=á1,5,2,4,6ñ, =min{22,28,23,25}=22,
=min{22,28,23,25}=22, ,
, ={22,28,22,29}=22.
={22,28,22,29}=22. , (3)
, (3) , (4)
, (4) . (5)
. (5)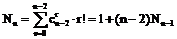 ,
,  , (6)
, (6)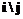
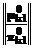 .
.







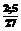


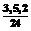



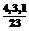














 ) состоит в том, что, начиная с некоторой исходной оценки сверху
) состоит в том, что, начиная с некоторой исходной оценки сверху  искомой максимальной пропускной способности
искомой максимальной пропускной способности  соответствует некоторое множество Gt={ci,j}t элементов матрицы c, не меньших значения оценки
соответствует некоторое множество Gt={ci,j}t элементов матрицы c, не меньших значения оценки  . Любой маршрут
. Любой маршрут  , построенный на этом множестве, будет иметь пропускную способность не меньшую, чем оценка
, построенный на этом множестве, будет иметь пропускную способность не меньшую, чем оценка  равна текущей оценке
равна текущей оценке  {
{ }, (7)
}, (7) , при этом естественно, что его пропускная способность
, при этом естественно, что его пропускная способность  ,
,  .
. по дугам с пропускными способностями не ниже оценки
по дугам с пропускными способностями не ниже оценки  –
–  :
: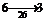 <,
<, 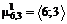 ,
,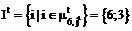 , (8)
, (8) на t-й итерации при оценке
на t-й итерации при оценке  ), то это приведет к образованию цикла, поэтому процесс построения маршрута прекращается.
), то это приведет к образованию цикла, поэтому процесс построения маршрута прекращается. . Это позволит начать построение нового множества маршрутов. Такое множество образуется при разветвлении маршрута в любой из его вершин, если в соответствующей строке матрицы c окажется более одного элемента cij не меньшего значения новой оценки
. Это позволит начать построение нового множества маршрутов. Такое множество образуется при разветвлении маршрута в любой из его вершин, если в соответствующей строке матрицы c окажется более одного элемента cij не меньшего значения новой оценки  . Ветвление маршрута позволит выявить все множество оптимальных маршрутов, если оно существует.
. Ветвление маршрута позволит выявить все множество оптимальных маршрутов, если оно существует. и из этих элементов наибольший взять в качестве новой оценки:
и из этих элементов наибольший взять в качестве новой оценки: . (9)
. (9) наибольшего элемента
наибольшего элемента  в i-й строке на t-й итерации найдется из условия:
в i-й строке на t-й итерации найдется из условия: (10)
(10) =
= , (11)
, (11) =5.
=5. .
. :
: 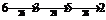 <
< ,
,  , (12)
, (12) . Оптимальный маршрут записан в совмещенной матрице – (таблица табл. 2).
. Оптимальный маршрут записан в совмещенной матрице – (таблица табл. 2). и
и  .
. .
.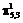 строится множество маршрутов:
строится множество маршрутов: :
:  <,
<,  ,
, .
. . Процесс закончен, но решение не получено – требуется улучшить оценку.
. Процесс закончен, но решение не получено – требуется улучшить оценку. ближайшими к оценке
ближайшими к оценке  и c2,4=23 (см. (10)). Следовательно, согласно (9), улучшенная оценка равна:
и c2,4=23 (см. (10)). Следовательно, согласно (9), улучшенная оценка равна: .
.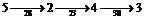 <,
<, = á5,2,4,3ñ
= á5,2,4,3ñ :
:  . (13)
. (13) <,
<, = á5,2,4,6,3ñ.
= á5,2,4,6,3ñ. (пункт 30) следует иметь в виду, что в любом из них не могут содержаться две одинаковые вершины, так как это означало бы наличие цикла. Удаление из маршрута цикла не может ухудшить решение. Действительно, если цикл содержит в себе критическую дугу, то ее удаление вместе с циклом способно только улучшить решение. Если такая дуга не входит в цикл, то на пропускную способность маршрута удаление цикла влияние не окажет. В алгоритме предусмотрены меры, исключающие возможность возникновения циклов. Из сказанного следует, что оптимальный маршрут не может содержать более чем n элементов (n-1 дуг).
(пункт 30) следует иметь в виду, что в любом из них не могут содержаться две одинаковые вершины, так как это означало бы наличие цикла. Удаление из маршрута цикла не может ухудшить решение. Действительно, если цикл содержит в себе критическую дугу, то ее удаление вместе с циклом способно только улучшить решение. Если такая дуга не входит в цикл, то на пропускную способность маршрута удаление цикла влияние не окажет. В алгоритме предусмотрены меры, исключающие возможность возникновения циклов. Из сказанного следует, что оптимальный маршрут не может содержать более чем n элементов (n-1 дуг). , что ведет к уменьшению объема вычислений при решении. Это видно из следующего сравнения.
, что ведет к уменьшению объема вычислений при решении. Это видно из следующего сравнения.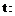 1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6 28, 27, 26, 25, 24, 23 (14)
28, 27, 26, 25, 24, 23 (14) ).
). потребуется выполнить 5 итераций, в то время как при способе, реализованном в алгоритме (пункты 50 и 60), потребовалась только одна итерация (соответствующие оценки в (14) выделены жирным шрифтом). Для задач больших размеров (n>1000) это может существенно снизить объем вычислений.
потребуется выполнить 5 итераций, в то время как при способе, реализованном в алгоритме (пункты 50 и 60), потребовалась только одна итерация (соответствующие оценки в (14) выделены жирным шрифтом). Для задач больших размеров (n>1000) это может существенно снизить объем вычислений.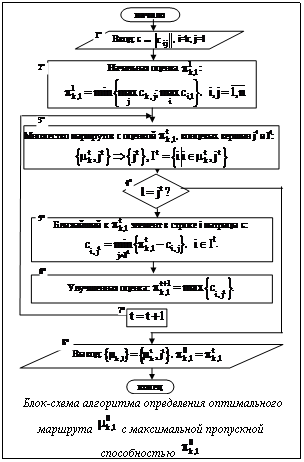 Заметим, что для любого произвольно выбранного маршрута можно определить, является ли он оптимальным или его пропускную способность можно увеличить. Для этого используется следующее достаточное условие оптимальности: если маршрут mk,l оптимален, то не существует другого маршрута m¢k,l, имеющего более высокую оценку, чем маршрут mk,l.
Заметим, что для любого произвольно выбранного маршрута можно определить, является ли он оптимальным или его пропускную способность можно увеличить. Для этого используется следующее достаточное условие оптимальности: если маршрут mk,l оптимален, то не существует другого маршрута m¢k,l, имеющего более высокую оценку, чем маршрут mk,l. . Такой оценкой является элемент
. Такой оценкой является элемент  . В таблице 1 выделяются все элементы cij не меньшие, чем
. В таблице 1 выделяются все элементы cij не меньшие, чем  (в таблице 1 эти элементы выделены жирным шрифтом). Остается убедиться, что не существует ни одного маршрута m5,3 на множестве выделенных элементов. На основании таблицы 1 имеем:
(в таблице 1 эти элементы выделены жирным шрифтом). Остается убедиться, что не существует ни одного маршрута m5,3 на множестве выделенных элементов. На основании таблицы 1 имеем: :
: 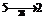 <
<  .
.