Об оптимальной раскладке символов на клавиатуре
| Усманов З.Д. (zafar-usmanov@rambler.ru) - Российско-Таджикский (Славянский) университет (профессор), Душанбе, Таджикистан, доктор физико-математических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
В 1867 г. К. Шоулс и С. Суле представили свое изобретение – первую в мире печатающую машинку. Можно предположить, что в ту пору авторов заботило прежде всего продвижение собственного, принципиально нового механического устройства и в меньшей степени то, каким образом следует располагать буквы на его клавиатуре. Раскладка, примененная ими, оказалась достаточно бесхитростной: на клавишах, сконструированных в два ряда, латинские буквы размещались в алфавитном порядке. Дефекты такого решения проявлялись в случаях скоростного печатания. При последовательном нажатии соседних клавишей соответствующие им исполнительные механизмы – молоточки с закрепленными на них литерами – нередко зацелялись друг за друга, застопоривая дальнейшую работу пишущей машинки. В последующем К. Шоулс, пытаясь устранить этот недостаток, предложил другую раскладку, в которой буквы, наиболее часто встречающиеся в английских текстах парами, разместились в разных местах клавиатуры. Такая раскладка получила название по шести первым буквам верхнего ряда клавиатуры – QWERTY. Таким образом, необходимость решения проблемы раскладки впервые была инициирована конструктивными особенностями печатного механизма. Однако у этой проблемы выявилась и другая, не менее важная сторона. Дело в том, что от характера раскладки букв на клавиатуре зависит скорость набора. Поэтому вполне естественно было ожидать появление исследований именно в этом направлении, что и было осуществлено в 1930-х годах профессором Двораком. Детально изучив технику печатания, он предложил новую раскладку, в которой с учетом частот встречаемости латинских букв наиболее частые из них разместились в среднем ряду, менее частые – в верхнем и редкие – в нижнем рядах. Кроме того, все гласные буквы расположились в левой части клавиатуры. По утверждению А. Дворака, его раскладка в сравнении с QWERTY позволила увеличить скорость печатания на 70 %. Результаты соответствующих экспериментов подтвердили преимущества такой раскладки, но, несмотря на это, она так и не появилась на клавиатуре пишущих машинок. Между тем изобретение компьютеров и последующие их усовершенствования должны были вновь привлечь внимание к проблеме раскладки. Однако этого не произошло. Инертность и консерватизм человеческого мышления способствовали тому, что QWERTY успешно перебралась и на клавиатуры компьютеров, с каждым днем все более и более укрепляя свои позиции. Ныне даже трудно поверить в то, что когда-нибудь по тем или иным причинам она уступит место какому-либо своему конкуренту. Тем не менее для английского языка проблема “оптимальной” раскладки символов на клавиатуре компьютера остается нерешенной. Продвижение в этом направлении уже имеется. П. Клауслер – пПрограммист из фирмы Cray (США) – П. Клауслер недавно обнародовал свой подход к решению проблемы для английской клавиатуры1. Им предложена алгоритмическая процедура для вычисления “суммарной работы”, затрачиваемой на набор текста фиксированной длины (порядка 20 Mb) для заданной раскладки символов на клавиатуре. Из 4096 случайно выбранных раскладок предпочтение отдается той, для которой принятый критерий качества принимает наименьшее значение. Определенная таким образом приоритетная раскладка оказывается также более эффективной в сравнении с раскладками QWERTY и Дворака. В методическом подходе Клауслера просматриваются 2 два узких места: · нет статистического обоснования того, что случайная выборка из 4096 раскладок является репрезентативной; следовательно, полученный им результат нельзя принимать как окончательный; · достаточно субъективной представляется совокупность количественных показателей, введенных эвристическим путем для характеристики элементарных работ, затрачиваемых на нажатие той или иной клавиши; по этой причине нет никакой уверенности в том, что окончательный результат является устойчивым по отношению к слабым изменениям упомянутых количественных показателей. Отмеченные недостатки указывают на незавершенность имитационной модели Клауслера даже для теоретического решения вопроса об оптимальной раскладке латинских букв на английской клавиатуре. В заключение обзора обратим внимание на характер раскладки букв русского алфавита на пишущей машинке (ГОСТ 6431-90) и компьютерной клавиатуре (ГОСТ 14289-88, стандарт для среды MS DOS и стандарт для среды MS Windows)2. Различия этих случаев наблюдаются в позициях управляющих, цифровых, функциональных, символьных и прочих клавишей на клавиатуре. Что касается раскладки букв, то она абсолютно одинакова для них и представляется достаточно обоснованной. В упомянутой ссылке, однако, не содержится описания того, какие принципы были положены в основу такой раскладки. В настоящей статье, непосредственно продолжающей исследования, начатые в [1]материале, опубликованном в 2003 г. в № 3 настоящего журнала, предлагается критерий для оптимальной раскладки символов на компьютерной клавиатуре. Формализация критерия. Пусть K – конечное множество, состоящее из n клавишей
Пусть A – конечный набор символов
Известно, что n символов на n клавишах можно расположить n! различными способами. Возможные варианты раскладок будем записывать в виде подстановки n-й степени:
указывая тем самым, на каких клавишах размещаются те или иные символы. Здесь
где Критерий раскладки. Из всех возможных раскладок предпочтение следует отдать той, для которой В настоящей статье получен следующий результат. Теорема. В условиях (1) и (2) на раскладке
Иными словами, это значит, что наилучшей является такая раскладка, в которой чаще встречающиеся символы размещаются на менее трудоемких клавишах и наоборот. Замечание 1. Отметим, что если бы нас интересовал вопрос о наихудшей раскладке символов по клавишам компьютерной клавиатуры, то таковой оказывается
В такой раскладке, очевидно, чаще встречающиеся символы располагаются на самых трудоемких клавишах, а редкие символы – на легко доступных клавишах. Замечание 2. В случае если число m клавиш оказывается больше числа n символов, то исходный набор символов A можно пополнить фиктивными символами Доказательство теоремы осуществляется методом математической индукции. Вначале утверждение теоремы проверяется для n=2. В этом случае имеются всего лишь две раскладки
вследствие условий (1) и (2). Теперь предположим, что теорема верна при n=s. Это значит, что раскладка
Докажем теорему для значения n=s+1, то есть установим, что раскладка Будем говорить, что две раскладки совпадают по одному символу, если у них на одной и той же клавише размещается один и тот же символ. Разобьем множество {Р(аK1, аK2, …, аK(s+1))} всевозможных раскладок s+1 символа по s+1 клавишам на два подмножества Проверим, что для любой раскладки из подмножества
В самом деле, пусть
– одна из таких раскладок, которая совпадает с наилучшей по символу
то есть суммарная работа на печатание R-текста на клавиатуре с раскладкой из подмножества Теперь обратимся к подмножеству
Сопоставим ей следующую раскладку
которая отличается от предыдущей всего лишь транспозицией символов
в силу (1) и (2). Однако раскладка Теорема доказана. Замечание 3. По аналогии с приведенным доказательством устанавливается справедливость утверждения, высказанного в замечании 1. Как было сказано ранее, раскладка английского алфавита по клавишам компьютерной клавиатуры не является оптимальной. Однако подобная ситуация имеет место для большинства европейских языков, в основу которых положен латинский алфавит. Настоящая работа, в части приложения, адресуется прежде всего тем естественным языкам, для которых еще не утверждены национальные стандарты компьютерной клавиатуры. На пути практического применения полученных результатов необходимо определить объем репрезентативного текста и значения частот Интересно отметить, что предварительные исследования, проведенные для английского, русского и таджикского языков, показали, что приблизительно 25 страниц случайной выборки текстов во всех случаях являются репрезентативными, статистическая обработка которых позволяет подсчитать достаточно точно значения частот встречаемости букв. Еще одна группа параметров, влияющая на выбор оптимальной раскладки символов на клавиатуре, – элементарные работы Очевидно, что вместо метода экспертных оценок могут быть использованы и другие методы. Однако какой бы из них не был применен, полезно будет провести исследование устойчивости оптимальной раскладки в зависимости от вариации значений
В случае, если для пары клавиш, например |
http://swsys.ru/index.php?id=597&lang=%29&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Методы восстановления пропусков в массивах данных
- Интеллектуальные хранилища данных в системах государственного управления
- Методы поисковой адаптации на основе механизмов генетики, самообучения и самоорганизации

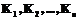 , причем каждой клавише
, причем каждой клавише 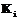 приписано некоторое положительное число
приписано некоторое положительное число 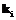 , указывающее количество элементарной работы, которую следует затратить для того, чтобы “активизировать”
, указывающее количество элементарной работы, которую следует затратить для того, чтобы “активизировать” 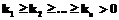 . (1)
. (1)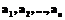 (например, буквы какого-либо естественного языка L и, возможно, некоторые знаки препинания), предназначенных для раскладки на клавишах множества K. Предположим, что нам известны частоты
(например, буквы какого-либо естественного языка L и, возможно, некоторые знаки препинания), предназначенных для раскладки на клавишах множества K. Предположим, что нам известны частоты 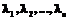 встречаемости этих символов в репрезентативных текстах (R-текстах), написанных на языке L, причем без ограничения общности можем принять условие
встречаемости этих символов в репрезентативных текстах (R-текстах), написанных на языке L, причем без ограничения общности можем принять условие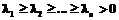 . (2)
. (2)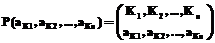 ,
, может быть любым символом из набора A, при этом
может быть любым символом из набора A, при этом 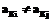 , если
, если 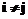 . Сопоставим каждому варианту количественный показатель
. Сопоставим каждому варианту количественный показатель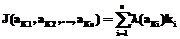 ,
,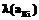 – частота встречаемости того символа, который в данном варианте присваивается клавише
– частота встречаемости того символа, который в данном варианте присваивается клавише  .
. принимает минимальное значение.
принимает минимальное значение.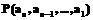 суммарная работа, затрачиваемая на набор репрезентативного текста, имеет минимальное значение:
суммарная работа, затрачиваемая на набор репрезентативного текста, имеет минимальное значение: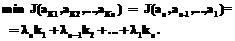
 , причем ей соответствует наибольшая суммарная затрачиваемая работа на набор R-текста:
, причем ей соответствует наибольшая суммарная затрачиваемая работа на набор R-текста: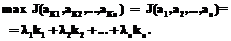
 , приписав им нулевые частоты встречаемости ln+1=ln+2 =…=lm= =0. После этого можно воспользоваться результатами теоремы.
, приписав им нулевые частоты встречаемости ln+1=ln+2 =…=lm= =0. После этого можно воспользоваться результатами теоремы.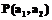 и
и 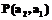 , причем именно вторая, как это утверждается в теореме, является наилучшей, поскольку
, причем именно вторая, как это утверждается в теореме, является наилучшей, поскольку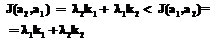
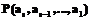 является наилучшей и
является наилучшей и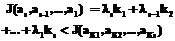 .
. является наилучшей.
является наилучшей.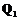 и
и 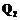 . В состав
. В состав  .
.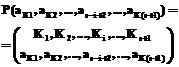 –
–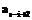 , размещенному на клавише
, размещенному на клавише 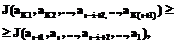
 ), на которой размещается символ
), на которой размещается символ 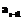 (с наименьшей частотой встречаемости):
(с наименьшей частотой встречаемости):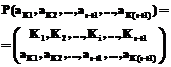 .
. ,
,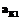 . Сравнивая суммарные работы, выполняемые на этих раскладках, получим
. Сравнивая суммарные работы, выполняемые на этих раскладках, получим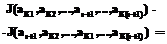
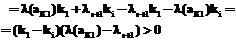
 принадлежит подмножеству
принадлежит подмножеству 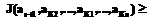
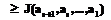 . Но тогда и
. Но тогда и 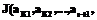
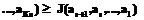 , то есть затраты суммарной работы на печатание R-текста на любой раскладке из
, то есть затраты суммарной работы на печатание R-текста на любой раскладке из 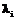 встречаемости букв (возможно, и некоторых знаков препинания) в текстах, написанных на интересующем нас языке. Для этих целей подготавливается выборка из 100-150 случайно взятых страниц, которая, вероятнее всего, окажется достаточной для получения достоверных результатов. Затем с шагом в 5 страниц осуществляется обработка все возрастающего объема случайной выборки и контролируется процесс сходимости частот встречаемости символов. Начиная с некоторого объема, вариации функции распределения частот практически прекращаются, и последующая обработка становится бессмысленной. Случайную выборку такого объема следует рассматривать как репрезентативную, а извлекаемые из нее частоты встречаемости символов их окончательными значениями.
встречаемости букв (возможно, и некоторых знаков препинания) в текстах, написанных на интересующем нас языке. Для этих целей подготавливается выборка из 100-150 случайно взятых страниц, которая, вероятнее всего, окажется достаточной для получения достоверных результатов. Затем с шагом в 5 страниц осуществляется обработка все возрастающего объема случайной выборки и контролируется процесс сходимости частот встречаемости символов. Начиная с некоторого объема, вариации функции распределения частот практически прекращаются, и последующая обработка становится бессмысленной. Случайную выборку такого объема следует рассматривать как репрезентативную, а извлекаемые из нее частоты встречаемости символов их окончательными значениями. .
.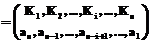
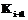 , соответствующие им трудоемкости оказываются равными (
, соответствующие им трудоемкости оказываются равными (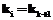 ), то, по крайней мере, имеются две оптимальные раскладки (они различаются тем, что в них символы
), то, по крайней мере, имеются две оптимальные раскладки (они различаются тем, что в них символы 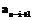 и
и 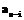 , размещаемые соответственно на
, размещаемые соответственно на