Генетический алгоритм оптимизации структуры лингвистических переменных при построении баз знаний нечетких систем
| Язенин А.В. () - , Панфилов С.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
В статье рассматривается метод построения терм-множеств лингвистических переменных по заданному обучающему сигналу, основанный на информационном анализе совместной плотности распределения элементов терм-множества лингвистической переменной. Предложенный способ позволяет определить тип и необходимое количество элементов терм-множества, что дает возможность применить к полученной структуре известные методы оптимизации. Разработан метод кодирования параметров, определяющих структуру терм-множества, позволяющий использовать генетический алгоритм с фиксированной длиной хромосом для оптимизации. Кратко обсуждаются результаты моделирования построения лингвистических переменных для типового обучающего сигнала.
Рассмотрим обучающий сигнал и его лингвистическое описание, представленные на рисунке 1. Обучающий сигнал разделен на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В общем виде каждый из участвующих сигналов является выбранной траекторией некоторого случайного процесса. При этом подразумевается, что в каждый момент времени существует некоторая зависимость между входными и выходными сигналами. Например, в случае аппроксимации некоторого управляющего сигнала входными компонентами могут являться ошибка управления и ее производная, а выходным компонентом – требуемое значение управляющего воздействия либо некоторые настраиваемые параметры системы управления. На рисунке 1 зависимости между сигналами представлены графически горизонтальными и вертикальными линиями. Каждой из компонент сигнала соответствует некоторая лингвистическая переменная, описывающая сигнал с помощью лингвистического значения сигнала и соответствующего терм-множества. Мощность терм-множества и параметры составляющих его элементов (класс и параметры функции принадлежности) неизвестны. "Полноту" лингвистического описания сигнала можно описать на уровне взаимосвязи терм-множеств, входящих в лингвистические переменные. На рисунке 1 эти взаимосвязи представлены вертикальными и горизонтальными линиями, соединяющими терм-множества лингвистических переменных. Увеличение мощности терм-множеств ведет к увеличению числа возможных линий связи между элементами терм-множества лингвистических переменных. В результате этого большему числу состояний сигнала будут соответствовать более точные лингвистические значения. В пределе, если мощность терм-множеств бесконечна, лингвистическое описание будет точно соответствовать числовым значениям. Меньшее число терм-множеств и, соответственно, вертикальных связей огрубляет лингвистическое описание, что в большинстве случаев предпочтительнее с точки зрения увеличения робастности системы. Определение требуемого соотношения между точностью описания и необходимой робастностью является очень важной задачей и на практике решается экспертными методами. Важно также отметить, что горизонтальные линии, соединяющие элементы терм-множеств разных лингвистических переменных, по сути являются компонентами продукционных правил, на основании которых лингвистическое описание связывается в систему нечеткого вывода. Таким образом, выбор структуры лингвистических переменных косвенно влияет на объем и адекватность получаемой базы продукционных правил. В статье рассмотрен информационный подход к оптимизации структуры лингвистических переменных. Данный подход является развитием результатов, представленных в [2], применительно к оптимизации нечетких систем. Приводятся результаты численного моделирования при построении лингвистических переменных для некоторых обучающих сигналов. Рассмотрим типичное продукционное правило системы нечеткого вывода Сугено нулевого порядка: IF x1 is Результирующий вывод по M нечетким правилам указанного типа вычисляется по формуле: F(x1, x2, … xn) = Рассмотрим обучающий сигнал, представленный выборкой: [x(t), y(t)], где t=1,…,N – порядковый номер элемента выборки; N – число элементов в выборке; x(t) = (x1(t), …, xm(t)) – компоненты входной составляющей обучающего сигнала; y(t)=(y1(t),…,yn(t)) – компоненты выходной составляющей обучающего сигнала; m, n – число входных и выходных компонент сигнала соответственно. Задача состоит в определении оптимального лингвистического описания сигналов. В качестве критерия оптимальности используется функция максимума вероятности вхождения компонент сигнала в различные элементы терм-множества лингвистической переменной при минимальной мощности терм-множества, описывающего каждую компоненту сигнала. Перейдем к формальному описанию задачи. Определим лингвистические переменные для системы (1). Лингвистическая переменная описывается следующими элементами: (X,T(X),U,G,M), где X – название лингвистической переменной; T(X) – терм-множество лингвистической переменной X, определенной в U; U – универсум (диапазон изменения сигналов, на котором определены функции принадлежности), в общем случае нормированный на единицу; G – синтаксическое правило для генерации имен X; M – семантическое правило, задающее интерпретацию лингвистических значений. Для представления всех m+n элементов, входящих в обучающую выборку, необходимо определить m+n лингвистических переменных. Пусть [X,Y], X=(X1,…,Xm) и Y=(Y1,…,Yn) есть набор лингвистических переменных, соответствующих входным и выходным составляющим обучающего сигнала. Тогда для каждой лингвистической переменной можно задать некоторое терм-множество. В результате вход-выход системы может быть представлен в следующем виде: X1: Y1: Здесь На первоначальном этапе формирования базы знаний класс функций принадлежности и их параметры неизвестны. Неизвестны также мощности l(.) терм-множеств соответствующих лингвистических переменных. Предположим, что l(.) является параметром, оптимизируемым некоторым генетическим алгоритмом, с диапазоном поиска: Имея в результате оптимизации значения l(.), можно построить равновероятностное распределение {
Данное ограничение подобно разделению гистограммы сигнала на криволинейные трапеции одинаковой площади. При этом основания криволинейных трапеций задают носители соответствующих функций принадлежности. Пересечение двух соседних элементов терм-множества может задаваться некоторым коэффициентом, который является результатом работы генетического алгоритма. Этот коэффициент принимает значение 0 при пустом пересечении и больше нуля, когда пересечение не пусто. На рисунке 2 представлены варианты размещения треугольных функций принадлежности согласно введенному ограничению для одного компонента обучающего сигнала, гистограмма которого представлена на рисунке 2г. Модальные значения несимметричных нечетких мно- жеств помещаются в наиболее вероятную точку, попадающую в основание криволинейной тра- пеции. Взаимосвязь между возможностью активации нечеткого множества в зависимости от значений его параметров можно выразить через вероятность его активации:
Исходя из геометрических соображений, совместную вероятность активации одновременно двух нечетких множеств можно рассчитать по формуле:
где * обозначает выбранную логическую операцию нечеткого «И», или T-норму [3]; j=1,…,lXi, l=1,..,lXk – индексы соответствующих функций принадлежности. Если i=k и j¹l, выражение (4) определяет “вертикальные связи”; если i¹k – “горизонтальные связи”. Мерой “вертикальных” и “горизонтальных” связей является совместная вероятность попадания значений сигнала в нечеткие множества, определяющие соответствующую связь. Набор значений лингвистических переменных оптимален, если суммарная мера горизонтальных связей максимальна при минимальном значении суммарной меры вертикальных связей. Таким образом, можно определить функцию пригодности генетического алгоритма, оптимизирующего число и параметры функций принадлежности как максимум меры (4) с учетом ограничения (2). Для формирования системы оптимизации была принята следующая структура хромосомы:
Другой способ задания функций пригодности (3) и (4) может быть основан на энтропии Шеннона. В этом случае формулы (3) и (4) могут быть представлены в следующем виде:
и
В некоторых приложениях можно использовать комбинацию информационных и вероятностных мер. Результатом работы генетического алгоритма является оптимизированная структура терм-множеств лингвистических переменных. Структура генетического алгоритма Генетические алгоритмы являются процедурами поиска глобального оптимума (максимума или минимума) некоторой целевой функции, основанными на принципах естественной эволюции. В них сгенерированная случайным образом начальная популяция решений подвергается воздействию генетических операций, таких как селекция, скрещивание и мутация [4,5]. В результате получается новая популяция решений с улучшен- ными основными свойствами (значениями це- левой функции). Данный процесс продолжа- ется итеративно до достижения глобального оптимума. Генетический алгоритм, имеющий хромосому (5), может быть любым из известных генетических алгоритмов, имеющих хромосому фиксированной длинны. В данной работе был выбран генетический алгоритм «элитного» типа с двухточечными операциями скрещивания и мутации. В качестве системы кодирования была выбрана бинарная система с числом бит для кодирования каждого параметра, достаточным для покрытия соответствующего диапазона изменения. Для более компактного размещения гены представлены символьными типами данных (16 бит на символ), при этом были использованы операции прямого копирования содержимого памяти для реализации операций скрещивания и мутации. Модельный пример Рассмотрим некоторый гармонический сигнал, имеющий два входа и один выход. Задачей является определение структуры и параметров системы нечеткого вывода, аппроксимирующей данный сигнал с минимальной ошибкой аппроксимации. Аппроксимация гармонических сигналов с помощью систем нечеткого вывода является очень важной задачей во многих приложениях теории управления. В данном примере первым входом системы нечеткого вывода является некоторая синусоидальная волна. В качестве второго входа взят тот же самый сигнал, но с фазовым сдвигом в
1) с помощью генетического алгоритма; 2) с помощью алгоритма обратного распространения ошибки, примененного к случайно заданным параметрам; 3) с помощью алгоритма обратного распространения ошибки с начальными условиями, определенными генетическим алгоритмом. Для проведения сравненительного анализа, была также создана база знаний с помощью коммерчески доступной нечеткой нейронной сети AFM [6]. Результаты аппроксимации с применением трех указанных методик представлены в таблице. Применение генетического алгоритма для получения начальных условий для метода обратного распространения ошибки значительно улучшило производительность нечеткой нейронной сети, а также ускорило в два раза сходимость алгоритма оптимизации. Таблица Результаты аппроксимации гармонического сигнала
Для проверки разработанного подхода был рассмотрен также типовой обучающий сигнал Фишера [7]. Для компонент сигнала были получены лингвистические аппроксимации и сформирована база нечетких правил. В процессе обучения было использовано 50 % данных. В результате получено 100 % распознавание элементов обучающей выборки, и 97 % распознавание элементов тестирующей выборки. В статье разработаны алгоритмы формирования нечетких лингвистических данных для некоторых классов обучающих сигналов. Проведенные численные расчеты на модельном примере показали эффективность предложенного подхода при формировании количественных параметров лингвистических переменных. Данный подход внедрен в систему автоматического формирования структур баз знаний систем нечеткого вывода и является компонентом, формирующим начальную базу знаний системы. Разработанные методы могут быть применены как к решению задач классификации, так и задач интеллектуального управления динамическими объектами. Список литературы 1. Лохин В.М., Макаров И.М., Манько С.В., Романов М.П. Методические основы аналитического конструирования регуляторов нечеткого управления. - Изв. РАН: Теория и системы управления. - 2000. - №1. - С. 56-69. 2. Torkkola K. Mutual Information in Learning Feature Transformations, Proc. 17th International Conf. on Machine Learning, 2000. 3. Nguyen H.N., Walker E.A. A First Course in Fuzzy Logic, CRC Press, 1997. 4. Holland J., Adaptation in Natural and Artificial Systems, Univercity of Michgan (1975), reprinted with revision by MIT Press (1992). 5. David E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley Pub Co., 1989. 6. Adaptive Fuzzy Modeler (AFM), http://eu.st.com/stonline/index.shtml. 7. Fisher R.A. The Use of Multiple Measurements in Axonomic Problems, Annals of Eugenics 7, 1936, pp. 179-188. |
http://swsys.ru/index.php?id=599&lang=%E2%8C%A9%3Den&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:

 Построение терм-множеств лингвистических переменных является важным этапом формирования баз знаний нечетких систем, и в особенности, нечетких регуляторов. Структура терм-множества лингвистической переменной характеризуется числом и типом функций принадлежности, определяющих элементы терм-множества данной переменной. В обычной практике создания баз знаний нечетких систем построение терм-множества осуществляется экспертом на основании личного опыта либо путем итеративного подбора оптимальной структуры [1]. Обычно в качестве критерия оптимальности выступает значение ошибки аппроксимации, вычисляемое как разница между желаемым значением выходного сигнала и значением, полученным в результате нечеткого вывода на заключительном этапе оптимизации параметров структуры нечеткой системы. Таким образом, известные алгоритмы оптимизации должны быть применены итеративно к разным (изначально заданным) структурам лингвистических переменных. Затем полученные результаты сравниваются, и выбирается наилучший вариант. Данный процесс требует больших вычислительных затрат, связанных с применением алгоритмов оптимизации, и во многих случаях (особенно при сложной структуре проектируемого регулятора) остается значительная вероятность появления ошибки второго рода, связанной с неоптимальной изначальной структурой терм-множеств лингвистических переменных.
Построение терм-множеств лингвистических переменных является важным этапом формирования баз знаний нечетких систем, и в особенности, нечетких регуляторов. Структура терм-множества лингвистической переменной характеризуется числом и типом функций принадлежности, определяющих элементы терм-множества данной переменной. В обычной практике создания баз знаний нечетких систем построение терм-множества осуществляется экспертом на основании личного опыта либо путем итеративного подбора оптимальной структуры [1]. Обычно в качестве критерия оптимальности выступает значение ошибки аппроксимации, вычисляемое как разница между желаемым значением выходного сигнала и значением, полученным в результате нечеткого вывода на заключительном этапе оптимизации параметров структуры нечеткой системы. Таким образом, известные алгоритмы оптимизации должны быть применены итеративно к разным (изначально заданным) структурам лингвистических переменных. Затем полученные результаты сравниваются, и выбирается наилучший вариант. Данный процесс требует больших вычислительных затрат, связанных с применением алгоритмов оптимизации, и во многих случаях (особенно при сложной структуре проектируемого регулятора) остается значительная вероятность появления ошибки второго рода, связанной с неоптимальной изначальной структурой терм-множеств лингвистических переменных. AND x2 is
AND x2 is  AND … AND xn is
AND … AND xn is  THEN y=r(l).
THEN y=r(l). . (1)
. (1) ,…, Xm:
,…, Xm: ;
; ,…, Yn:
,…, Yn: .
. , i=1,…,m, ji=1,…,lXi – терм-множество, соответствующее i-й компоненте входного сигнала;
, i=1,…,m, ji=1,…,lXi – терм-множество, соответствующее i-й компоненте входного сигнала;  , i=1,…,n, ji=1,…,lYi – терм-множество, соответствующее i-й компоненте выходного сигнала.
, i=1,…,n, ji=1,…,lYi – терм-множество, соответствующее i-й компоненте выходного сигнала. Î[1,Lmax], i=1,…,m,
Î[1,Lmax], i=1,…,m,  Î[1,Lmax], i=1,…,m. Lmax является максимально допустимым числом элементов терм-множества. На практике значение Lmax определяется экспертным путем.
Î[1,Lmax], i=1,…,m. Lmax является максимально допустимым числом элементов терм-множества. На практике значение Lmax определяется экспертным путем. }, характеризующее принятие i-й компонентой обучающего значения в соответствующем терм-множестве. При этом выполняется условие:
}, характеризующее принятие i-й компонентой обучающего значения в соответствующем терм-множестве. При этом выполняется условие: , i=1,…,m, j=1,...,
, i=1,…,m, j=1,..., . (3)
. (3)
 (4)
(4)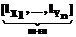
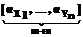
 . (5)
. (5) В формуле (5) l(.)Î[1,Lmax] – гены, кодирующие мощности терм-множеств лингвистических переменных; a(.)Î[0,1] – гены, кодирующие коэффициенты, характеризующие пересечения носителей функций принадлежности соответствующей лингвистической переменной Xi(Yi); T(.) – гены, кодирующие класс функций принадлежности нечетких множеств.
В формуле (5) l(.)Î[1,Lmax] – гены, кодирующие мощности терм-множеств лингвистических переменных; a(.)Î[0,1] – гены, кодирующие коэффициенты, характеризующие пересечения носителей функций принадлежности соответствующей лингвистической переменной Xi(Yi); T(.) – гены, кодирующие класс функций принадлежности нечетких множеств. (3a)
(3a) (4a)
(4a) . В качестве выходного сигнала взят сигнал, равный произведению квадратов входных сигналов:
. В качестве выходного сигнала взят сигнал, равный произведению квадратов входных сигналов: ,
, ,
,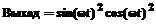 .
. Аппроксимация гармонических сигналов обычно требует достаточно большой мощности каждой лингвистической переменной и большого числа нечетких правил. Для аппроксимации взятого сигнала была выбрана нечеткая модель Сугено нулевого порядка. Генетический алгоритм определил и распределил 9 треугольных функций принадлежности для каждого из входных сигналов. На рисунках 3 и 4 представлены полученные лингвистические переменные для первого и второго входов соответственно. После создания базы правил и удаления неактивизируемых правил база составила 56 из 81 возможного правила.
Аппроксимация гармонических сигналов обычно требует достаточно большой мощности каждой лингвистической переменной и большого числа нечетких правил. Для аппроксимации взятого сигнала была выбрана нечеткая модель Сугено нулевого порядка. Генетический алгоритм определил и распределил 9 треугольных функций принадлежности для каждого из входных сигналов. На рисунках 3 и 4 представлены полученные лингвистические переменные для первого и второго входов соответственно. После создания базы правил и удаления неактивизируемых правил база составила 56 из 81 возможного правила.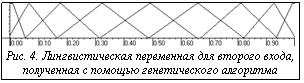 После создания функций принадлежности были созданы 3 базы правил с применением нескольких методик оптимизации параметров модели Сугено:
После создания функций принадлежности были созданы 3 базы правил с применением нескольких методик оптимизации параметров модели Сугено: