Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм численного решения задач вариационного исчисления на основе самоорганизующейся нечеткой нейронной сети
Аннотация:
Abstract:
| Авторы: Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 14552 |
Версия для печати Выпуск в формате PDF (1.06Мб) |
При построении оптимальных систем управления приходится решать задачи двух видов: синтез оптимальных алгоритмов управления (оптимальных управляющих воздействий) и синтез законов управления [1]. В настоящее время разработано большое количество различных алгоритмов численного решения указанных задач, которые базируются на классическом математическом аппарате [2]. Применение нечеткой логики в данных алгоритмах позволяет, с одной стороны, использовать априорную информацию об искомом решении, что повышает его точность, и с другой – получать результаты в виде продукционных правил если–то, которые затем легко интерпретировать, что дает возможность использовать данные алгоритмы в человеко-машинных системах (например, системах поддержки принятия управленческих решений) [3]. Рассмотрим задачу синтеза системы нечеткого логического вывода, реализующую функцию
которая обращает в минимум некоторый нелинейный функционал Классическим алгоритмом решения задачи является применение нечетких нейронных сетей, например, сетей Ванга-Менделя [3]. При этом стандартные алгоритмы обучения, основанные на обратном распространении ошибки, в данном случае неприменимы, так как в общем случае неизвестен гессиан связи функционала В данной ситуации можно применять алгоритмы наращивания (АН) сети, в которых чередуются циклы обучения сети и добавления новых правил. Однако, как известно, АН сети работают крайне медленно [5]. Рассмотрим алгоритм адаптации нечеткой нейронной сети, как представляется, свободный от указанных недостатков. Допустим, что о зависимости (1) имеется априорная информация, записанная в виде совокупности m0 нечетких продукционных правил вида: Пr: если х1 есть Аr1 и х2 есть Аr2 и … и хn есть Аrn, то у = уr, где r =1, 2, … m0 – номер правила в базе знаний, xj (j=1, 2, …, n) – компоненты вектора Отметим, что данная априорная информация может и отсутствовать (при этом m0 = 0). Предположим далее, что может быть реализован эксперимент, заключающийся в определении значения функционала Алгоритм состоит в реализации последовательности следующих шагов. Шаг 0 (предварительный). Задается e – погрешность нахождения минимума функционала. Задается априорная база нечетких правил. Устанавливается текущее число правил в базе знаний m=m0. Шаг 1. Если формируемая база знаний пуста, переход к шагу 2, иначе с помощью алгоритма нечеткого вывода Сугэно 0-го порядка с использованием имеющихся продукционных правил определяется оценка [3, 5]:
где По оценке Шаг 2. База знаний пополняется правилом вида: Пm+1: если х1 есть А(m+1)1 и х2 есть А(m+1)2 и … хn есть А(m+1)n, то
где По формуле, аналогичной (2), определяется оценка Шаг 3. Проверяется неравенство:
где Значение m модифицируется: m:=m+1. При невыполнении неравенства (4) переход к шагу 2, иначе переход к шагу 4. Шаг 4. База знаний считается сформированной. В качестве окончательной берется база знаний, состоящая из Рассмотренный алгоритм будем называть далее нечетким дополняюще-оптимизирующим алгоритмом (ДОА). Оценим эффективность ДОА по сравнению с АН нечеткой нейронной сети. Под эффективностью алгоритма будем понимать следующее: пусть выделено N вычислений функционала Допустим, что объем вычислений при настройке нечеткой нейронной сети приблизительно прямо пропорционален числу настраиваемых параметров [3]. Напомним, что в АН происходит оптимизация параметров всех правил, затем добавление нового правила и снова оптимизация параметров всех правил [5]. Число вычислений функционала в АН приблизительно определяется формулой:
где Формулу (5) можно привести к виду:
Для ДОА при каждом добавлении нового продукционного правила оптимизируется только Число вычислений для ДОА определяется формулой:
На рисунке 1 построены графики зависимости, определенные по формулам (6) и (7) соответственно, для случая, когда
На практике приведенные оценки являются лишь приближенными. Во-первых, база знаний сгенерированная с помощью ДОА, получается обычно больше, чем при использовании АН, что несколько снижает эффективность ДОА. Во-вторых, с ростом числа переменных число вычислений растет обычно быстрее, чем линейная зависимость, что, наоборот, говорит в пользу эффективности ДОА. Рассмотрим иллюстрирующий пример. Пусть имеется система, приведенная на рисунке 2.
Примем следующие обозначения: M – амплитудно-импульсный модулятор с фиксатором нулевого порядка и периодом квантования Т0=0,2; НЭ – нелинейный элемент – статическая нелинейность, определяемая формулой:
На вход системы подается сигнал:
Задача состоит в нахождении нелинейной функции
Для решения задачи использовались разработанный ДОА с
В результате работы алгоритмов были сгенерированы продукционные правила вида: Пr: если где r – номер правила,
С помощью ДОА и АН до выполнения условия останова было сгенерировано 5 и 4 нечетких продукционных правила соответственно. Ниже приведены параметры, нечетких продукционных правил, сгенерированных с помощью ДОА:
и АН:
Результаты моделирования сведены в таблице. Из таблицы видно, что при увеличении количества правил объем вычислений в алгоритме наращивания лавинообразно возрастает, что приводит к невозможности найти точку глобального минимума за выделенное число итераций и к обрыву процесса (выполнению критерия останова). В ДОА объем вычислений растет приблизительно линейно с ростом количества сгенерированных правил.
Видно, что при равном N значения функционала при применении ДОА всегда меньше, чем при применении АН, что показывает преимущество разработанного алгоритма. Список литературы 1. Мирошник И.В., Никифоров В.О., Фрадков А.Л. Нелинейное и адаптивное управление сложными динамическими системами. - СПб.: Наука, 2000. 2. Федоренко Р.П. Приближенное решение задач оптимального управления. - М.: Наука, 1978. 3. Осовский С. Нейронные сети для обработки информации. - М.: Финансы и статистика, 2002. 4. Омату С., Халид М., Юсоф Р. Нейроуправление и его приложения. Кн.2 / Общ. ред. А.И. Галушкина. - М.: ИРПЖР, 2000. 5. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Горячая линия – ТЕЛЕКОМ, 2001. 6. Дьяконов В.П., Круглов В.В. Математические пакеты расширения MATLAB: Специальный справочник. - СПб.: Питер, 2001. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=616&page=article |
Версия для печати Выпуск в формате PDF (1.06Мб) |
| Статья опубликована в выпуске журнала № 4 за 2003 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Подход к выбору оптимального маршрута при перевозке крупногабаритных грузов на основе нейросетевых технологий
- Методы восстановления пропусков в массивах данных
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Автоматизированная информационная система маркетолога
- Метод интегрированного описания топологических отношений в геоинформационных системах
Назад, к списку статей



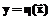 , (1)
, (1) , заданный в общем случае неявно, то есть
, заданный в общем случае неявно, то есть  – лишь абстрактное обозначение, выражающее принципиальную возможность определения I, зная
– лишь абстрактное обозначение, выражающее принципиальную возможность определения I, зная  . Используя метод штрафных функций, к данной задаче можно свести большинство задач с ограничениями [2].
. Используя метод штрафных функций, к данной задаче можно свести большинство задач с ограничениями [2]. и весов нечеткой сети [4]. Кроме того, существенным недостатком традиционных нечетких сетей является необходимость априорного выбора числа продукционных правил [3].
и весов нечеткой сети [4]. Кроме того, существенным недостатком традиционных нечетких сетей является необходимость априорного выбора числа продукционных правил [3]. , Arj – некоторые нечеткие числа, имеющие функции принадлежности
, Arj – некоторые нечеткие числа, имеющие функции принадлежности  .
. при текущем виде зависимости
при текущем виде зависимости  .
. , (2)
, (2) – степень истинности предпосылок r-го правила.
– степень истинности предпосылок r-го правила. определяется значение функционала
определяется значение функционала  .
. , где
, где  – нечеткие числа с треугольными функциями принадлежности [3, 5]:
– нечеткие числа с треугольными функциями принадлежности [3, 5]: (3)
(3) – центры нечетких чисел
– центры нечетких чисел  .
.
 . Настраиваются параметры
. Настраиваются параметры  , …
, …  ,
,  ,
,  , …
, …  путем оптимизации функции Im+1=
путем оптимизации функции Im+1= 

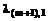
 по данным параметрам [3].
по данным параметрам [3]. , (4)
, (4) ,
,  .
. продукционных правил. В качестве оптимального значения функционала выбирается
продукционных правил. В качестве оптимального значения функционала выбирается  , (5)
, (5) – const;
– const;  – число настраиваемых параметров в одном продукционном правиле;
– число настраиваемых параметров в одном продукционном правиле;  . (6)
. (6) параметров.
параметров. . (7)
. (7) и
и  .
.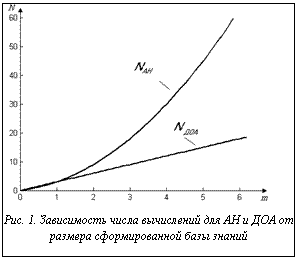 Из рисунка видно, что ДОА требует значительно меньше вычислений по сравнению с АН.
Из рисунка видно, что ДОА требует значительно меньше вычислений по сравнению с АН.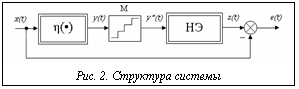
 .
.
 , минимизирующей функционал:
, минимизирующей функционал: .
. и алгоритм наращивания нечеткой сети. В качестве алгоритма параметрической оптимизации применялся алгоритм Нелдера-Меада из пакета MATLAB 6.5 (R13) [6]. Для уменьшения вероятности сходимости процесса к локальному экстремуму алгоритм запускался 10 раз из случайно задаваемых начальных точек с последующим выбором наилучшего решения.
и алгоритм наращивания нечеткой сети. В качестве алгоритма параметрической оптимизации применялся алгоритм Нелдера-Меада из пакета MATLAB 6.5 (R13) [6]. Для уменьшения вероятности сходимости процесса к локальному экстремуму алгоритм запускался 10 раз из случайно задаваемых начальных точек с последующим выбором наилучшего решения. На рисунке 3 показаны входной сигнал
На рисунке 3 показаны входной сигнал  и сигнал на выходе НЭ
и сигнал на выходе НЭ  (см. рис. 2) после окончания работы ДОА.
(см. рис. 2) после окончания работы ДОА. есть
есть  , то
, то  ,
,













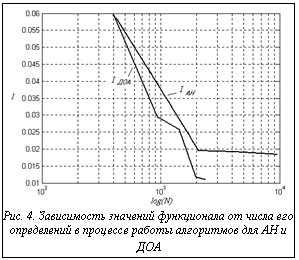
 На рисунке 4 показаны зависимости значений функционала (IАН – для АН и IДОА – для ДОА) от числа его определений в процессе работы алгоритмов.
На рисунке 4 показаны зависимости значений функционала (IАН – для АН и IДОА – для ДОА) от числа его определений в процессе работы алгоритмов.