Современные системы безопасности химических производств являются сложными человеко-машинными системами, которые можно подразделить на взаимосвязанные подсистемы с иерархической структурой, состоящей из нескольких уровней иерархии.
Современная технология создания систем управления обеспечения безопасности химических производств предполагает построение систем, имеющих повышенную живучесть (гибкость, маневренность, адаптивность, самоорганизуемость, оперативность, конкурентоспособность и т.д.), на основе ее рациональной организации в органической связи с системой принятия решений (СПР) в условиях изменяющейся окружающей среды.
Распознавание неисправностей и аварийных состояний в соответствии с принципом иерархичности начинается с изучения режима протекания процесса в аппарате и определение его состояния. Диагноз состояния технологического процесса осуществляется на основе дискретных моделей реакторных узлов, которые были получены линеаризацией основных уравнений материальных и тепловых балансов для нормального режима работы на основе метода разделения состояний химико-технологической системы (ХТС). Нарушение ограничений в дискретных моделях реакторных узлов говорит о появлении неисправности в технологии.
Суть метода разделения состояний ХТС такова. Дифференциальные уравнения, описывающие поведение линейных систем, можно записать следующим образом:
dx /dt = Аx + b, (1)
где x – вектор переменных состояния, чаще всего это концентрация вещества или температура; А – матрица коэффициентов, которая характеризует выходные потоки вещества или энергии ХТС; b – вектор, характеризующий входные потоки веществ или энергии; t – время.
Всегда существует система ограничений по переменным состояния, выделяющая тот или иной режим работы ХТС, следующего вида:
xik(min) < xi < xik(мах), (i=1,I; k=1,Ki) (2)
или в векторной форме: xk(min) < x < xk(мах),
где i – номер переменной состояния; k – номер технологического режима работы i-й переменной.
Наличие таких технологических ограничений на переменные состояния позволяет с какой угодно степенью дифференциации перечислять на основе чисто комбинаторного перебора возможные непересекаемые области существования переменных состояния или, как это было определено в [1-3], элементы алфавита состояний ai, которые характеризуют конкретные технологические режимы работы ХТС.
На основе неравенств (2) и системы (1) можно получить системы линейных ограничений (3), (4) для статических и системы (5), (6) для квазистатических режимов работы, выделяющие области элементов матрицы А и вектора b, соотносящиеся с некоторой областью состояний (2). Естественно, при этом необходимо учитывать систему ограничений (7), (8):
Xq< z < 0, (3)
Xq> z > 0, (4)
(Xiq<(k), z(k)) < Dx(k+1), (i =1,...,I), (5)
(Xiq>(k), z(k)) > Dx(k+1), (i =1,...,I), (6)
aij(min)
bi(min) < bi < bi(мах), (i=1, 2, …, I), (8)
где Xq<, Xq> – матрицы Xq, образованные нижней и верхней границами для q-го режима работы по координатам переменных состояния x на основе ограничений (2).
Задача состоит в том, чтобы при заданных x(min) и x(мах) найти диапазоны изменения коэффициентов системы aij(min) и aij(мах) (i=1,I; j=1,I), а также bi(min) и bi(мах) (i=1,I) таким образом, чтобы была справедлива система ограничений (3) и (4).
Здесь следует отметить, что подобного рода задачи часто встречаются при моделировании реальных систем. Как правило, известны лишь диапазоны изменения переменных состояния x. В этом случае очень важно определить связь между текущими значениями переменных состояния и значениями, показываемыми контрольно-измерительным оборудованием. Эта связь может быть задана матрицей A, коэффициенты которой изменяются в некотором неизвестном диапазоне.
Предлагаемый метод решения осуществляет поиск ограничений перебором с переменным шагом. Для этого мы задаем начальное положение системы и определяем минимальное значение шага. Поиск проходит в два этапа: сначала ищется матрица максимальных значений коэффициентов, а затем минимальных.
Рассмотрим алгоритм поиска минимальных значений, а максимальные значения ищутся аналогично.
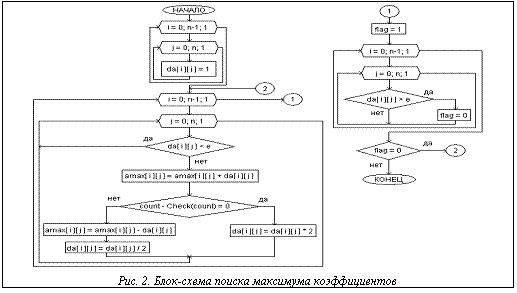
 Матрице A(min) присваивается начальное значение, определяемое заданными коэффициентами. Затем идет последовательное изменение (уменьшение) каждого коэффициента на величину шага, определяемую соответствующим значением матрицы шагов dA (для каждого коэффициента системы рассчитывается свой шаг, что существенно повышает эффективность алгоритма). После изменения каждого коэффициента делается проверка, не вышло ли решение (3) за пределы искомого диапазона. Если проверка не дала положительного результата, выполняется возврат, коэффициенту присваивается исходное значение. Далее вычисляется новый шаг для текущего коэффициента – увеличение вдвое, если проверка была пройдена успешно, или уменьшение вдвое в противном случае. Новое значение шага записывается в матрицу dA. Если шаг оказался меньше заданного минимального значения, текущий коэффициент более не меняется.
Матрице A(min) присваивается начальное значение, определяемое заданными коэффициентами. Затем идет последовательное изменение (уменьшение) каждого коэффициента на величину шага, определяемую соответствующим значением матрицы шагов dA (для каждого коэффициента системы рассчитывается свой шаг, что существенно повышает эффективность алгоритма). После изменения каждого коэффициента делается проверка, не вышло ли решение (3) за пределы искомого диапазона. Если проверка не дала положительного результата, выполняется возврат, коэффициенту присваивается исходное значение. Далее вычисляется новый шаг для текущего коэффициента – увеличение вдвое, если проверка была пройдена успешно, или уменьшение вдвое в противном случае. Новое значение шага записывается в матрицу dA. Если шаг оказался меньше заданного минимального значения, текущий коэффициент более не меняется.
После того как будет сделан проход по всей матрице A(min), программа анализирует матрицу шагов и смотрит, остались ли элементы, не достигшие предела. Если таковые найдены, процесс повторяется и для них. Если же все элементы достигли предела, программа переходит к следующему этапу.
 Проверка на принадлежность решения Аx+b= =0 диапазону (2) коэффициентов матрицы A и вектора b, рассчитанных на очередной итерации, производится следующим образом.
Проверка на принадлежность решения Аx+b= =0 диапазону (2) коэффициентов матрицы A и вектора b, рассчитанных на очередной итерации, производится следующим образом.
Большое количество раз случайным образом генерируется система коэффициентов матрицы A и вектора b из текущего диапазона. Если в каждом случае решения системы выполняются ограничения (3) и (4), проверка считается удачно пройденной. Если же хотя бы при одной из попыток был выход решений за допустимый диапазон, проверка завершается неудачно. При достаточно большом количестве испытаний надежность составляет 95% – 97%, что во многих случаях достаточно для практических расчетов.
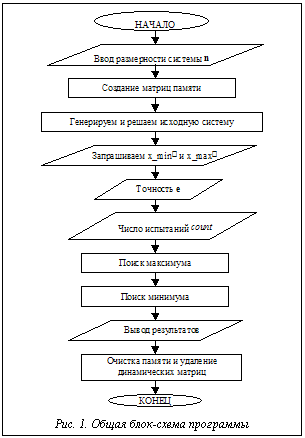
Приведенный выше метод решения может быть записан в виде следующего алгоритма.
1. Увеличиваем (при поиске минимума уменьшаем) значение очередного коэффициента на соответствующее значение из матрицы dA.
2. Делаем статистическую проверку в функции check().
3. Если проверка завершилась неудачно, возвращаем коэффициенту исходное значение, а соответствующий элемент из матрицы dA уменьшаем вдвое.
4. Если же проверка прошла успешно, увеличиваем шаг изменения (элемент матрицы dA) вдвое.
5. Если значение соответствующего элемента матрицы dA стало меньше, чем заданный предел точности, считаем, что граница изменения данного коэффициента системы достигнута, и в дальнейшем пропускаем этот коэффициент.
6. Переходим к следующему коэффициенту.
7. Как только все коэффициенты достигли предельных значений, переходим к следующему этапу.
 Реализация алгоритма была проведена на примере дискретных моделей производства слабой азотной кислоты (САК).
Реализация алгоритма была проведена на примере дискретных моделей производства слабой азотной кислоты (САК).
Анализ технологической схемы производства САК как объекта технической диагностики позволил выделить три реакторных узла для построения дискретных моделей: узел подготовки аммиачно-воздушной смеси и окисления аммиака, включающий в себя смеситель с фильтром и контактный аппарат, узел получения азотной кислоты – абсорбционная колонна и узел каталитической очистки хвостовых газов.
Основные уравнения материальных и тепловых балансов и основные ограничения дискретной модели представлены в таблице.
Проверка работоспособности алгоритма показала, что диапазоны основных параметров для нормальных режимов работы производства САК могут изменяться в пределах 10-15 % от рабочей точки процесса.
Список литературы
1. Богатиков В.Н., Борисов А.Л. Построение дискрет- ных моделей диагностики химических производств // Меж- дунар. конф.: "Математические методы в химии и химической технологии" (ММХ-9): Сб. тез. Ч. 4.- Тверь, 1995.- С. 145.
2. Богатиков В.Н., Палюх Б.В. Построение дискретных моделей химико-технологических систем. Теория и практика. - Апатиты, 1995. - 162 с.
3. Богатиков В.Н., Гордеев Л.С., Егоров А.Ф., Савиц- кая Т.В. Методология управления технологической безопасностью непрерывных химико-технологических процессов. “Управление безопасностью природно-промышленных систем”. Вып. 2. / Под ред. В.А. Путилова. -М.: Изд-во КНЦ РАН. - 1999. - С. 16-42.



 Матрице A(min) присваивается начальное значение, определяемое заданными коэффициентами. Затем идет последовательное изменение (уменьшение) каждого коэффициента на величину шага, определяемую соответствующим значением матрицы шагов dA (для каждого коэффициента системы рассчитывается свой шаг, что существенно повышает эффективность алгоритма). После изменения каждого коэффициента делается проверка, не вышло ли решение (3) за пределы искомого диапазона. Если проверка не дала положительного результата, выполняется возврат, коэффициенту присваивается исходное значение. Далее вычисляется новый шаг для текущего коэффициента – увеличение вдвое, если проверка была пройдена успешно, или уменьшение вдвое в противном случае. Новое значение шага записывается в матрицу dA. Если шаг оказался меньше заданного минимального значения, текущий коэффициент более не меняется.
Матрице A(min) присваивается начальное значение, определяемое заданными коэффициентами. Затем идет последовательное изменение (уменьшение) каждого коэффициента на величину шага, определяемую соответствующим значением матрицы шагов dA (для каждого коэффициента системы рассчитывается свой шаг, что существенно повышает эффективность алгоритма). После изменения каждого коэффициента делается проверка, не вышло ли решение (3) за пределы искомого диапазона. Если проверка не дала положительного результата, выполняется возврат, коэффициенту присваивается исходное значение. Далее вычисляется новый шаг для текущего коэффициента – увеличение вдвое, если проверка была пройдена успешно, или уменьшение вдвое в противном случае. Новое значение шага записывается в матрицу dA. Если шаг оказался меньше заданного минимального значения, текущий коэффициент более не меняется. Проверка на принадлежность решения Аx+b= =0 диапазону (2) коэффициентов матрицы A и вектора b, рассчитанных на очередной итерации, производится следующим образом.
Проверка на принадлежность решения Аx+b= =0 диапазону (2) коэффициентов матрицы A и вектора b, рассчитанных на очередной итерации, производится следующим образом.
