Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Поиск во временном ряде фрагментов, «похожих» на заданный шаблон
Аннотация:
Abstract:
| Авторы: Прохоров А.Ю. () - , Сотников А.Н. (asotnikov@iscc.ru) - Федеральный исследовательский центр «Информатика и управление» РАН, ул. Вавилова, 44-2, г. Москва, 119333, Россия (главный научный сотрудник), г. Москва, Россия, доктор физико-математических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15354 |
Версия для печати Выпуск в формате PDF (13.63Мб) |
Во всех приведенных примерах в наблюдаемой характеристике ищется временной интервал, когда она ведет себя определенным образом. Потребность в решении данной задачи существует и нуждается в строгой математической формулировке, в рассмотрении методов решения и их оптимизации. Построенная алгебраическая модель информационного поиска [1], в том числе и с использованием различных мер сходства [2,3], в рамках которой процесс поиска сводился к задаче решения системы линейных алгебраических уравнений в конечномерном векторном пространстве, дала четкое понимание процесса поиска, позволила ставить и решать задачи его оптимизации, в том числе с учетом особенностей предметной области. Временной ряд. Основные определения
Определение 1. Временной ряд представляет собой совокупность величин вида: Здесь Одним из признаков, по которым классифицируют временные ряды, является количество наблюдаемых характеристик. Определение 2. Временной ряд называется одномерным, если он получен в результате наблюдения одной характеристики: Определение 3. Временной ряд называется многомерным, если он получен в результате наблюдения более одной характеристики В самом общем виде временной ряд представляет собой матрицу, изображенную на рисунке 1. Как видно, важной особенностью многомер- ного временного ряда является то, что значения всех характеристик измеряются в один момент времени Определение 4. Временной ряд Регулярные ряды являются наиболее удобными для исследования. Для них разработан широкий спектр методов анализа. При этом регулярный одномерный временной ряд часто представляют в виде вектора значений, заменяя фактическое время наблюдения целочисленным индексом. Такой объект является очень удобным для описания математических операций. Сравнение временных рядов В последние годы возник принципиально новый тип задач в самых различных прикладных областях. Суть проблемы заключается в поиске во временном ряде фрагментов, в которых наблюдаемая характеристика ведет себя определенным образом. Пока в большинстве работ [5-7] данная задача формулируется для определенного подмножества временных рядов. Фактически исследуются только одномерные, регулярные временные ряды. При этом ряд представляется в виде вектора действительных величин. Обычно то, как должна вести себя наблюдаемая характеристика, определяется заданием вектора Определение 5. Шаблон Следующее утверждение определяет трудоемкость поиска во временном ряде. Теорема 1. Для поиска во временном ряде длины Для исследования наибольший интерес представляют временные ряды, порожденные стохастическими по своей природе признаками. Для таких рядов нельзя в точности вычислить значение характеристики как значение некоторой неслучайной функции времени Если временной ряд является детерминированным, то значение его характеристик можно однозначным образом описать в виде некоторых функций времени Таким образом, в реальных задачах не приходится ожидать точного совпадения шаблона с фрагментом ряда. Кроме того, очень часто при наблюдении процесса вкрадываются неизбежные ошибки дискретизации, связанные с преобразованием аналоговых величин в цифровое представление. Вследствие этого необходимо рассчитывать не на полное совпадение, а на приблизительное, с заданной точностью. Понятие примерная схожесть легко воспринимается человеком визуально, при этом гораздо сложнее выражается формальными методами. В работе [5] были предложены формальные методы определения похожести (similarity) временных рядов. Авторы ввели два понятия: похожесть и примерная похожесть временных рядов. Пусть на множестве одномерных временных рядов Определение 6. Временные ряды Теорема 2. Для любых одномерных временных рядов Очевидно, что практическую ценность определение 6 будет иметь только при конкретном определении метода преобразования. Поэтому далее как T будет обозначаться конкретное преобразование. Теперь можно перейти к определению примерной схожести временных рядов. Для этого необходимо ввести оценку несоответствия временных рядов. Оценить такое несоответствие можно по расстоянию между рядами. Понятие расстояния вводится как некоторая мера D, определенная на пространстве векторов Определение 7. Одномерные временные ряды Авторы [5] предложили ограничиться линейным преобразованием T элементов ряда. Определение 8. Линейным преобразованием Видно, что для прямого преобразования Действительно, Линейное преобразование удобно использовать для приведения временных рядов к некоторому общему виду. Чтобы определить такой общий вид временного ряда, определим понятие среднего значения и дисперсии. Пусть среднее значение вычисляется как Определение 9. Одномерный временной ряд X называется нормальным, если среднее значение равно 0, а дисперсия 1 либо 0. В определении специально оговорен случай, когда дисперсия равна 0 для сохранения общности рассуждений. Теорема 3. Любой одномерный временной ряд с дисперсией, отличной от нуля, можно привести к нормальному ряду с помощью преобразования: Если дисперсия равна нулю, то ряд приводится к нормальному с помощью преобразования: Используя данную теорему, можно ввести определение похожести рядов для линейных преобразований. Определение 10. Одномерные временные ряды X и Y являются «похожими», если Таким образом, примерную схожесть рядов можно оценивать по расстоянию между нормальными формами рядов Чаще всего в качестве меры расстояния между рядами используется евклидово расстояние, которое определяется как: Теперь имеются все средства для определения степени схожести временных рядов, которое можно использовать в практических задачах. Определение 11. Одномерные временные ряды X и Y являются примерно похожими с точностью e Введенные понятия позволяют оперировать временными рядами, оценивать расстояние между ними. Однако прямое применение данных методов требует использования перебора для поиска фрагментов во временном ряде, похожих на заданный шаблон. Теорема показывает, что поиск перебором всех фрагментов ряда требует большого объема вычислений. Таким образом, необходимо искать методы оптимизации поиска применительно к поставленной задаче. Оптимизация поиска В работах [1-3] был предложен обобщенный алгоритм поиска в линейном многомерном пространстве, основанный на алгоритмах отсечения, позволяющий при достаточно простых средствах организации поискового пространства ограничить поиск в нем, исключив из него подмножества заведомо не содержащие элементы искомого множества решений. Подобные принципы применяются при построении R-tree [8] индексов, которые широко используются для поиска многомерных структур данных. Применение индексов для задач поиска фрагментов ряда Как показано выше, прямое решение задачи поиска фрагментов ряда, похожих на заданный шаблон, является крайне трудоемким. Так, при длине исходного ряда N и ширине шаблона n требуется порядка Большая часть предлагаемых в настоящий момент способов индексирования, применяемых для решения данной задачи, объединяется одной общей идеей. Суть ее заключается в том, что к шаблону Для вычисления расстояния между исходными временными рядами по образам фрагмента и шаблона необходимо, чтобы преобразование T сохраняло расстояние между рядами: Таким образом, для построения индекса следует подобрать преобразование T, которое бы сохраняло расстояние между рядами и существенно уменьшало бы длину их образов. Такая общая постановка задачи может быть несколько упрощена. Дело в том, что в конкретных прикладных областях очень часто используется весьма ограниченный набор норм для оценки расстояния. Кроме того, временные ряды, типичные для одной прикладной области, обычно обладают общим набором свойств. При этом в рамках конкретной прикладной области может быть задана норма для вычисления расстояния D. На практике для заданного множества временных рядов очень редко удается подобрать такое преобразование, которое бы существенно сокращало длину рядов, и при этом сохраняло расстояние между ними. Обычно удается достичь незначительного уменьшения расстояния между образами:
Таким образом, индекс будет представлять собой множество фрагментов
Здесь Y – заданный шаблон, а e – точность соответствия фрагмента шаблону. При поиске по такому индексу необходимо получить образ шаблона на основе такого же преобразования
Теорема 4. Если имеет силу условие (1), то все фрагменты Данная теорема гарантирует, что при поиске по индексу будут найдены все искомые фрагменты Оценим выигрыш в производительности
Соотношение (4) подтверждает интуитивное предположение о том, что эффективность индекса зависит от сокращения длины ряда Следует отметить, что существуют резервы для дальнейшего повышения производительности при Использование пространственного индекса существенно сокращает количество операций, необходимых для ведения поиска по образам фрагментов. Их будет значительно меньше, чем
В результате при использовании пространственных индексов для поиска по образам фрагментов эффективность алгоритма в целом будет обратно пропорциональна селективности запроса. Методика оценки эффективности индекса при поиске фрагментов временного ряда Методика проверки эффективности необходима еще на этапе проектирования нового типа индекса. Она должна показать целесообразность применения данного типа индекса и по возможности определить условия, при которых данный метод индексирования позволяет добиться наилучших результатов. Проверка может проводиться аналитическим либо экспериментальным путем. Каждый из этих путей имеет свои достоинства и недостатки. Экспериментальный путь, с одной стороны, позволяет фактически подтвердить целесообразность использования конкретной методики. С другой стороны, он требует практической реализации индекса, что является достаточно трудоемким процессом. При этом качество реализации индекса может вносить свои погрешности, приводящие к ухудшению экспериментальных показателей. Аналитический способ проверки позволяет получить оценки эффективности, не прибегая к трудоемким практическим экспериментам. Соответственно, недостатком данного способа является то, что он не позволяет получить практического подтверждения теоретическим предположениям. Очевидно, что наиболее совершенная методика должна опираться на оба метода оценки. Изначально должны проводиться аналитические оценки, которые затем подтверждаются практическими результатами. В исследовательских работах, в которых предлагаются новые методы построения индексов для ускорения поиска по временному ряду, делаются попытки проведения как аналитической, так и практической проверки новых методов. Однако в аналитических оценках используются различные подходы. Оборудование, на котором проводятся экспериментальные оценки, также зависит от обеспечения конкретной университетской лаборатории. Таким образом, в настоящий момент сравнение различных методик построения индексов представляется затруднительным. На первом этапе необходимо, по крайней мере, определить общую методику аналитической оценки эффективности метода индексирования. В качестве такой методики можно использовать построение характеристической функции. Определение 12. Пусть заданы некоторое множество фрагментов Теорема 5. Характеристическая функция t(e) является неубывающей. Данная теорема и само определение характеристической функции позволяют описать основные свойства характеристической функции. Общий вид графика этой функции изображен на рисунке 2. Следствие 1. Характеристическая функция имеет максимум, равный количеству фрагментов N. Максимум достигается при e=emax – максимальном расстоянии между шаблоном и фрагментами ряда. Аналогичным способом строится характеристическая функция для образов фрагментов ряда и шаблона. Для нее также будет справедлива теорема 5, так как ее выводы не зависят от природы шаблона и фрагментов. Теорема 6. Если используемое для получения образов фрагментов ряда и шаблона преобра- зование T удовлетворяет условию (1): Таким образом, характеристические функции для исходных рядов и их образов имеют вид, изображенный на рисунке 3. Такой график позволяет оценивать эффективность индекса, построенного на основе заданного преобразования T.
Кроме того, характеристические функции образов могли бы быть использованы оптимизатором СУБД, использующей такие индексы. При помощи характеристических функций оптимизатор может принимать решения о необходимости использования индекса при заданном e1, а также о его выборе, если индексов несколько. Однако в исходном виде характеристическая функция строится только для одного заданного шаблона. Естественно предположить, что для поиска по фрагментам ряда будут использоваться шаблоны той же природы со схожими характеристиками, что и исходный временной ряд. Поэтому оптимизатором запросов может быть использована несколько видоизмененная характеристическая функция. Определение 13. Пусть задано некоторое множество фрагментов Соответствующее множество расстояний между фрагментами можно представить в виде матрицы, изображенной на рисунке 4. Диагональные элементы этой матрицы равны 0, так как являются расстоянием между одним и тем же фрагментом. Кроме того, матрица симметрична, так как мера расстояния также должна быть симметричной, то есть
Данный подход позволит при построении различных типов индексов по одному и тому же ряду в зависимости от параметров запроса выбирать тот тип индекса, который обеспечит лучшую производительность. В заключение отметим, что задаче поиска во временном ряде фрагмента, похожего на заданный шаблон, дана строгая математическая формулировка. Рассмотрены методы оптимального решения этой задачи при помощи построения индексов. Для сравнения различных типов индексов предложена характеристическая функция. При этом предложена модификация характеристической функции, которая может быть использована оптимизатором СУБД для выбора оптимального метода выполнения запроса при практической реализации индексов. Список литературы 1. Решетников В.Н. Информационный поиск и z-струк-тура. [Сборник]: Математические вопросы задач оптимизации и управления. - М.: Изд-во МГУ, 1981. 2. Сотников А.Н. Псевдорелевантные векторы и их свойства. [Сборник]: Математические вопросы задач оптимизации и управления. - М.: Изд-во МГУ, 1981. 3. Сотников А.Н., Трофимова Е.Г. О некоторых свойствах мер сходства в задаче информационного поиска. // Сб. тр. ВМК МГУ: Системное программирование и вопросы оптимизации. - М.: Изд-во МГУ, 1987. 4. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. - М.: Юнити, 1998. 5. Goldin D.Q., Kanellakis P.C. On Similarity Queries for Time-Series Data: Constraint Specification and Implementation. In 1st International Conference on the Principles and Practice of Constraint Programming, pp. 137-153, 1995. 6. Faloutsos C., Ranganathan M., Manolopoulos Y. Fast Subsequence Matching in Time-Series Databases. In Proc. of the ACM SIGMOD Conference on Management of Data, 1994. 7. Rafiei D., Mendelzon A. Similarity-Based Queries for Time Series Data. in Proc. of the ACM SIGMOD Conference on Management of Data, 1997. 8. Guttman A. R-trees: a Dynamic Index Structure for Spatial Searching. In Proceeding ACM SIGMOD International Conference on Management of Data, Boston, MA, 1984, pp. 47-57. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=623&page=article |
Версия для печати Выпуск в формате PDF (13.63Мб) |
| Статья опубликована в выпуске журнала № 3 за 2003 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Новый подход к проблеме коллективного выбора на базе удовлетворения взаимных требований сторон
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам
- Системы баз данных и знаний, разработанные в Республике Куба
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- К вопросу параметризации свойств программных средств обучения
Назад, к списку статей



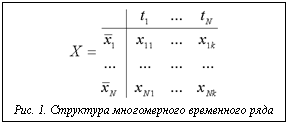 Математическим объектом, с помощью которого описывается наблюдаемая с течением времени характеристика, является временной ряд. С содержательной точки зрения временной ряд представляет собой «расположенную в хронологическом порядке последовательность наблюденных значений какого-либо признака» [4]. Это самое общее определение временного ряда. Ниже оно приводится в формальном виде.
Математическим объектом, с помощью которого описывается наблюдаемая с течением времени характеристика, является временной ряд. С содержательной точки зрения временной ряд представляет собой «расположенную в хронологическом порядке последовательность наблюденных значений какого-либо признака» [4]. Это самое общее определение временного ряда. Ниже оно приводится в формальном виде.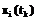
 ,
,  .
.
 – момент проведения измерения,
– момент проведения измерения,  – наблюдаемая характеристика
– наблюдаемая характеристика  [4].
[4]. ,
,  ,
,  . При этом каждый вектор
. При этом каждый вектор  можно рассматривать как одномерный временной ряд.
можно рассматривать как одномерный временной ряд. .
. ряда
ряда  ,
,  , если
, если  .
.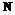 всех фрагментов, похожих на шаблон длины n, методом перебора необходимо
всех фрагментов, похожих на шаблон длины n, методом перебора необходимо  операций сравнения.
операций сравнения. . Эти ряды являются недетерминированными.
. Эти ряды являются недетерминированными. . В результате известен закон, по которому изменяются значения наблюдаемых характеристик, и величину этих характеристик можно точно предсказать для любого момента времени. Поэтому для детерминированных временных рядов задачи анализа и прогнозирования значений становятся вырожденными.
. В результате известен закон, по которому изменяются значения наблюдаемых характеристик, и величину этих характеристик можно точно предсказать для любого момента времени. Поэтому для детерминированных временных рядов задачи анализа и прогнозирования значений становятся вырожденными. задано некоторое множество допустимых преобразований
задано некоторое множество допустимых преобразований  , таких что
, таких что  .
. и
и  являются похожими, если они имеют одинаковую длину и существует такое преобразование
являются похожими, если они имеют одинаковую длину и существует такое преобразование 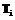 , что
, что  .
. и
и  одинаковой длины существует преобразование
одинаковой длины существует преобразование  .
. .
. являются примерно похожими с точностью e, если они имеют одинаковую длину и расстояние D между рядами удовлетворяет условию:
являются примерно похожими с точностью e, если они имеют одинаковую длину и расстояние D между рядами удовлетворяет условию:  e.
e. называется линейное преобразование вида:
называется линейное преобразование вида:  , где a>0 и
, где a>0 и  .
. существует обратное преобразование
существует обратное преобразование 
 .
.
 .
. , а дисперсия
, а дисперсия  .
. .
. .
. .
. .
. .
. , если
, если  e.
e. операций. Очевидна необходимость поиска путей, которые позволили бы сократить количество вычислительных операций. Одним из таких путей является построение индекса по исходному временному ряду, который мог бы ускорить выполнение задачи.
операций. Очевидна необходимость поиска путей, которые позволили бы сократить количество вычислительных операций. Одним из таких путей является построение индекса по исходному временному ряду, который мог бы ускорить выполнение задачи. и всем фрагментам временного ряда
и всем фрагментам временного ряда  применяется некоторое преобразование
применяется некоторое преобразование  . Получаемые в результате этого преобразования векторы
. Получаемые в результате этого преобразования векторы  имеют меньшую длину
имеют меньшую длину  , где
, где  . Это же преобразование применяется и к шаблону
. Это же преобразование применяется и к шаблону  . Теперь для сравнения образов понадобится существенно меньше операций. Выигрыш будет пропорционален уменьшению длины образов по сравнению с длиной исходных векторов
. Теперь для сравнения образов понадобится существенно меньше операций. Выигрыш будет пропорционален уменьшению длины образов по сравнению с длиной исходных векторов  .
.
 .
. . (1)
. (1) ,
,  , где
, где  . Такой индекс может быть использован для ускорения поиска фрагментов
. Такой индекс может быть использован для ускорения поиска фрагментов  , где
, где  и
и  , удовлетворяющих условию:
, удовлетворяющих условию: e. (2)
e. (2) . В индексе будут искаться образы, удовлетворяющие условию:
. В индексе будут искаться образы, удовлетворяющие условию: e . (3)
e . (3) , получаемый при использовании описанного выше индекса. Для этого сравним количество операций, которые необходимо выполнить при последовательном переборе и при поиске по индексу. Обозначим количество выбираемых образов как k, тогда:
, получаемый при использовании описанного выше индекса. Для этого сравним количество операций, которые необходимо выполнить при последовательном переборе и при поиске по индексу. Обозначим количество выбираемых образов как k, тогда: , при
, при 
 . (4)
. (4) в результате используемого преобразования T и от селективности
в результате используемого преобразования T и от селективности  выборки образов фрагментов временного ряда. При этом следует учесть, что селективность выборки образов, в свою очередь, зависит от нескольких параметров. С одной стороны, это заданные шаблон Y и точность e, с другой стороны, это множество фрагментов ряда
выборки образов фрагментов временного ряда. При этом следует учесть, что селективность выборки образов, в свою очередь, зависит от нескольких параметров. С одной стороны, это заданные шаблон Y и точность e, с другой стороны, это множество фрагментов ряда  ~ 1. В этом случае при поиске по образам фрагментов может быть использован пространственный индекс, например типа R-tree [8], который позволит избежать последовательного перебора. При
~ 1. В этом случае при поиске по образам фрагментов может быть использован пространственный индекс, например типа R-tree [8], который позволит избежать последовательного перебора. При  . Поэтому эту составляющую можно будет отбросить при оценке эффективности механизма индексированного поиска в целом:
. Поэтому эту составляющую можно будет отбросить при оценке эффективности механизма индексированного поиска в целом: . (5)
. (5) временного ряда, шаблон Y и мера D сравнения шаблона и фрагментов. Тогда характеристическая функция t(e) определяется как количество фрагментов n, для которых расстояние между ними и шаблоном меньше либо равно заданной точности e, то есть t(e)
временного ряда, шаблон Y и мера D сравнения шаблона и фрагментов. Тогда характеристическая функция t(e) определяется как количество фрагментов n, для которых расстояние между ними и шаблоном меньше либо равно заданной точности e, то есть t(e) , где
, где  :
:  .
. для всех образов фрагментов ряда
для всех образов фрагментов ряда  и шаблона
и шаблона  :
:  , где t(e) – характеристическая функция, а
, где t(e) – характеристическая функция, а  – характеристическая функция образов.
– характеристическая функция образов.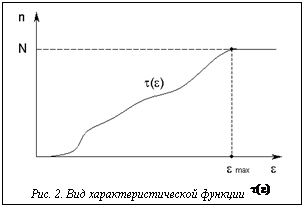 Как было показано ранее, эффективность индекса зависит от селективности выборки
Как было показано ранее, эффективность индекса зависит от селективности выборки  , при использовании индекса. Чем меньше оказывается
, при использовании индекса. Чем меньше оказывается 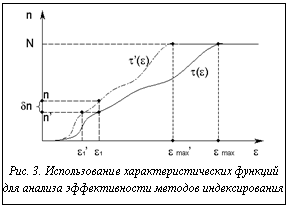 За счет построения на одном графике характеристических функций для образов, полученных в результате применения различных преобразований, можно наглядно сравнивать их применимость для заданных фрагментов и шаблона. Такой график может служить простым и доступным средством сравнения различных методик построения индексов.
За счет построения на одном графике характеристических функций для образов, полученных в результате применения различных преобразований, можно наглядно сравнивать их применимость для заданных фрагментов и шаблона. Такой график может служить простым и доступным средством сравнения различных методик построения индексов. , где
, где  :
:  e.
e.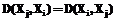 .
. Поэтому информативными являются половина отличных от нуля элементов
Поэтому информативными являются половина отличных от нуля элементов  . Для них и имеет смысл строить автохарактеристическую функцию, которая будет иметь такой же вид, как и характеристическая функция. С помощью автохарактеристической функции можно оценивать селективность запроса по заданному e. Конечно, такая функция не будет давать точного значения селективности запроса, однако даже приблизительная оценка будет полезна для оптимизатора запросов.
. Для них и имеет смысл строить автохарактеристическую функцию, которая будет иметь такой же вид, как и характеристическая функция. С помощью автохарактеристической функции можно оценивать селективность запроса по заданному e. Конечно, такая функция не будет давать точного значения селективности запроса, однако даже приблизительная оценка будет полезна для оптимизатора запросов.