Исследование многокритериальной задачи информационного поиска в рамках линейной алгебраической модели
| Терехин А.Н. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Исследование различных задач информационного поиска удобно проводить в рамках линейной алгебраической модели [1-3], где поисковые образы документов и запросов представляются элементами конечномерного векторного пространства, а поиск сводится к решению поискового уравнения, определяемого запросом, на конечном множестве. Рассматриваемый подход, как и большинство моделей поиска [4], отражает в большей степени попытку связать между собой представления документов в хранилищах данных и информационных запросов, нежели имитирует реальные процессы, в действительности происходящие при поиске. Характер этой связи описывается таким понятием, как релевантность, которое в данной модели интерпретируется путем введения мер близости между векторами. В работе рассматривается многокритериальная задача информационного поиска, описанная в рамках указанной модели, обсуждаются некоторые подходы к ее решению. Рассмотрим многокритериальную задачу:
где каждая задача r рассматривается на конечном множестве
а через G – совокупность симметрик rs: G={rs Класс G достаточно широк и применим на практике [5]. Приведем несколько примеров: – мера близости Минковского r1(x,y)= – мера близости Расела-Рао r2(x,y)=( – мера близости Танимото-Роджерса r3(x,y)= – геометрическая мера близости r4(x,y)= Если для решения задачи (1) использовать способы сведения к однокритериальной задаче (к примеру, путем линейной свертки), то она фактически сведется к задаче (2). Построение множества Введем в рассмотрение следующие понятия. Определение. Любые два вектора t', t" Неравенства вида
при этом отметим, что R={ Утверждение 1. Справедливо следующее вложение: Доказательство. Пусть Следствие 1. Справедливо вложение
Подмножества R и P, которые представляют собой псевдорелевантное и релевантное подмножества векторов соответственно, являются своего рода первым приближением множеств Следствие 2. Если Определим далее для Утверждение 2. Если Доказательство следует из построения векторов Следствие 1. Если приведенное утверждение выполнено для всех с= Следствие 2. Если Следствие 3. Алгоритм расширения подмножества 1. Построить подмножество
2. Определить подмножество
3. Если все 4. Построить множество
5. Для каждого
6. Для каждого
где 7. Стоп. Заметим, что построение подмножества R по причинам, приведенным выше, может вызвать затруднение. В этом случае следует положить Подытожим полученные результаты. Метод построения множества Конечно, такое дополнение следует проводить в том случае, если полученных решений явно недостаточно. В частности, по приведенной методике можно получать и точные решения поискового уравнения (все сделанные постро- ения и алгоритм поиска универсальны для определения как точных, так и приближенных решений). Утверждение 3. Задачу (1) можно свести к задаче вида
для нахождения хотя бы одного решения в случае использования метода линейной свертки при сведении задачи (1) к однокритериальной задаче. Задачу (1) можно решать методом введения метрики в пространстве целевых функций. Покажем, как, учитывая приведенные выше рассуждения, можно эффективно использовать этот метод для построения хотя бы одного решения задачи (3) – множества Утверждение 4. Пусть для каждого s определены различные
где Чтобы найти все решения задачи (3), следует получить решения каждой из задач минимизации, используя алгоритм расширения, а далее решать задачу (4) на Для нахождения всех решений рассматриваемой задачи (1) можно использовать идею алгоритма отсечения [6-8]. Представим множество T в виде
Введем следующие обозначения: I={1, …, c, …, p},
Утверждение 5. Пусть подмножества Тогда, если Доказательство.
и соответственно
Тогда по условию справедливы следующие неравенства:
Пусть
С учетом определения (2) утверждение доказано. Утверждение 6. Пусть Тогда Доказательство. Пусть r Утверждение доказано. Следствие. Алгоритм отсечения для зада- чи (2). 1. Вычислить значения 2. Упорядочить 3. Определить множества индексов J:
4. Если 5. Определить множество индексов 6. Вычислить 7. Определить множество индексов 8. Перейти к п. 4. 9. Стоп. Понятно, что в случае сведения задачи (1) к однокритериальной целесообразно использовать приведенные выше утверждения для оптимизации ее решения [9]. Рассмотрим в данном случае возможность эффективного использования метода введения метрики в пространстве целевых функций. Утверждение 7. Пусть для каждого s определим различные где Доказательство. Пусть Так как rs Далее очевидно, что Тогда Из изложенного выше видно, что использование алгоритма отсечения в данном случае может оказать двойную услугу: во-первых, при решении задач вида (3) и, во-вторых, как следствие, представляется возможность решать задачу минимизации критерия h на множестве меньшей мощности. Список литературы 1. Решетников В.Н. Алгебраическая теория информационного поиска. // Программирование. - 1979.- № 3. - C. 78-83. 2. Решетников В.Н. Моделирование информационного поиска в информационно-поисковых системах. // Кибернетика. - 1979. - №5. - C. 129-132. 3. Решетников В.Н. Алгебраические модели информационного поиска. // Математические методы в исследовании операций. -М.: Изд-во МГУ, 1981. - С.186-192. 4. Boyce B., Kraft D.H. Principles and theories in information science. // Annv.Rev.Inf.Sci.Tech.1985.20.P.153-178. 5. Лейбкинд А.Р., Рудник Б.В. Моделирование организационных структур. - М., 1981. 6. Сотников А.Н. Алгоритм отсечения для различных мер сходства в задаче информационного поиска. // Вестник Моск. ун-та. Сер.15: Вычисл. матем. и киберн. - 1986. - №1. - С.70-77. 7. Решетников В.Н., Сотников А.Н. Алгоритмы отсечения для построения псевдорелевантных множеств.//Программное обеспечение вычислительных комплексов. - М.: Изд-во МГУ, 1985. - С.60-64. 8. Терехин А.Н. О применимости алгоритма отсечения для решения задач многокритериального информационного поиска. // Вестник Моск. ун-та. Сер.15: Вычисл. матем. и киберн. - 1989. - №4.- С.57-62. 9. Терехин А.Н., Пшенко С.Ю. О решении многокритериальных задач информационного поиска на матричных архивах. // Программное обеспечение и модели системного анализа. - М.: Из-во МГУ, 1991.- С.19-26. 10. Cотников А.Н. Терехин А.Н. Методы исследования задач псевдорелевантного информационного поиска. // Вопросы кибернетики. Анализ больших систем. - М., 1992. - С. 166-178. |
http://swsys.ru/index.php?id=625&lang=%29&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Система поддержки принятия решений по планированию профессиональной структуры подготовки специалистов
- Макроэкономическая балансовая модель для стран с элементами переходной экономики
- Зарубежные базы данных по программным средствам вычислительной техники
- Знания в интеллектуальных системах

 (1)
(1) (2)
(2) – векторов из линейного пространства
– векторов из линейного пространства  размерности m над полем коэффициентов
размерности m над полем коэффициентов  .
.  – оператор проекции на линейное пространство
– оператор проекции на линейное пространство  , порожденное вектором q [1-3]. В
, порожденное вектором q [1-3]. В 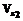 зафиксируем базис
зафиксируем базис  и рассмотрим некоторую совокупность функций r
и рассмотрим некоторую совокупность функций r . Данные функции характеризуют силу попарных связей между векторами из T, являются неотрицательными и симметричными. В литературе они получили название мер близости, или симметрик. Обозначим множество решений задачи (2) через
. Данные функции характеризуют силу попарных связей между векторами из T, являются неотрицательными и симметричными. В литературе они получили название мер близости, или симметрик. Обозначим множество решений задачи (2) через r
r , (3)
, (3)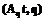 :
: ,
, ,
, , i=1,2, если
, i=1,2, если  , то rs
, то rs rs
rs }.
}. целое;
целое; );
); ;
; .
. при большой мощности множества Т и последующей отсюда необходимости полного перебора всех его элементов может оказаться весьма трудоемким процессом. Ниже рассматривается один подход для решения задачи (2) и, как следствие, задачи (1).
при большой мощности множества Т и последующей отсюда необходимости полного перебора всех его элементов может оказаться весьма трудоемким процессом. Ниже рассматривается один подход для решения задачи (2) и, как следствие, задачи (1). будем называть сравнимыми, если для всех i=
будем называть сравнимыми, если для всех i= справедливо: либо
справедливо: либо  , либо
, либо  , где l=dim
, где l=dim .
. и
и 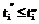 будем понимать в смысле приведенного определения.
будем понимать в смысле приведенного определения. Представим множество Т в виде Т= =
Представим множество Т в виде Т= = , при этом будем полагать, что все подмножества
, при этом будем полагать, что все подмножества  состоят из попарно сравнимых между собой векторов. Образуем совокупность верхних характеристических векторов:
состоят из попарно сравнимых между собой векторов. Образуем совокупность верхних характеристических векторов: =
= :
:  =
= ,
,
 =p, p
=p, p n. Обозначим через R множество
n. Обозначим через R множество
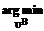 r(
r( .
. rs
rs , с=1, l, l
, с=1, l, l
 :
:  =
= , j=1,
, j=1,  , то (
, то ( )
) , а, следовательно,
, а, следовательно,  . Если таковых векторов нет, то
. Если таковых векторов нет, то 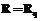 .
. , где
, где  ={
={ :rs
:rs  } и
} и rs
rs  .
. (
( ), то подмножество
), то подмножество  ).
). , где
, где  (операция
(операция  рассматривается в кольце целых чисел), с=
рассматривается в кольце целых чисел), с=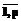 .
.
 ,
,  , с=1,l, l
, с=1,l, l } – индексы векторов базиса, соответствующие линейному подпространству
} – индексы векторов базиса, соответствующие линейному подпространству  .
. .
. , то
, то  .
. и
и  , то r – число векторов в соответствующем подмножестве
, то r – число векторов в соответствующем подмножестве  },
}, 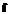
 p.
p. ={
={ }, где
}, где  =
= ,
, 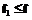 .
. , то
, то  и перейти к п. 7.
и перейти к п. 7.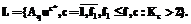
 определить
определить .
. , далее
, далее  ,
, .
. и повторить процедуру разбиения и необходимых построений.
и повторить процедуру разбиения и необходимых построений. rs
rs ,
, 

 .
. rs
rs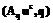 , (r*s=rs
, (r*s=rs ,
,  , тогда задачу (1) можно свести к задаче
, тогда задачу (1) можно свести к задаче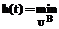 , (4)
, (4) (rs(Aquc,q)–r*s)2)1/2 – евклидово расстояние от точки r1(Aqt,q),…,rr(Aqt,q) до точки «абсолютного минимума» r*1,…,r*r в пространстве критериев.
(rs(Aquc,q)–r*s)2)1/2 – евклидово расстояние от точки r1(Aqt,q),…,rr(Aqt,q) до точки «абсолютного минимума» r*1,…,r*r в пространстве критериев.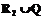 , где Q – объединение всех присоединенных векторов.
, где Q – объединение всех присоединенных векторов. ,
,  , при этом будем полагать, что подмножества
, при этом будем полагать, что подмножества  ,
,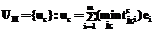 .
. r
r r
r .
. .
. , где подмножество индексов J=
, где подмножество индексов J= , то подмножества
, то подмножества  , не содержат решения задачи (3) (или псевдорешения уравнения (1)) в смысле рассматриваемой симметрики.
, не содержат решения задачи (3) (или псевдорешения уравнения (1)) в смысле рассматриваемой симметрики. , следуя (5), справедливы следующие неравенства:
, следуя (5), справедливы следующие неравенства:
 ,
,  .
. .
. . Очевидно, что
. Очевидно, что  . Тогда для
. Тогда для  справедлива следующая последовательность неравенств:
справедлива следующая последовательность неравенств: r
r r
r .
. , где
, где  r
r :r
:r ,
,  ,
,  .
. не содержит решения задачи (3).
не содержит решения задачи (3). ,
,  , тогда из условия следует, что
, тогда из условия следует, что  .
.  r
r .
. и
и  ,
,  .
. , то векторы подмножеств
, то векторы подмножеств  исключить из рассмотрения на принадлежность к множеству P, иначе перейти к п. 9.
исключить из рассмотрения на принадлежность к множеству P, иначе перейти к п. 9. .
. .
. , где
, где  r
r .
. rs
rs ,
,  и
и  – множества индексов тех
– множества индексов тех  :
:  , то задачу (1) можно свести к задаче
, то задачу (1) можно свести к задаче  ,
, – множества, не содержащие псевдорешений соответствующих задач из (4). Тогда
– множества, не содержащие псевдорешений соответствующих задач из (4). Тогда 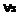 справедливо следующее неравенство: rs
справедливо следующее неравенство: rs rs
rs .
. , то (rs(Aqt,q)-r*s)2½tÎT\TK < (rs(Aqt,q)-r*s)2½tÎTK.
, то (rs(Aqt,q)-r*s)2½tÎT\TK < (rs(Aqt,q)-r*s)2½tÎTK.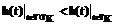 .
. , что и требовалось доказать.
, что и требовалось доказать.