Программы и модели для решения задач, связанных с подземными водами
| Каримов Р.Х. () - , Киселев А.А. () - , Копылов А.С. () - , Куранов П.Н. () - , Расторгуев А.В. () - , Хохлатов Э.М. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
На практике к подземным водам относятся двояко: 1) подземные воды являются ценным полезным ископаемым и нуждаются в экономном использовании и защите от загрязнения; 2) подземные воды вызывают подтопление территорий, оползневые явления и загрязняют поверхностные водотоки, для чего необходимы мероприятия по дренированию или перехвату загрязненного потока. В обоих утверждениях необходимо расчетное обоснование, которое в общем случае может быть выполнено на численных моделях. В статье дается описание программ и моделей для решения задач фильтрации и миграции подземных вод. Часть из них является разработкой авторов. В настоящее время наиболее применяемыми для решения практических задач, затрагивающих вопросы использования и защиты подземных вод, являются программа MODFLOW и ряд связанных с ней программ: MODPATH, MT3DMS, PEST и др. Разработка этого пакета программ начата более 20 лет назад, и в настоящее время он является наиболее оттестированным и надежным. MODFLOW и связанные с ней программы фактически являются мировым стандартом для решения проблем фильтрации и массопереноса. Большая часть задач, связанных с насыщенной однофазной фильтрацией в подземной гидросфере, решается на основе использования этих программ. В США пакет программ, связанных с MODFLOW, рекомендуется к использованию Агентством окружающей среды и Геологической службой. На сайтах этих организаций они могут быть получены вместе с тестовыми примерами, подтверждающими правильность результатов расчетов. В России MODFLOW и связанные с ней программы широко применимы, в том числе и в НИИ "ВОДГЕО". MODFLOW – программа Геологической службы США [12], реализующая блочно-центрированный балансовый метод конечных разностей (МКР) применительно к условиям нестационарного (в частном случае стационарного) трехмерного, неоднородного по фильтрационным свойствам потока. Первая версия программы, датируемая 1983 г., была написана на Фортране-66. Далее последовали ее редакции в 1996 и 2000 годах. С самого начала или, по крайней мере, с 1988 г. коды программы и ее описание стали открыты и распространялись бесплатно. MODFLOW имеет модульную структуру, то есть состоит из отдельных модулей, реализованных на языке Фортран в виде совокупности подпрограмм. При необходимости расширить возможности программы можно дописать дополнительный модуль. Открытые коды, описание и модульная структура позволили принять участие в тестировании и разработке MODFLOW многим специалистам. Программа MODFLOW обладает высоким быстродействием, которое достигается за счет использования современных быстродействующих методов решения систем разностных уравнений. По выбору вычислителя могут быть использованы как прямые, так и итерационные методы (метод сопряженных градиентов, неполной факторизации или верхней релаксации). В редакции 2000 г. в MODFLOW включен и многосеточный метод. В результате проведения численного моделирования трехмерной фильтрации с помощью MODFLOW удается получить файлы с напорами подземных вод в узловых точках, а также расходы потока между узлами. Расходы могут быть затем использованы для балансовых расчетов, моделирования конвективно-дисперсионного переноса и вычисления траекторий. MODPATH – программа для вычисления траекторий движения частиц [13]. Входной информацией для MODPATH являются скорости фильтрации подземных вод, полученные на основе расчетов с помощью MODFLOW, и координаты начальных точек. Далее из начальных точек можно произвести расчеты траекторий в направлении или против потока. Результаты расчетов выдаются в виде файла координат точек, составляющих траекторию. Опыт авторов по работе с MODPATH показывает, что это – полезная программа, позволяющая оценить зоны захвата водозаборных скважин, пространственную структуру потока подземных вод и многое другое. MT3DMS – программа позволяющая решать трехмерные задачи конвективно-дисперсионного массопереноса с учетом линейной и нелинейной сорбции, распада и двойной пористости [17]. Последняя версия программы, называемая MT3DMS, позволяет производить расчеты многокомпонентной миграции загрязняющих веществ без химических реакций между отдельными компонентами. Следует добавить, что MT3DMS основана на самых современных вычислительных алгоритмах, позволяющих решать задачи конвективно-дисперсионного переноса без численной дисперсии – это метод TVD и характеристик. PEST – программа для автоматизации калибровки моделей [9]. В большинстве случаев калибровку проводят методом проб-ошибок, при этом никогда нельзя быть уверенным в единственности полученных результатов. Программа PEST основана на методе нелинейной оптимизации, позволяющем найти набор параметров, соответствующих минимуму функции качества (сумма квадратов отклонений между модельными и фактическими данными). Личный опыт авторов по использованию PEST позволяет рекомендовать эту программу для решения практических задач. Все описанные выше программы написаны на языке Фортран. Данные для них готовятся в виде текстовых файлов, результаты расчетов также выводятся в текстовые файлы. Вполне реально готовить данные для моделей “вручную” с помощью текстовых редакторов, а результаты расчетов представлять с помощью графических пакетов или геоинформационных систем (ГИС). Однако при решении практических задач с большим количеством пространственно распределенных параметров удобно использовать специальные пакеты программ – пред- постпроцессоры. Пред- постпроцессоры обеспечивают удобную подготовку входных данных и визуализацию результатов расчетов. Применительно к описанному пакету программ в настоящее время разработаны несколько соизмеримых по возможностям пред- постпроцессоров: GMS [14], Groundwater Vistas [10], PMWIN [8], VISUAL MODFLOW [16]. Все эти программные средства содержат возможности для трехмерной визуализации результатов моделирования. Приведем пример использования пакета программ, связанных с MODFLOW, для обоснования защиты озера Байкал от загрязнения. В конце 80-х годов гидрогеологические исследования позволили установить факт загрязнения подземных вод в районе Байкальского целлюлозно-бумажного комбината (БЦБК). Загрязненный подземный поток разгружается в Байкал и ухудшает качество уникальной воды озера. С помощью численного моделирования были проведены расчеты перехватывающих скважин, позволяющих защитить Байкал от загрязнения подземными водами. Расчеты фильтрации подземных вод проводились в стационарной и нестационарной постановке на трехмерной численной модели. Моделируемая область была разбита неравномерной сеткой 100´75 блоков с размерами блоков от 240´200 м – в крайних частях модели, до 5´5 м – на участках расположения перехватывающих скважин. По вертикали моделируемая область была разбита на 6 слоев. Необходимость использования трехмерной модели связана с гидрогеологическими условиями в районе БЦБК. Моделирование трехмерной фильтрации было выполнено с помощью программы MODFLOW. Предварительно была проведена калибровка модели в процессе которой определяли коэффициент фильтрации, водоотдачу и техногенные утечки. Определение параметров осуществлялось с помощью программы PEST. Определенные в результате решения обратной задачи фильтрационные параметры были использованы для моделирования перехватывающих скважин. При расчетах защитных скважин определяли такое их размещение и производительность, чтобы обеспечить полный перехват загрязненных подземных вод, находящихся в ореоле. Степень перехвата оценивалась на основе расчета траекторий движения частиц, стартовое положение которых предварительно было задано на границе ореола. Пакет программ связанных с MODFLOW, направлен на решение задач фильтрации подземных вод и массопереноса для насыщенной области, расположенной ниже уровенной поверхности грунтовых вод. При оценке защищенности подземных вод возникает необходимость прогнозировать распространения загрязняющих веществ через зону неполного насыщения (зону аэрации), расположенную между поверхностью земли и уровнем грунтовых вод. Двухмерная фильтрация и миграция для областей полного и неполного насыщения может быть формализована в виде системы уравнений:
где
где
Насыщенность порового пространства водой определяется согласно
где Связь влагосодержания и давления осуществляется на основе уравнения состояния Ван Генухтена:
Компоненты тензора гидродинамической дисперсии в (3) определяются согласно
где Ниже приведено численное решение (1)-(3), выполненное применительно к прогнозу воздействия существующего полигона твердых бытовых отходов (свалки) на подземные воды. Модельные расчеты проводились с помощью программы SWMS_2D [15], позволяющей решать задачи насыщенной-ненасыщенной фильтрации и массопереноса методом конечных элементов Галеркина. Необходимые для моделирования фильтрационные параметры были взяты на основе лабораторных определений физико-механических свойств, базы данных свойств грунтов в ненасыщенных условиях [11] и уточнялись в процессе калибровки модели. После проведения калибровки были проведены прогнозные расчеты распространения загрязнения с территории полигона. Расчеты проводились в относительных концентрациях:
где C – концентрация консервативного загрязнителя в подземных водах водоносного горизонта или зоны аэрации; Другой важной задачей защиты окружающей среды, в которой существенную роль играют подземные воды, является определение устойчивости оползневых склонов и откосов. При решении таких задач следует учитывать, что фильтрация жидкости в насыщенной и ненасыщенной области оказывает существенное влияние на деформирование грунта. Задача устойчивости склонов с учетом фильтрации подземных вод может быть представлена в виде системы уравнений, состоящей из уравнения насыщенной-ненасыщенной фильтрации (1-2) и уравнений равновесия:
где
Учет деформаций в уравнении фильтрации достигается приравниванием источникового члена:
По вычисленным напряжениям определяется величина коэффициента запаса по напряжениям на площадках максимального сдвига
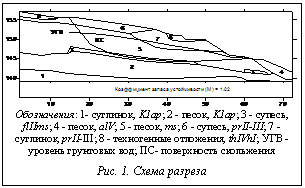
где Критической считается величина В подобной постановке задача рассмотрена в работе [4]. Первое отличие приведенной выше постановки от [4] состоит в том, что для описания движения воды здесь привлекается модель влагопереноса, в частности, модель Ван Генухтена. Второе отличие – модель из [3] более продвинута в область пластических деформаций, в то время как предлагаемая модель соответствует упругим деформациям. Для определения вектора полных перемещений и напоров решается численно краевая задача с помощью метода конечных элементов [5]. Результатом расчета является вектор полных перемещений, определенный в узловых точках деформируемой области и напор подземных вод (на каждый момент времени), по которым рассчитываются напряжения и деформации. В свою очередь, напряжения используются для расчета на площадках максимального сдвига коэффициента запаса устойчивости по напряжениям в каждом элементе. Изолинии равных значений коэффициента запаса, наложенные на чертеж объекта, выводятся в графические файлы (растровый и векторный). Приведем результаты расчетов склона, выполненные на основе численного моделирования, и сопоставим их с приближенным, но более простым в реализации методом предельного состояния. Расчеты выполнены для склона, схематический разрез которого показан на рисунке 1. Физико-механические свойства грунтов были получены по результатам изысканий. Параметры влагопереноса выбирались в соответствии с литологическим составом грунтов [11]. На рисунке 1, помимо геологического строения, показано положение уровня грунтовых вод, поверхность скольжения и коэффициент запаса устойчивости, рассчитанный с помощью метода предельного состояния Маслова-Берера в интерпретации Дорфмана [2, 6]. Следует отметить, что слабым звеном методов предельного состояния является неопределенность в положении поверхности скольжения, которая задается экспертно и зависит от опыта специалистов. Численное моделирование дает более объективные результаты. Результаты численного моделирования устойчивости склона методом конечных элементов приведены на рисунке 2. Таким образом, на рисунках 1 и 2 приведены результаты расчетов при различных подходах к оценке устойчивости. Во втором случае, в отличие от первого, рассчитывается, а не задается на основе экспертных оценок поверхность скольжения. Коэффициент запаса в обоих случаях определяется слабой супесью – flIIms.
В 80-е годы в НИИ "ВОДГЕО" был разработан пакет программ «GRSPVS» для выполнения комплексного гидравлического и гидрогеологического расчета береговых скважинных водозабо- ров [1]. Следует отметить, что гидрогеологическая часть расчетов в этом пакете основывалась на аналитических решениях, что не позволяло использовать пакет для сложных гидрогеологических условий, а использование упрощенной версии комплекса программ гидравлических расчетов систем подачи и распределения воды «ГРСПВ», не предусматривающей использование станций регулирования, обусловило весьма сложную и громоздкую методику проведения комплексных расчетов. Для ликвидации этих недостатков была начата разработка метода комплексного расчета скважинных водозаборов, основанного на совместном использовании конечно-разностных гидрогеологических моделей и модернизированных версий блока гидравлического расчета. К настоящему времени отработана программная реализация комплексного расчета для жесткого режима фильтрации, предусматривающая использование программ MODFLOW для геофильтрационного и «ГРСПВ-99» для гидравлического моделирования работы скважинных водозаборов. Программа «ГРСПВ-99» базируется на уникальном методе гидравлического расчета, позволяющем совместить решение задачи гидравлической "увязки" с определением параметров регулирующих элементов, включенных в расчетную схему и обеспечивающих требуемый режим работы рассчитываемой системы [7].
- требуемого пьезометра в диктующем узле; при этом диктующий узел автоматически выбирается из заданного набора контролируемых узлов; - требуемого перепада напоров между двумя заданными узлами сети (узлы не обязательно смежные); - требуемого расхода через регулятор. Для реализации комплексной модели была разработана программа-диспетчер, осуществляющая обмен информацией между геофильтрационной моделью (ГФМ) и блоком гидравлического расчета (БГР). ГФМ, получая в качестве исходных данных дебиты скважин
Определение параметров
где i – номер итерации; Ясно, что комплексная модель позволяет более глубоко анализировать процесс управления работой водозабора по сравнению с чисто гидравлической моделью или ГФМ. В частности, такой подход допускает моделирование процесса саморегулирования погружных насосов. Работоспособность модели была проверена на ряде реальных объектов. Одним из существенных ограничений данной версии комплексной модели является то, что в один блок ГФМ должна попадать только одна скважина. Кроме того, она позволяет анализировать только жесткий (стационарный) режим фильтрации. В настоящее время проводится отработка комплексной модели для нестационарных режимов фильтрации. Приведенное описание моделей и программ не закрывает весь спектр проблем, связанных с моделированием подземных вод. Надеемся, что публикации, список которых прилагается к статье, позволят войти в курс глубже. Список литературы 1. Алексеев В.С., Коммунар Г.М., Каримов Р.Х. и др. Рекомендации по применению ЭВМ для выполнения комплексных расчетов водозаборов подземных вод. – М.: ВНИИ ВОДГЕО, 1987. 2. Дорфман А.Г. Вопросы расчета устойчивости склонов и давления грунта на сооружения. // Инженерная геология. - 1984. - № 5. - С.47- 56. 3. Зарецкий Ю.К., Воробьев В.Н. Прогнозирование предельных состояний оснований фундаментов. Проблемы механики грунтов и инженерного мерзлотоведения. – М.: Стройиздат. -1991. - С. 97-105. 4. Зарецкий Ю.К., Ломбардо В.Н. Статика и динамика грунтовых плотин. - M.: Энергоатомиздат, 1983. - 256 с. 5. Зенкевич О. Метод конечных элементов в технике. - М.: Мир, 1975. - 539 с. 6. Маслов Н.Н. Механика грунтов в практике строительства (Оползни и борьба с ними). - М.: Стройиздат, 1977.- 320 с. 7. Мошнин Л.Ф., Каримов Р.Х. и др. Руководство по совершенствованию систем подачи и распределения воды городских водопроводов. 1-я ред. - М., НИИ "ВОДГЕО", 2000. 8. Chiang W.-H. and Kinzelbach W. Processing MODFLOW for Windows Version 5.0, Hamburg, 1998. 9. Doherty J., Brebber L. and Whyte P. (1994), PEST - Model-independent parameter estimation. User's manual. Watermark Computing. Australia. 10. Eviromental Simulation, Inc., 1996, Groundwater Vistas: Advanced Model Design & Analysis, Herdon, Virginia. 11. Leij, F.J., W.J. Alves, M. Th van Genuchten, and J.R. Williams, 1996, The UNSODA unsaturated soil hydraulic database, version 1.0, EPA report EPA/600/R-96/095, EPA National Risk Management Laboratory, G-72, Cincinnati, OH, USA, (http://www.ussl.ars.usda.gov/MODELS/ UNSODA.HTM). 12. McDonald, M. C. and A. W. Harbaugh, 1988. MODFLOW, A modular three-dimensional finite difference ground-water flow model, U. S. Geological Survey, Open-file report 83-875. 13. Pollock, D.W., 1994, Source Code and Ancillary Data Files for the MODPATH Particle Tracking Package of the Ground-Water Flow Model MODFLOW – Version 3, Release 1: U.S. Geological Survey Open-File Report 94-463, 2 p., two 3.5-inch diskettes. 14. Richards, D.R., and Jones, N.L. 1996. The DOD Groundwater Modeling System (GMS ):a conceptual model approach. Proceedings of the ASCE North American Water and Environment Congress, Anaheim, California, Jun 22-28. 15. Simunek J., T. Vogel and M. Th. Van Genuchten, 1992. The SWMS_2D code for simulating water flow and solute transport in two-dimensional variably saturated media. Version 1.1. Research Report No. 126, 169 p. U.S. Salinity Laboratory, USDA, ARS, Reverside, California. 16. Visual MODFLOW. Waterloo Hydrogeologec Inc., Waterloo, 1998. 17. Zheng, C. and P.P. Wang, 1998, MT3DMS, A modular three-dimensional multispecies transport model for simulation of advection, dispersion and chemical reactions of contaminants in groundwater systems. Documentation and user’s guide. Departments of Geology and Mathematics, University of Alabama. |
http://swsys.ru/index.php?id=626&lang=%E2%8C%A9%3Den&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:

 ; (1)
; (1)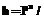 r
r ;
;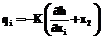 ; (2)
; (2) , (3)
, (3)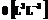 – объемное влагосодержание;
– объемное влагосодержание;  – поровое давление воды; rB – плотность воды; g – ускорение силы тяжести;
– поровое давление воды; rB – плотность воды; g – ускорение силы тяжести;  – давление воды, определяемое высотой водного столба;
– давление воды, определяемое высотой водного столба;  и
и  – концентрация загрязняющих веществ в водоносной толще и в источниках;
– концентрация загрязняющих веществ в водоносной толще и в источниках; – удельная интенсивность источников-стоков;
– удельная интенсивность источников-стоков;  – декартовы координаты (
– декартовы координаты ( – горизонтальная координата,
– горизонтальная координата,  – вертикальная координата);
– вертикальная координата);  – время;
– время;  и
и  – дифференциальная влагоемкость и коэффициент упругой емкости. Они равны:
– дифференциальная влагоемкость и коэффициент упругой емкости. Они равны: 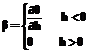 ,
,  ;
; – коэффициент фильтрации, который принимает следующие значения:
– коэффициент фильтрации, который принимает следующие значения: ,
,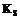 – коэффициент фильтрации в зоне полного насыщения;
– коэффициент фильтрации в зоне полного насыщения;  – относительная проницаемость, зависящая от насыщенности:
– относительная проницаемость, зависящая от насыщенности: . (4)
. (4) ,
, – минимальное влагосодержание;
– минимальное влагосодержание;  – влагосодержание при насыщенных условиях.
– влагосодержание при насыщенных условиях. ; (5)
; (5) .
. , (6)
, (6) ;
;  (
(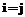 и
и  );
); 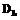 ,
, 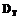
 – продольная и поперечная дисперсивность.
– продольная и поперечная дисперсивность. ,
, и
и  – концентрация того же вещества в фильтрате и фоновая.
– концентрация того же вещества в фильтрате и фоновая. r
r


 – осевые и сдвиговая деформации;
– осевые и сдвиговая деформации;  – напряжения нормальные и касательные – искомые компоненты тензора напряжений, определяемые в результате решения задачи упругого деформирования; rн=(1-m)rч+mrв; rч – плотность частиц скелета; деформации связаны с перемещениями следующими соотношениями:
– напряжения нормальные и касательные – искомые компоненты тензора напряжений, определяемые в результате решения задачи упругого деформирования; rн=(1-m)rч+mrв; rч – плотность частиц скелета; деформации связаны с перемещениями следующими соотношениями: .
.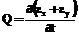 .
. [3]:
[3]:
 ,
, – сцепление и угол внутреннего трения – физико-механические свойства грунта.
– сцепление и угол внутреннего трения – физико-механические свойства грунта. .
.
 Традиционно анализ работы скважинных водозаборов проводится в два этапа. На первом этапе, используя геофильтрационные модели, определяются дебиты скважин и положения динамических уровней воды в них. При этом учитываются только гидрогеологические аспекты работы водозабора. На втором этапе, считая дебиты скважин и положения динамических уровней воды в них заданными, анализируется работа сборного водовода и водоподъемного оборудования. При этом используется чисто гидравлическая модель системы сбора и транспортировки воды от скважин. Подобный подход не позволяет должным образом учесть тот факт, что водозаборы подземных вод представляют собой комплекс водозаборных сооружений и сооружений системы подачи воды от скважин, все элементы которого гидравлически взаимосвязаны. Эта связь проявляется в том, что производительность водоподъемного оборудования зависит как от гидравлических характеристик всех элементов водозабора (включая и характеристики водоподъемного оборудования скважин), так и от положения динамических уровней воды в скважинах, а те, в свою очередь, определяются количеством отбираемой из скважины воды. Поэтому, когда в реальных условиях наблюдается колебание уровней (обусловленное сработкой запасов подземных вод, изменением гидрогеологических условий в области питания и разгрузки пласта и, наконец, возмущениями, вызываемыми действиями самих скважин), производительность самих установок изменяется. Насколько ощутимы будут эти изменения, зависит от гидрогеологических условий и гидравлических характеристик элементов, составляющих систему. Назначение дебитов скважин только по результатам геофильтрационного моделирования без учета ограничений, накладываемых совместным влиянием гидравлических характеристик насосного оборудования и сборного водовода, может потребовать неоправданного завышения требований к характеристикам насосов и усложнения способов регулирования работы скважинного водозабора. Все это обусловливает необходимость комплексного подхода к проектированию и эксплуатации водозаборов подземных вод с учетом не только гидрогеологических, но и гидравлических аспектов работы скважинных водозаборов, что, в свою очередь, предполагает совместное использование геофильтрационной и гидравлической моделей скважинных водозаборов.
Традиционно анализ работы скважинных водозаборов проводится в два этапа. На первом этапе, используя геофильтрационные модели, определяются дебиты скважин и положения динамических уровней воды в них. При этом учитываются только гидрогеологические аспекты работы водозабора. На втором этапе, считая дебиты скважин и положения динамических уровней воды в них заданными, анализируется работа сборного водовода и водоподъемного оборудования. При этом используется чисто гидравлическая модель системы сбора и транспортировки воды от скважин. Подобный подход не позволяет должным образом учесть тот факт, что водозаборы подземных вод представляют собой комплекс водозаборных сооружений и сооружений системы подачи воды от скважин, все элементы которого гидравлически взаимосвязаны. Эта связь проявляется в том, что производительность водоподъемного оборудования зависит как от гидравлических характеристик всех элементов водозабора (включая и характеристики водоподъемного оборудования скважин), так и от положения динамических уровней воды в скважинах, а те, в свою очередь, определяются количеством отбираемой из скважины воды. Поэтому, когда в реальных условиях наблюдается колебание уровней (обусловленное сработкой запасов подземных вод, изменением гидрогеологических условий в области питания и разгрузки пласта и, наконец, возмущениями, вызываемыми действиями самих скважин), производительность самих установок изменяется. Насколько ощутимы будут эти изменения, зависит от гидрогеологических условий и гидравлических характеристик элементов, составляющих систему. Назначение дебитов скважин только по результатам геофильтрационного моделирования без учета ограничений, накладываемых совместным влиянием гидравлических характеристик насосного оборудования и сборного водовода, может потребовать неоправданного завышения требований к характеристикам насосов и усложнения способов регулирования работы скважинного водозабора. Все это обусловливает необходимость комплексного подхода к проектированию и эксплуатации водозаборов подземных вод с учетом не только гидрогеологических, но и гидравлических аспектов работы скважинных водозаборов, что, в свою очередь, предполагает совместное использование геофильтрационной и гидравлической моделей скважинных водозаборов.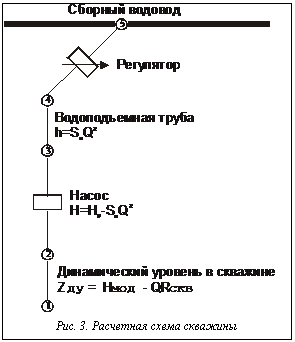 Для учета взаимного влияния скважин как через пласт, так и через сборный водовод, каждая скважина в гидравлической модели изображается четырьмя участками (рис. 3). Участок, соединяющий узлы расчетной схемы 1 и 2, отображает воздействие динамических уровней воды в скважине на работу водозабора, участок (2-3) отображает гидравлическую характеристику погружного насоса, участок (3-4) отображает гидравлическую характеристику водоподъемной трубы, участок (4-5) отображает гидравлическую характеристику регулирующей арматуры. Выбирая соответствующий закон регулирования среди поддерживаемых программой «ГРСПВ-99», можно не только проводить расчеты по всем задачам, перечисленным в [16], но и решать некоторые задачи, связанные с калибровкой комплексной модели и выбором режимов работы водозабора. «ГРСПВ-99» позволяет определить напор, развиваемый (гасимый) регулятором, при котором обеспечивается поддержание:
Для учета взаимного влияния скважин как через пласт, так и через сборный водовод, каждая скважина в гидравлической модели изображается четырьмя участками (рис. 3). Участок, соединяющий узлы расчетной схемы 1 и 2, отображает воздействие динамических уровней воды в скважине на работу водозабора, участок (2-3) отображает гидравлическую характеристику погружного насоса, участок (3-4) отображает гидравлическую характеристику водоподъемной трубы, участок (4-5) отображает гидравлическую характеристику регулирующей арматуры. Выбирая соответствующий закон регулирования среди поддерживаемых программой «ГРСПВ-99», можно не только проводить расчеты по всем задачам, перечисленным в [16], но и решать некоторые задачи, связанные с калибровкой комплексной модели и выбором режимов работы водозабора. «ГРСПВ-99» позволяет определить напор, развиваемый (гасимый) регулятором, при котором обеспечивается поддержание: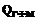 , выдает в качестве результата напоры в блоках, соответствующих скважинам. Диспетчер по дебитам и напорам определяет уровни воды в скважинах и передает их в БГР. Переход от уровней в блоках ГФМ
, выдает в качестве результата напоры в блоках, соответствующих скважинам. Диспетчер по дебитам и напорам определяет уровни воды в скважинах и передает их в БГР. Переход от уровней в блоках ГФМ  к динамическим уровням воды в скважинах
к динамическим уровням воды в скважинах  при известных дебитах скважин
при известных дебитах скважин 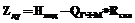 .
. , характеризующих сопротивление фильтров и призабойной зоны скважин и «схемное» сопротивление скважин, обусловленное дискретизацией, должно производиться из условия наилучшего соответствия наблюдаемых и полученных в результате ГФМ значений
, характеризующих сопротивление фильтров и призабойной зоны скважин и «схемное» сопротивление скважин, обусловленное дискретизацией, должно производиться из условия наилучшего соответствия наблюдаемых и полученных в результате ГФМ значений  . Диспетчер, получив дебиты от БГР, формирует новые значения дебитов для ГФМ по формуле:
. Диспетчер, получив дебиты от БГР, формирует новые значения дебитов для ГФМ по формуле: ,
,