Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Использование матричных квадродеревьев для хранения площадных картографических объектов
Аннотация:
Abstract:
| Автор: Крылов Б.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 20614 |
Версия для печати Выпуск в формате PDF (13.63Мб) |
Представление картографических объектов
Для эффективного решения конкретных задач объекты карты должны быть сведены в единую структуру, учитывающую специфику запросов. Например, транспортную сеть удобнее всего хранить в виде графа (это обеспечивает быструю обработку запросов вида «найти кратчайший маршрут из т. A в т. B»), а информация о рельефе может храниться в виде триангуляции. Точечные объекты могут быть сведены в одну из структур, использующих иерархическое разбиение пространства. Это позволяет эффективно выполнять запросы «найти ближайший к указанной точке объект», «найти все объекты в заданном радиусе от ближайшей точки» и т.п. В данной статье предлагается модификация матричных квадродеревьев, позволяющая использовать эту структуру данных для хранения многоугольников. Это дает возможность оптимизировать выполнение следующих массовых запросов для площадных объектов: «найти объекты, содержащие заданную точку», «найти объекты, находящиеся на определенном расстоянии для заданной точки», «найти объект, ближайший к заданной точке». Матричные квадродеревья
Каждый узел матричного квадродерева представляет квадратную область и определяется следующим образом: УказательНаУзелДерева = ^УзелДерева УзелДерева = record case child_type(internal,leaf) of internal:(pNO,pSO,pSW,pNW:УказательНаУзелДерева); leaf:(lsptNO,lsptSO,lsptSW,lsptNW:СписокТочек); end Матричное квадродерево строится следующим образом: представляемая карта покрывается сеткой ( Таким образом, с помощью описанной структуры возможно организовать объекты, локализуемые в точке. В качестве примера приведем следующий набор из пяти точек на сетке размером 8 Легко видеть, что процедуры добавления, удаления и поиска точки в матричном квадродереве имеют эффективность по времени, линейную относительно уровня детализации карты (высоты дерева). Особый интерес представляет задача отыскания списка точек, попадающих в заданную область. К ней же сводится и задача нахождения отдельной точки по ее координатам, поскольку все практические картографические данные имеют погрешность, и в этом случае также необходимо задавать область поиска. Матричные квадродеревья обеспечивают очень высокую скорость обработки таких запросов по сравнению с другими структурами для представления пространственных данных – O(N+ На рисунке 3 приведен пример запроса «получить все объекты в указанном радиусе от точки» в матричном квадродереве, представляющего область 8´8. Область поиска – круг с центром в точке О(4.6;5.8) и радиусом 1.1. Заштрихованы подобласти, рассматриваемые в ходе запроса. Результат – точки B,D и С. Эффективность работы со структурой по времени складывается из времени выполнения основных запросов, времени модификации структуры и времени, необходимого для ее создания из картографических примитивов. Матричные квадродеревья являются оптимальной структурой для работы с относительно равномерно распределенной картографической информацией. Детальное описание алгоритмов работы с матричными квадродеревьями дано в [1]. Хранение площадных объектов в расширенных матричных квадродеревьях Площадные картографические объекты в общем случае являются комбинацией многоугольников. Модифицируем матричные квадродеревья для хранения многоугольников. Сетка, задаваемая деревом, будет рассекать контур многоугольника на отрезки. Отрезок содержит: указатель на соответствующий объект карты, номера начальной и конечной точек, а также признак того, какая часть (левая или правая) разделенного отрезком квадрата лежит внутри объекта. Листья дерева будут содержать списки отрезков, попадающих в соответствующую ячейку. Внутренние узлы содержат списки указателей на площадные объекты, полностью накрывающие область данного узла. Это позволяет выполнять запросы «найти площадные объекты, в которые попадает данная точка» и избежать при этом излишнего разрастания де- рева.
Структура узла расширенного матричного дерева имеет вид: УказательНаУзелДерева = ^УзелДерева УзелДерева = record { списки площадных объектов, целиком } { накрывающих соответствующие подобласти } lsplNO,lsplSO,lsplSW,lsplNW:СписокУказателейНаМногоугольники; { флаги присутствия типов в подобластях } nNO,nSO,nSW,nNW:DWORD; case child_type(internal,leaf) of internal:(pNO,pSO,pSW,pNW:УказательНаУзелДерева); leaf:(lssgNO,lssgSO,lssgSW,lssgNW:СписокОтрезковКонтура); end Приведем схему алгоритма добавления многоугольника в расширенное матричное квадродерево. Работа с линейными списками организуется стандартным образом. {Глобальные переменные} var gnHeight:integer; {высота дерева} gdSide:real; {длина стороны представляемой квадратной области} gpRoot:УказательНаУзелДерева; {корень дерева} procedure ДобавитьМногоугольник( poly: Многоугольник;{добавляемый объект} lsNode: СписокОтрезковКонтура; { добавляемые отрезки контура } pNode: УказательНаУзелДерева; { текущий узел дерева } ptNode: Точка; { координаты центра области текущего узла } nLevel: integer;{ текущий уровень }) var lsNO,lsNW,lsSO,lsSW: СписокОтрезковКонтура; ptNO,ptSO,ptSW,ptNW: Точка; { Центры подобластей. } dCell:real { длина стороны ячейки данного уровня} procedure Ветвь(var nQD:DWORD; var lsQD:СписокОтрезков; var ptQD:Точка; var pQD:УказательНаУзелДерева var lsplQD:СписокУказателейНаМногоугольники; var lssgNO:СписокОтрезков) begin if СписокНеПуст(lsQD) then begin if nLevel=gnHeight then ДобавитьВСписок(lssgQD,lsQD) else begin if pQD=nil then new(pQD); ДобавитьМногоугольник(poly,lsQD,pQD,ptQD,nLevel+1) end nQD := nQD or nType end else if ТочкаВнутриЧастиМногоугольника(ptQD,РазмерЯчейки(nLevel+1),lsNode) then begin ДобавитьВСписок(lsplQD,@poly); nQD := nQD or nType end; end begin dCell:=РазмерЯчейки(nLevel) { Вычисление центров подобластей } ptNO.X:=ptNode.X+dCell; ptNO.Y:=ptNode.Y+dCell; ptSO.X:=ptNode.X-dCell; ptSO.Y:=ptNode.Y+dCell; ptSW.X:=ptNode.X-dCell; ptSW.Y:=ptNode.Y-dCell; ptNW.X:=ptNode.X+dCell; ptNW.Y:=ptNode.Y-dCell; Получить списки отрезков lsNO,lsNW,lsSO,lsSW для соответствующих подобластей ячейки (ptNode,dCell) путем рассечения отрезков из списка lsNode Ветвь(pNode^.nNO,lsNO,ptNO,pNode^.pNO,pNode^.lsplNO,pNode^.lssgNO); Ветвь(pNode^.nNW,lsNW,ptNW,pNode^.pNW,pNode^.lsplNW,pNode^.lssgNW); Ветвь(pNode^.nSO,lsSO,ptSO,pNode^.pSO,pNode^.lsplSO,pNode^.lssgSO); Ветвь(pNode^.nSW,lsSW,ptSW,pNode^.pSW,pNode^.lsplSW,pNode^.lssgSW); end. {Вызов процедуры добавления многоугольника} var x:Многоугольник ДобавитьМногоугольник(x,Контур(x),gpRoot,Точка(gdSide/2,gdSide/2),0); Время, необходимое на добавление многоугольника, складывается из времени, необходимого на построение рассечения контура на каждом уровне, и числа уровней. Поскольку на рассечение требуется время, линейное от числа точек, и совокупное число точек в отрезках на всех уровнях одинаково, то время работы приведенного алгоритма есть O(N*h), где N – число точек в контуре, а h – высота дерева. Выполнение запросов «найти объекты, находящиеся на определенном расстоянии для заданной точки», «найти объект, ближайший к заданной точке» происходит так же, как и в случае обычных матричных квадродеревьев [1]. Специфическим запросом для многоугольников является поиск всех объектов карты, которые содержат заданную точку. Приведем схему алгоритма, реализующего данный запрос.
pNode: УказательНаУзелДерева { текущий узел дерева } ptNode: Точка; { координаты центра области текущего узла } nMask: DWORD; { маска классов для поиска } nLevel: integer;{ текущий уровень } var bN,bE:boolean { признаки квадранта точки поиска } pQD: УказательНаУзелДерева { текущее поддерево } nQD: DWORD{ маска классов для поддерева } dCell:real{ длина стороны ячейки данного уровня} plsplQD: ^СписокУказателейНаМногоугольники plssgQD: ^СписокОтрезковКонтура begin { Определить квадрант точки поиска } bN := ptFind.X>ptNode.X bE := ptFind.Y>ptNode.Y dCell:=РазмерЯчейки(nLevel) { Выбор переменных для соответствующего квадранта } if bN and bE then begin pQD:=pNode^.pNO; plssgQD:= @pNode^.lssgNO plsplQD:= @pNode^.lsplNO; nQD:=pNode^.nNO ptNode.X:=ptNode.X+dCell; ptNode.Y:=ptNode.X+dCell end; if not bN and bE then begin pQD:=pNode^.pSO; plssgQD:= @pNode^.lssgSO plsplQD:= @pNode^.lsplSO; nQD:=pNode^.nSO ptNode.X:=ptNode.X-dCell; ptNode.Y:=ptNode.X+dCell end; if not bN and not bE then begin pQD:=pNode^.pSW; plssgQD:= @pNode^.lssgSW plsplQD:= @pNode^.lsplSW; nQD:=pNode^.nSW ptNode.X:=ptNode.X-dCell; ptNode.Y:=ptNode.X-dCell end; if bN and not bE then begin pQD:=pNode^.pNW; plssgQD:= @pNode^.lssgNW plsplQD:= @pNode^.lsplNW; nQD:=pNode^.nNW ptNode.X:=ptNode.X+dCell; ptNode.Y:=ptNode.X-dCell end; if nLevel<>gnHeight then begin { Игнорировать поддеревья, не содержащие } { объектов запрашиваемых классов} if (nMask and nQD)=0 then exit; Выдать все такие многоугольники из списка plsplQD^, что их класс входит в nMask. ПоискМногоугольников(ptFind,pQD,ptNode,nMask,nLevel+1); end else begin
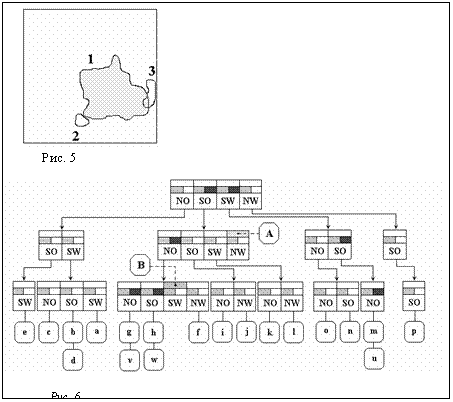
По очереди рассмотреть все многоугольники, отрезки контуров которых находятся в списке plssgQD^, и выдать те, в которые попадает точка ptFind и которые имеют класс, входящий в nMask. end end. {Вызов процедуры поиска многоугольника} var pt:Точка; nMask:DWORD ПоискМногоугольников(pt,gpRoot,Точка(gdSide/2,gdSide/2),nMask,0); На рисунках 4-6 приведены примеры хранения площадных объектов в расширенном матричном квадродереве. Исходная карта (рис. 4) содержит три площадных объекта (1-3) двух классов: к первому принадлежит 1, ко второму – 2 и 3. Для их хранения строится дерево высоты 3. При этом объект 1 разделяется на отрезки a,b…p и внутренние области A и B, объект 2 представляет отрезок u, а объект 3 – отрезки v и w. Полученное разбиение изображено на рисунке 5. На рисунке 6 приведено соответствующее дерево (пустые указатели в узлах не показаны). Каждый узел содержит поле из двух бит, отмечающих присутствие объектов соответствующих классов в поддеревьях. Данная структура также может использоваться для хранения линейных объектов, с тем только изменением, что списки «полностью накрывающих объектов» для внутренних узлов дерева становятся ненужными. Основной тип запроса здесь будет «найти линию, ближайшую к заданной точке». Автор выражает благодарность своему научному руководителю кандидату физико-математических наук, доценту Дехтярю М.И. за обсуждение статьи и полезные замечания. Список литературы 1. Subrahmanian V.S. Principles of Multimedia Database Systems. Morgan Kaufmann Publishers, Inc. San Francisco. 1997. 2. Препарата Ф. Шеймос М. Вычислительная геометрия: Введение. - М.: Мир, 1989. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=632&like=1&page=article |
Версия для печати Выпуск в формате PDF (13.63Мб) |
| Статья опубликована в выпуске журнала № 3 за 2003 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формулировка задачи планирования линейных и циклических участков кода
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Зарубежные базы данных по программным средствам вычислительной техники
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Система поддержки принятия решений по планированию профессиональной структуры подготовки специалистов
Назад, к списку статей



 При построении электронной картографической системы важную роль играют задачи, связанные с хранением картографических объектов и доступом к ним. Картографические объекты содержат описание пространственного положения (метрику) и прочие данные (семантику). Реляционные базы данных могут эффективно использоваться для работы с семантикой объектов, в то время как для работы с метрикой требуются более сложные приемы. Картографические объекты по своему пространственному положению делятся на следующие типы: точечные объекты (город, корабль, отметка высоты), линейные объекты (изобаты, изогипсы) и площадные объекты (суша, лес). Во всех перечисленных случаях ме- трика объекта состоит из набора точек. Как правило, точки задаются в прямоугольных координатах для выбранной картографической проекции.
При построении электронной картографической системы важную роль играют задачи, связанные с хранением картографических объектов и доступом к ним. Картографические объекты содержат описание пространственного положения (метрику) и прочие данные (семантику). Реляционные базы данных могут эффективно использоваться для работы с семантикой объектов, в то время как для работы с метрикой требуются более сложные приемы. Картографические объекты по своему пространственному положению делятся на следующие типы: точечные объекты (город, корабль, отметка высоты), линейные объекты (изобаты, изогипсы) и площадные объекты (суша, лес). Во всех перечисленных случаях ме- трика объекта состоит из набора точек. Как правило, точки задаются в прямоугольных координатах для выбранной картографической проекции.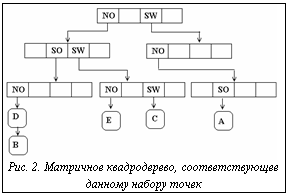 Современная технология создания и хранения географической информации требует относительно равномерной плотности распределения данных по карте. Например, отметки высот распределяются равномерно по всей картографируемой территории. Для хранения относительно равномерно распределенных пространственных данных широко используются матричные квадродеревья (MX-quadtrees). Важное преимущество матричных квадродеревьев перед другими структурами для хранения географических данных (k-d деревьями, точечными квадродеревьями [1,2]) в том, что форма и высота матричного квадродерева не зависят от числа объектов и порядка их вставки. Кроме того, матричные квадродеревья обеспечивают эффективные алгоритмы удаления и поиска.
Современная технология создания и хранения географической информации требует относительно равномерной плотности распределения данных по карте. Например, отметки высот распределяются равномерно по всей картографируемой территории. Для хранения относительно равномерно распределенных пространственных данных широко используются матричные квадродеревья (MX-quadtrees). Важное преимущество матричных квадродеревьев перед другими структурами для хранения географических данных (k-d деревьями, точечными квадродеревьями [1,2]) в том, что форма и высота матричного квадродерева не зависят от числа объектов и порядка их вставки. Кроме того, матричные квадродеревья обеспечивают эффективные алгоритмы удаления и поиска. на
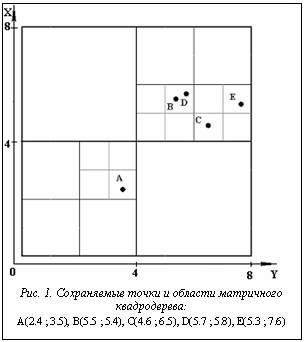
на  8. На рисунке 1 показано расположение точек и области МХ-квадродерева высоты 3, соответствующего данному набору. На рисунке 2 приводится изображение этого дерева.
8. На рисунке 1 показано расположение точек и области МХ-квадродерева высоты 3, соответствующего данному набору. На рисунке 2 приводится изображение этого дерева. ), где N – число выданных точек, h – высота дерева. Алгоритм поиска заключается в рекурсивном просмотре дерева с исключением узлов, не имеющих пересечения с областью поиска.
), где N – число выданных точек, h – высота дерева. Алгоритм поиска заключается в рекурсивном просмотре дерева с исключением узлов, не имеющих пересечения с областью поиска.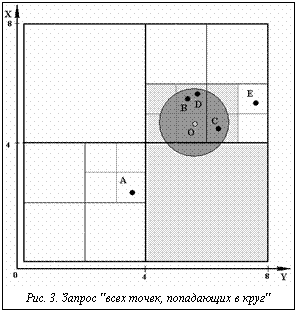 Однотипные картографические объекты образуют классы (например, классы изобата, квартал). Близкие по смыслу классы образуют семантические слои (например, слои гидрография, растительность, населенные пункты). Можно получить значительный выигрыш в памяти, храня в одном дереве объекты, относящиеся ко всему слою. При этом, если в структуру узла включить признак вхождения для каждого класса представляемых объектов, при запросах сохраняется возможность рассматривать каждый класс независимо от других. Учитывая, что число классов объектов в слое обычно не превосходит двух десят- ков, битового поля в 32 бита будет вполне достаточно, и размер структуры увеличится несущественно.
Однотипные картографические объекты образуют классы (например, классы изобата, квартал). Близкие по смыслу классы образуют семантические слои (например, слои гидрография, растительность, населенные пункты). Можно получить значительный выигрыш в памяти, храня в одном дереве объекты, относящиеся ко всему слою. При этом, если в структуру узла включить признак вхождения для каждого класса представляемых объектов, при запросах сохраняется возможность рассматривать каждый класс независимо от других. Учитывая, что число классов объектов в слое обычно не превосходит двух десят- ков, битового поля в 32 бита будет вполне достаточно, и размер структуры увеличится несущественно.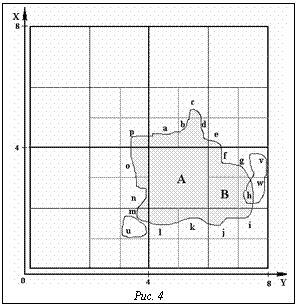 procedure ПоискМногоугольников(ptFind:Точка { точка поиска }
procedure ПоискМногоугольников(ptFind:Точка { точка поиска }