Анимация воксельной сцены
| Бобков В.А. (bobkov@iacp.dvo.ru) - Институт автоматики и процессов управления ДВО РАН (зав. лабораторией), Владивосток, Россия, доктор технических наук, Роньшин Ю.И. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
В отличие от статической визуализации, где решается задача точного определения видимости объектов сцены, в анимационной визуализации основной задачей является повышение скорости формирования и вывода последовательности кадров с возможной допустимой ошибкой в определении видимости. Существует несколько путей ускорения визуализации, которые в разных вариантах и комбинациях реализуются в современных алгоритмах. Первый из них – разделение всего объема вычислений на два этапа: предварительные вычисления и непосредственное формирование последовательности изображений с возможной их визуализацией в интерактивном режиме. В этом случае значительная доля трудоемкости вычислений переносится на предварительный этап, за счет чего собственно визуализация может осуществляться "на лету". Примером реализации такого подхода является вычисление PVS (потенциально видимых наборов) [1,2]. Другой, активно развиваемый сегодня путь, – использование вспомогательных структур данных, облегчающих поиск видимых объектов и направленных в целом на снижение зависимости вычислительной эффективности алгоритмов от количества объектов в сцене. Так, в алгоритме иерархического z-буфера [3] используется z-пирамида и октантная структура данных [4,5], часто применяемая и во многих других алгоритмах. Также активно применяются BSP-структуры [6] и kd-trees [7], которые в сочетании с методом преград (occlusion culling method/occlusion calculations/occlusion trees) [8,9] обеспечивают быструю идентификацию невидимых частей сцены. Применение этих и других структур позволяет использовать в алгоритмах визуализации пространственную когерентность. Наконец, еще одно направление повышения скорости анимационной визуализации – реализация темпоральной когерентности, то есть использование результатов вычислений предыдущего кадра при формировании текущего. Как правило, это делается за счет повторного использования видимых элементов на предыдущем кадре. Например, в [10], как и в [3], вывод в текущем кадре начинается с видимого набора граней предыдущего кадра. Однако, если при этом не учитывать геометрию траектории просмотра сцены, могут возникать дефекты в формируемых таким способом изображениях. Например, в алгоритмах с использованием hierarchical occlusion maps и в некоторых других методах [11-13], обеспечивающих ускорение вычислений, не гарантируется вывод всех видимых объектов.
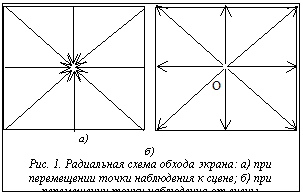
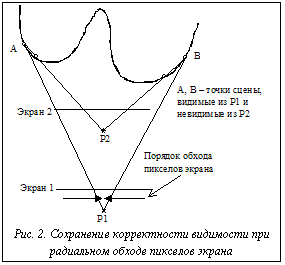
В настоящей работе предлагается подход к анимационной визуализации ранее реализованного октантного представления воксельной сцены [14], совмещающий в себе как предварительные вычисления (построение вспомогательной структуры данных), так и реализацию пространственной и темпоральной когерентности. Одновременно в предлагаемом методе анимации реализована и схема параллельных вычислений [15,16], обеспечивающая эффективную работу программы на многопроцессорной вычислительной системе. Организация режима анимации Рассматривается анимация типа "облет сцены" с предварительно заданной траекторией (контрольными точками) перемещения камеры наблюдения. Вдоль траектории будем различать опорные и промежуточные кадры. Для опорных кадров (положение и количество которых определяется некоторой заданной точностью отображения сцены и формой траектории) выполняется точное построение изображений предложенным алгоритмом трассировки лучей. В данной работе под трассировкой лучей понимается отслеживание лучей до первого пересечения с поверхностью объекта сцены. Промежуточными кадрами будем называть кадры между двумя соседними (по времени) опорными кадрами. Предлагаемая схема организации режима анимации направлена на повышение эффективности расчета промежуточных кадров. Предлагается алгоритм, реализующий темпоральную когерентность за счет повторного использования видимых точек (вокселов) текущего опорного кадра (одного или двух соседних) при формировании изображения промежуточного кадра. Формирование промежуточных кадров. При переходе от текущего кадра к соседнему большая часть точек, видимых на предыдущем кадре, остается видимой и на следующем. Одновременно небольшая часть точек, видимых на предыдущем кадре, становится невидимой на следующем кадре. Именно эти точки могут привносить ошибку в изображение, если отображать видимые точки предыдущего кадра на следующем, как это делается в некоторых алгоритмах, реализующих темпоральную когерентность. Как видно из геометрии, при небольших смещениях точки наблюдения, преодоление этого дефекта возможно двумя способами: 1) отображение видимых точек предыдущего опорного кадра на экран промежуточного кадра осуществляется в "правильном" порядке, обеспечивающем корректность их видимости при визуализации; 2) применение z-буферного принципа (сравнение расстояний при совпадении проекций точек) при отображении видимых точек на экран промежуточного кадра. При этом можно использовать видимые точки (вокселы) одного или двух соседних опорных кадров. Способ 1. Под правильным понимается такой порядок, когда для пары точек, лежащих на одном луче трассировки, отображается сначала невидимая, а затем видимая точка ("метод художника"). Отсюда возникает задача, которая решается в предлагаемом ниже алгоритме: для видимых точек текущего опорного кадра (результат трассировки сферической структуры по всем пикселам экрана) требуется найти такой порядок их проецирования на экран промежуточного кадра, который бы обеспечил корректность их видимости из точки наблюдения промежуточного кадра. Поскольку между множеством видимых точек и множеством пикселов экрана опорного кадра существует взаимно однозначное соответствие (трассировочный луч проходит через пиксел), сформулированная выше задача сводится к нахождению требуемого порядка обработки пикселов экрана текущего опорного кадра. Искомый порядок обработки пикселов экрана назовем схемой обхода экрана. Анализ видимости точек сцены при смещении точки наблюдения показывает, что существует два базовых движения точки наблюдения, которые влияют на изменение видимости. Первый тип соответствует движению точки наблюдения по нормали к плоскости экрана (к сцене и от сцены). В этом случае корректной, в смысле видимости, является радиальная схема обхода, показанная на рисунке 1 а,б. Точку O назовем центром симметрии. При таком порядке обхода точки, ставшие невидимыми на новом кадре, будут проецироваться на экран раньше, чем точки, их затеняющие (рис. 2). В итоге вклад в изображение нового кадра должны давать только видимые на новом экране точки. Второе базовое движение – смещение точки наблюдения параллельно плоскости экрана. Ему соответствует схема обхода, показанная на рисунке Процедура построения описанной схемы обхода экрана. Построим вектор P из центра проекций P1 текущего кадра в центр проекций P2 очередного кадра. Как показывает анализ видимости точек сцены при перемещении P2, искомый порядок обхода пикселов текущего экрана зависит от положения вектора P по отношению к плоскости экрана текущего кадра. Определяем точку пересечения вектора P с плоскостью экрана текущего кадра. Найденная точка Q на картинной плоскости является центром симметрии в искомой схеме обхода. В зависимости от положения точки Q по отношению к точке P1 на векторе P получается первый или второй вариант радиальной схемы обхода. Если уравнение отрезка P1P2 записать в векторной параметрической форме P=P1+t (P2-P1), то указанное выше условие можно выразить следующим образом: если tQ>0 (точка Q справа от точки P1), то имеем первый вариант схемы обхода, при tQ<0 (точка Q слева от точки P1) – второй. В случае параллельности вектора P1P2 и плоскости экрана текущего кадра выполняется проецирование P1P2 на экран и реализуется схема обхода, показанная на рисунке 3.
Формирование промежуточных кадров. Каждый из промежуточных кадров формируется в два этапа. На первом осуществляется проецирование видимых точек опорного кадра на экран промежуточного кадра в соответствии с полученным порядком обхода и закраска соответствующих пикселов (цвет выбирается из пикселов экрана опорного кадра). Второй этап формирования экрана промежуточного кадра – обработка оставшихся незакрашенными (после проецирования видимых точек текущего опорного кадра) пикселов экрана алгоритмом трассировки сферической структуры. Второй способ реализации темпоральной когерентности, как было указано выше, – применение z-буферного принципа – сравнение расстояний для перекрывающихся точек (вокселов). При этом промежуточные кадры можно формировать с использованием видимых точек только предыдущего опорного кадра или двух соседних (предыдущего и следующего). Во втором случае оба множества точек можно объединить в одно и выполнять их обработку в произвольном порядке. И, наконец, третий способ, который был реализован и показал наилучший результат, объединяет оба вышеописанные. А именно, используется пара соседних опорных кадров. Для каждого из них определяется схема обхода, в соответствии с которой отображаемые вокселы сортируются в порядке возрастания их удаленности от точки наблюдения, а затем осуществляется проецирование вокселов на экран с применением z-буферного принципа. Это повышает скорость работы z-буферного алгоритма в сравнении с произвольным порядком отображения вокселов на экран. Величина смещения между опорными кадрами вдоль траектории наблюдения может быть значительной. Но поскольку она зависит от геометрического характера сцены и автоматически не определяется, в данной программной реализации количество опорных кадров задается пользователем как настраиваемый параметр. В таблице 1 приведены результаты экспериментов по сравнению предложенного метода расчета анимационных кадров с базовым методом (независимый расчет кадров методом трассировки лучей). Визуализировалась сцена средней сложности с глубиной октантного дерева 8 при разрешении экрана 1280´960´32 для двух вариантов выбора опорных кадров на анимационной последовательности из 200 кадров. Параметры производительности используемой вычислительной техники в данном случае не приводятся, поскольку сравнение носит относительный характер. Вариант 1: всего кадров 200, опорных кадров 18 (через 20 град.). Вариант 2: всего кадров 200, опорных кадров 8 (через 45 град.). Таблица 1
Как видно из таблицы, предлагаемый метод ускоряет вычисления в 3–3,5 раза в сравнении с базовым методом. Распараллеливание вычислений При статической визуализации с использованием трассировки лучей распараллеливание базировалось на разделении пикселов экрана (то есть трассируемых лучей). Такой подход становится труднореализуемым и недостаточно эффективным в случае предложенного метода анимационной визуализации. Основная причина заключается в том, что в нем наряду с трассировкой лучей используется и z-буферный алгоритм, неудобный для организации параллельных вычислений. Поэтому для распараллеливания обсчета анимационной последовательности кадров более естественным, с точки зрения простоты реализации и уменьшения накладных расходов, является разделение траектории перемещения камеры наблюдения. Поскольку с каждой парой смежных опорных кадров связана некоторая последовательность промежуточных кадров, целесообразно провести разбиение траектории по опорным кадрам. Тогда порцией работы, выделяемой каждому процессору, является обработка кадров между двумя соседними опорными. Предполагается, что количество опорных кадров превышает число используемых процессоров. В таблице 2 приведены результаты измерений по оценке эффективности на МВС 1000. Число используемых процессоров равно числу опорных кадров минус 1. Таблица 2
Как видно из таблицы, рассмотренная схема обеспечивает эффективность параллельных вычислений в среднем на уровне 75 %. Список литературы 1. Airey J., Rohlf J. and F. Brooks Jr. Towards Image Realism with Interactive Update Rates in Complex Virtual Building Environments. Symposium on Interactive 3D Graphics 90, pp. 41-50. 2. Cohen-Or D., Fibich G., Halperin D. and Zadicario E. Conservative Visibility and Strong Occlusion for Viewspace Partitioning of Densely Occluded Scenes. EUROGRAPHICS 98 pp. 243-253. 3. Greene N., Kass M. and Miller G. Hierarchical Z-Buffer Visibility. SIGGRAPH 93 pp. 231-238. 4. Kaplan M. The use of spatial coherence in ray tracing. In Technicuesfor Computer Graphics, ets., D. Rogers and R.A. Earnshaw, Springer-Verlag, New York, 1987. 5. Meagher D. Efficient synthetic image generation of arbitrary 3-D objects. Proc. IEEE Conf. On Pattern Recognation and Image Processing, 473-478, June 1982. 6. Naylor B. Partitioning tree image representation and generation from 3d geometric models. Graphics Interface 92 pp. 201-212. 7. Samet H.J. Design and analysis of Spatial Data Structures: Quadtrees, Octtrees, and other Hiereachical Methods. Addison Wesley, Redding, MA, 1989. 8. Luebke D. Georges C. Portals and Mirrors: Simple, Fast Evaluation of Potentially Visible Sets. Symposium on Interactive 3D Graphics 95 pp.105-106. 9. Hey H., Purgathofer W. Occlusion Culling Methods. State of the Art Report at Eurographics'01, Manchester, U.K., Sept. 2001. 10. Боресков А.В. Метод иерархического s-буфера. // Программирование. - 1998. - №4. - С. 77-80. 11. Bartz D., Meissner M. and Hutner T. OpenGL-assisted Occlusion Culling for Large polygonal Models. Computer & Graphics 23 (1999) pp. 667-679. 12. Gotsman C., Sudarsky O. and Fayman J. Optimizied occlusion culling using five-dimensional subdivision. Computer & Graphics 23 (1999) pp. 645-654. 13. losowski J. and Silva C. The Prioritized-Layered Proection Algorithm for Visible Set Estimation. IEEE transactionson visualization and computer graphics vol. 6 no. 2 pp. 108-123, 2000. 14. Бобков В.А., Роньшин Ю.И. Алгоритм визуализации с трассировкой лучей в октантных деревьях. // Информационные технологии. - 2001. - №4. - С. 46-50 15. Бобков В.А., Роньшин Ю.И., Гуменников В.А. Параллельная обработка в алгоритмах визуализации с трассировкой лучей. // Программные продукты и системы. - 2001. - №1. - С. 27-30. 16. Бобков В.А., Роньшин Ю.И., Покудова Л.М., Харитонов Д.И. Анализ эффективности параллельной обработки в алгоритме визуализации с трассировкой лучей. // Информационные технологии. - 2002. - №6. - С. 50-53. |
http://swsys.ru/index.php?id=635&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- Средства обеспечения надежности функционирования информационных систем
- Опыт разработки и эксплуатации системы управления базами данных (DBS/R)
- Инструментальные и программные средства построения сетевых моделей

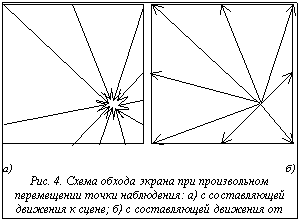 3. Произвольное перемещение точки наблюдения можно рассматривать как комбинацию двух базовых движений. Такому перемещению соответствует схема обхода со смещением центра симметрии в направлении плоской составляющей движения (см. рис. 4 а,б). Кроме указанных базовых движений возможно также вращение вектора просмотра (вращение плоскости экрана). В этом случае изменения видимости точек сцены не происходит, изменяется лишь пирамида видимости.
3. Произвольное перемещение точки наблюдения можно рассматривать как комбинацию двух базовых движений. Такому перемещению соответствует схема обхода со смещением центра симметрии в направлении плоской составляющей движения (см. рис. 4 а,б). Кроме указанных базовых движений возможно также вращение вектора просмотра (вращение плоскости экрана). В этом случае изменения видимости точек сцены не происходит, изменяется лишь пирамида видимости.
 Следующий этап – непосредственное определение порядка обхода пикселов экрана в соответствии с полученной схемой обхода экрана. Заметим, что рассматриваемая радиальная схема обхода экрана предполагает лишь то, что на каждом из лучей входящем/выходящем из центра симметрии две соседние точки экрана должны обрабатываться в порядке, определяемом направлением радиального луча. Оптимальной альтернативой непосредственному вычислению по Брезенхему цепочек пикселов с исключением их дублирования является, очевидно, сортировка всех пикселов по расстояниям до центра симметрии. Она удовлетворяет указанному выше условию и требует небольших вычислительных затрат. Полученный в результате сортировки порядок обхода пикселов будет, как было указано выше, одновременно и порядком обхода видимых точек опорного кадра. Он фиксируется в последовательном массиве в виде упорядоченного списка номеров пикселов экрана опорного кадра. Для ускорения обработки формируется также массив координат видимых точек, соответствующих пикселам экрана. Модификация рассмотренной схемы, направленная на увеличение допустимого смещения камеры наблюдения, – использование вместо одного опорного кадра двух соседних. В этом случае для второго опорного кадра берется схема обхода пикселов (и, соответственно, видимых точек – вокселов) в обратном направлении.
Следующий этап – непосредственное определение порядка обхода пикселов экрана в соответствии с полученной схемой обхода экрана. Заметим, что рассматриваемая радиальная схема обхода экрана предполагает лишь то, что на каждом из лучей входящем/выходящем из центра симметрии две соседние точки экрана должны обрабатываться в порядке, определяемом направлением радиального луча. Оптимальной альтернативой непосредственному вычислению по Брезенхему цепочек пикселов с исключением их дублирования является, очевидно, сортировка всех пикселов по расстояниям до центра симметрии. Она удовлетворяет указанному выше условию и требует небольших вычислительных затрат. Полученный в результате сортировки порядок обхода пикселов будет, как было указано выше, одновременно и порядком обхода видимых точек опорного кадра. Он фиксируется в последовательном массиве в виде упорядоченного списка номеров пикселов экрана опорного кадра. Для ускорения обработки формируется также массив координат видимых точек, соответствующих пикселам экрана. Модификация рассмотренной схемы, направленная на увеличение допустимого смещения камеры наблюдения, – использование вместо одного опорного кадра двух соседних. В этом случае для второго опорного кадра берется схема обхода пикселов (и, соответственно, видимых точек – вокселов) в обратном направлении.