Концептуальные положения модели динамического времени в контексте информационных технологий
| Тихомиров В.А. (tva@npo-rit.ru) - Тверской государственный технический университет, доктор технических наук, Тихомиров ВЛ.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Изучение проблемы времени связано с фундаментальным вкладом древнегреческой науки, идеи которой находят свое отражение в статической и динамической концепциях времени. Впервые отчетливо специфические проблемы динамического времени поставлены еще в IV веке Августином, который зафиксировал две центральные проблемы данной концепции времени – проблему существования прошлого, настоящего и будущего и проблему течения времени, или становления [1]. Однако последующая эволюция представлений о времени привела к полному господству статической концепции, в которой время представлено независимой непрерывной переменной с областью значений на вещественной оси. Такое абстрактное представление о времени, как о чем-то абсолютном, протекающем с равномерной скоростью, вошло в научное мировоззрение в XVII веке, благодаря трудам И. Барроу и И. Ньютона. Понятие абсолютного времени предоставляло возможность математикам, применявшим дифференциальное исчисление для изучения динамических процессов, не затрачивая усилий на размышления о том, какую размерность необходимо придавать независимой переменной. При этом проблема статуса существования временных событий и самих моментов времени не обсуждались. Более того, вопрос о времени рассматривался как полностью разрешенный, и только создатели специальной теории относительности продемонстрировали возможность новых представлений о времени. Столь важное событие не осталось незамеченным, и оказалось, что и без специальной теории относительности в науке накопился богатый экспериментальный материал, который свидетельствовал о необходимости отказа от понятия времени, введенного Ньютоном. В рамках зарождающейся парадигмы оказались востребованными альтернативные концепции. В первую очередь, фундаментальное положение древнегреческой науки о том, что время определяется движением, а не наоборот. Подход получил развитие в воззрениях Лейбница, трактовавшего время как порядок следования явлений. Причинно-следственные связи задают вполне определенную последовательность всем событиям, всем действиям и их результатам. Однако, несмотря на всю разумность и ясность идеи Лейбница, до сих пор ее никак не удавалось подкрепить конструктивными моделями. Привлекательна идея Александера: в ней в качестве датчика времени предлагается рассматривать изменение свойств объекта, а не его механическое движение [2]. Для реализации идеи Александера Н.И. Лобачевский, заменив слово «движение» словами «изменение свойства», сделал подход более приспособленным к математическому моделированию. Методологическая сложность модельной реализации концепции динамического времени состоит в том, что необходимо решение проблемы существования прошлого, настоящего и будущего. Для этого в работе [3] предлагается схема: Р – множество объектов, существующих в прошлом, Н – в настоящем и F – в будущем. Затем, по крайней мере, часть будущего должна стать настоящим, настоящее – полностью или частично – прошлым, а прошлое – увеличить сферу своего действия за счет "бывшего" настоящего. В результате из ряда Р, Н, F получится новый ряд Р', Н', F'. Логичный переход осуществляется на основе концепции метамоментов и введением нетривиального различия между М и М'. Процедура, обеспечивающая "своевременное" исчезновение М и преемственность между М и М', основывается на введении понятия квазиметамомента К. Далее автор [3] основное внимание уделяет способу реализации данной концепции. При этом в качестве основополагающего принципа берется интуиция, которая является не самым убедительным аргументом в ходе изучения одной из сложнейших характеристик материи. Поиск конструктивного основания связан с ответом на вопросы: "чем обусловлен механизм смены состояний?" и "куда направлен ход времени?". В свое время Лейбниц сформулировал положение, согласно которому время течет от причины к следствию. Больцман предложил гипотезу, по которой направление хода времени определяется общей тенденцией изолированной физической системы к достижению состояния термодинамического равновесия. Из последней концепции методологически важно то, что в ней в скрытой форме присутствует такая парная категория, как «определенность–неопределенность». В парных категориях проявляется дихотомия (и само движение обладает двойственностью) для выражения крайностей в объекте. Парные категории обособляют крайности объекта и становятся основой упорядочения его форм, что обеспечивает возможность выявления их единства и способов перехода одних форм в другие [4]. Анализ парных категорий, таких как «причина–следствие», «определенность–неопределенность», и категории «движение» показал, что движение по самой своей сущности есть явная неопределенность, которая выражается известной диалектической формулой "и да, и нет"» [5]. При этом в понятии неопределенность отражается момент тождества противоположностей в противоречивости движения [6]. Далее из анализа следует то, что философское понимание пространства и времени требует их рассмотрения в единстве с движением и материей. Однако из данного анализа автоматически не следует существование пространственно-временного континуума как чего-то единого. Скорее, категориальный анализ позволяет утверждать, что такое свойство объектов, как раздвоенность (дуализм как всеобщее проявление первого закона диалектики [7]) является необходимым моментом диалектической трактовки концепции времени. Диалектическая трактовка концепции динамического времени должна исходить из полярности категорий пространства и времени, что обеспечит понимание "перехода" от одного к другому. Любое движение предполагает так или иначе понимаемое изменение положения в пространстве, осуществляющееся в так или иначе понимаемом времени. При этом понятия пространства и времени соотносительные: в понятии пространства отражается координация различных внеположных друг другу объектов в один и тот же момент времени [4], а в понятии времени отражается координация сменяющих друг друга форм объектов или состояний процессов, детерминируемых системой законов, которые проявляются в определенном месте пространства. Пространство достаточно хорошо отождествляется с евклидовой структурой, которая характеризуется трехмерностью, симметрией и асимметрией, формой и размером, местоположением, расстоянием между телами, распределением вещества и поля. Специфические свойства времени как в статической, так и в динамической концепциях рассматриваются на уровне гипотез. Физический мир хорошо моделируется аффинным евклидовым пространством. Поскольку естественной единицы меры (длины) не существует, пространство рассматривается с точностью до выбора масштаба. Однако необходимо концептуальное видение изучаемой реальности, которое придаст фактам содержательный смысл. В статической концепции смысл придает структура, в которой моменты времени отождествляются с элементами числового множества (с отношением линейного порядка "раньше, чем" или "позже, чем"). Важно понимать, что при этом никаких допущений о природе времени в явном виде не делается, само время не исследуется, а временные понятия играют вспомогательную роль. Констатация того, что любая система координат пригодна в качестве основы описания происходящих явлений, не несет в себе никакого содержательного высказывания о свойствах и закономерностях любых явлений, в том числе и времени. Продуктивным является конструктивный подход к выбору системы координат. Данный подход характеризуется тем, что если какая-нибудь система координат выделяется, то это выделение должно происходить на основе установления факта, заключающегося в том, что те или иные процессы в соответствующих координатах допускают какое-то аналитическое описание, как правило, описание, отражающее развитие объекта как его главного свойства. Фундаментальное свойство определим исходя из единства пространства, времени и движения материи. При этом система должна обеспечивать экспликацию сущности движения (связанной с раскрытием неопределенности), которая выражается известной диалектической формулой "и здесь, и не здесь". Геометрическая модель, в которой осуществлена экспликация сущности движения, имеет вид, представленный на рисунке.
Для того чтобы показать, что данный подход не только способствует наглядной геометризации основных свойств времени, но и позволяет интерпретировать установленные пространственно-временные свойства материальных систем и получать новые результаты, осуществим некоторые теоретические обобщения. Далее формализация связана с реализацией идей Лейбница, трактовавшего время как порядок следования явлений. Причинно-следственные связи задают вполне определенную последовательность всем событиям, всем действиям и их результатам. Абстрагируясь от процесса, порождающего временную определенность событий, эту структуру следует рассматривать в динамике, выделив в системе координат инвариантные отношения ( R – элемент K2 находится в отношении R к элементу K3, где Ki – i-й метамомент), то есть закономерные причинно-следственные связи. Известно, что следствие влияет не только «вперед в будущее», но и в определенной временной перспективе «назад в прошлое», на производящую его причину. Эта темпоральная форма взаимодействия причины и следствия именуется принципом обратной связи. Следовательно, процесс модельного синтеза должен обеспечивать экспликацию сущности, отождествляемой с принципом обратной связи. На простейшей вербальной модели покажем возможность осуществления экспликации рассмотренных принципов. В качестве исходной посылки рассмотрим такой объект, как ЭВМ. Тогда для метамомента М3 на ось Т1 отображается тенденция совершенствования их базовых элементов (радиолампы); на оси Т2 представлены различные образцы машин первого поколения. След К3 метамомента М3 будем отождествлять с ЭВМ второго поколения, для которого на ось Т1 отображается тенденция совершенствования их базовых элементов (полупроводники); на оси Т2 представлены различные образцы ЭВМ второго поколения. Исходя из истории формирования специфической структуры ЭВМ, метамомент М3' отождествим с ЭВМ третьего поколения на микропроцессорной элементной базе. Принцип миниатюризации элементной базы, положенный в основу совершенствования ЭВМ, наглядно демонстрирует свойства причинно-следственной связи. Следствие (совершенствование элементной базы) влияет не только «вперед в будущее» (в качестве новой причины, рождающей новое следствие – ЭВМ нового поколения), но и в определенной временной перспективе «назад в прошлое», на производящую его причину – исчезновение старой элементной базы. Однако новая структурная организация не означает полного исчезновения старой; последняя сохраняется в виде определенной структуры (архитектура ЭВМ), в которой зафиксирована информация об определенном уровне развития системы. Следовательно, в каждом детерминированном структурном уровне организации системы всегда присутствует и информация о прошлом динамическом состоянии. Таким образом, структура самого процесса развития является особой сферой совместного проявления системного подхода и принципа развития. Однако содержательное описание не дает возможности подвергнуть анализу происходящие в системе процессы. Необходим переход от содержательного уровня формирования модели к уровню, обеспечивающему математическую экспликацию. В качестве методологического основания подобной экспликации выбрана гипотеза Больцмана. Согласно данной гипотезе направление хода времени определяется общей тенденцией изолированной физической системы к достижению состояния термодинамического равновесия. Однако это недостаточное условие для описания динамики неопределенности в реальных системах. Обычно утверждают, что «изолированная система» – это результат абстрагирующей деятельности. В процессе идеализации конструируются такие объекты, которые заведомо не могут существовать в объективной реальности. Однако построенная А. Эйнштейном первая космологическая модель на основе общей теории относительности продемонстрировала принципиальную возможность существования абсолютно изолированной реальной системы. Поэтому к «изолированной системе», которая полезна не только в термодинамике, но и в других теоретических концепциях, не следует подходить как к понятию, не отражающему никакого реального объекта. Строго говоря, указанную постановку всегда можно свести к взаимодействию двух систем, как правило, среды и собственно системы (или как определение процедуры интегрирования систем), образующих некую метасистему. Только при одновременном изучении их в масштабе метасистемы можно получить полное представление о взаимном влиянии обеих систем друг на друга и оценить это влияние. Поэтому практически важно уметь методически корректно разделять систему и среду. Основу такой методической корректности должна составлять концепция детерминизма, в пределах расширенного толкования которого причинный и системный подходы дополняют друг друга и дают более глубо- кую картину всеобщей связи явлений и процесса их развития. Дальнейшее становление конструктивистского метода связано с рассмотрением способов интегрирования нескольких сопоставимых систем в большую систему и с анализом понятия материальный объект. Для каждого объекта характерна совокупность свойств, через перечисление которых проявляется содержание понятия об объекте. Сочетание свойств объекта ставит его в определенные соотнесения с другими объектами. Соотнесение объектов происходит посредством введения бинарных понятий. Диалектический подход предполагает использование обобщенного бинарного понятия формы объекта. Форма объекта есть объект в одном из его состояний как единство всех его свойств, определяющих его качество и его отличия от других форм объекта. Таким образом, во-первых, все сведения о системе как объекте исследования описывают совокупность ее свойств; во-вторых, свойство – характеристика не одной формы объекта, а всех форм объекта; в-третьих, из общей теории систем известно, что в определенных условиях объект отождествляется с системой. Объект является системой, если его можно представить в виде упорядоченной пары множеств: множества соответствующих элементов, удовлетворяющих принципам целостности и эмерджентности, и множества отношений между этими элементами, определяющих структуру объекта. Становление структуры во времени, то есть процесс ее формирования, является одной из важнейших сущностных характеристик процесса развития, в том числе и интегрирования систем. Один из способов интегрирования систем состоит в определении соответствующей порождающей процедуры. Интегрированные при помощи такой процедуры системы являются метасистемами [8]. В зависимости от постановки задачи свойства сопоставимых систем могут трансформироваться. Исходя из того, что определение системы дается в терминах теории множеств, конкретизация общей задачи взаимодействия систем связана с теоретико-множественным описанием проблемы. Так, каждое свойство образует некоторое опорное множество Xi, тогда объединение UXi всех подобных множеств будет давать полное представление о системе в конкретный метамомент М. Познанные свойства проявляются через сведения об объектах. Параметры представляют количественно выраженные свойства. В простом виде они выступают посредством данных. Семантика данного описания находит отражение в назначении указателя (имени) х определяемого сведения. В контексте концепции динамического времени рассмотрим интерпретацию модели бедного по своему содержанию механического движения. В движении такого типа данные являются сведениями о траектории (указатель-имя), которые отображают становление структуры во времени Ti, имеющем такие имена-указатели, как метамоменты Мi, Кi и Мi'. При этом не сложно в терминах данной концепции описать процесс развития, если корректно и логически выверено применять положение о тождественности противоположностей ( R – метамомент K2 находится в отношении R к метамоменту K3, где отношение R определяет тождественность противоположностей). Данный подход позволяет описать явления, структурообразование которых подчиняется определенным периодическим, циклическим или спиралеобразным закономерностям. Реализация подхода допускает применение OLAP-технологии [9]. При использовании многомерной модели данных анализируемые формы концептуально представляются в виде гиперкуба, сторонами которого являются "измерения", в ячейках которого находятся сведения, характеризующие свойства. При этом на "измерениях" могут быть заданы иерархические отношения "один к многим", в соответствии с которыми производится агрегация данных. Становление (структурообразование в сложных системах) описывается в терминах эволюции, конкуренции, отбора и мутации. Поэтому теоретические положения и конструкции генетического алгоритма применимы для описания течения времени. Однако этих конструкций явно недостаточно для осуществления перехода к формализованному уровню описания процесса становления. Преодоление такого рода трудностей связано с решением проблемы диалектического “снятия” неопределенности [10]. Решение проблемы возможно на основе информационно-вероятностного подхода, позволяющего построить математическую модель для систем любого физического содержания. Способ построения математической модели был предложен в [10] и получил дальнейшее развитие в [11]. В основу модели положены принципы: общей теории непрерывных отображений топологических пространств; байесовского подхода; математической статистики и теории информации. При этом информационно-вероятностный подход позволяет осуществить переход к формализованному уровню описания процесса становления, уменьшает энтропию конкуренции, исключает тупиковые пути отбора, обеспечивает определение круга наиболее перспективных вариантов мутации. Список литературы 1. Молчанов Ю.Б. Четыре концепции времени в философии и физике. –М.: Наука, 1977. 2. Вернадский В.И. Пространство и время в неживой и живой природе. В кн.: Философские мысли натуралиста. – М.: Наука, 1988. 3. Анисов А.М. Время и компьютер. – М.: Наука, 1991. 4. Спиркин А.Г. Философия. – М.: Гардарика, 1998. 5. Готт В.С., Перетурин А.Ф. О некоторых философских предпосылках определения физического смысла волновой функции.// Философские вопросы квантовой физики. / Отв. ред. Омельяновский М.Э. ─М.: Наука, 1978. 6. Гречанова В.А. Неопределенность и противоречивость в концепции детерминизма. – Л.: ЛГУ, 1990. 7. Маркс К., Энгельс Ф. Капитал. // Собр. соч. В 9 т. – М.: Политиздат, 1987. - Т1. 8. Клир Дж. Системология (Автоматизация решения системных задач) – М.: Радио и связь, 1990. – 544 с. 9. Codd E.F., Codd S.B., Salley C.T. Providing OLAP (On-Line Analytical Processing) to User-Analysts:An IT Mandate. - E.F.Codd & Associates, 1993. 10. Мартыщенко Л.А., Тихомиров В.А. Вероятност- но-статистические методы праксеологического анализа разработок и оценки технических решений. -Л.: Изд-во ВАА, 1992. 11. Андреев Г.И., Тихомиров В.А. и др. Оценка интеллектуальной собственности. –М.: Финансы и статистика, 2002. |
http://swsys.ru/index.php?id=638&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
- Новый подход к проблеме коллективного выбора на базе удовлетворения взаимных требований сторон
- О программной реализации геоинформационных систем
- Разработка загрузчика программного обеспечения встроенной системы управления
- Механизм контроля качества программного обеспечения оптико-электронных систем контроля

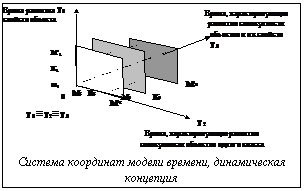 С целью наглядной геометризации основных свойств времени отметим следующее. Каждый объект как-то оформлен, структурно организован, содержателен. Содержание – это единство всех составных элементов объекта, его свойств, внутренних процессов, связей, противоречий и тенденций. В содержание входят не только составляющие тот или иной объект элементы, но и способ их связей, то есть структура. Структура – это не только способ расположения элементов объекта в пространстве, но и строение определенного процесса во времени, это определенная последовательность и ритм изменения процесса. Она есть единство содержания и формы. Представленная структура (система координат, у которой Т1≡ Т2≡ Т3, отражает основное положение диалектики – как становятся тождественными противоположности) – это способ выражения и существования содержания (системный подход к развитию форм объекта во времени). Геометрическую интерпретацию экспликации сущности диалектической формулы "и здесь, и не здесь" проведем на основе анализа структуры, представленной плоскостью 0 М2 М3. В этом случае К2, как след метамомента М2, отображает свойства объекта на оси времени Т2 ("и здесь"), при этом в силу того, что К2 порождает не только метамомент М2', но и метамомент М3, К2 является отображением К3, который в снятом виде отображает тенденцию развития объекта на оси времени Т3 ("и не здесь").
С целью наглядной геометризации основных свойств времени отметим следующее. Каждый объект как-то оформлен, структурно организован, содержателен. Содержание – это единство всех составных элементов объекта, его свойств, внутренних процессов, связей, противоречий и тенденций. В содержание входят не только составляющие тот или иной объект элементы, но и способ их связей, то есть структура. Структура – это не только способ расположения элементов объекта в пространстве, но и строение определенного процесса во времени, это определенная последовательность и ритм изменения процесса. Она есть единство содержания и формы. Представленная структура (система координат, у которой Т1≡ Т2≡ Т3, отражает основное положение диалектики – как становятся тождественными противоположности) – это способ выражения и существования содержания (системный подход к развитию форм объекта во времени). Геометрическую интерпретацию экспликации сущности диалектической формулы "и здесь, и не здесь" проведем на основе анализа структуры, представленной плоскостью 0 М2 М3. В этом случае К2, как след метамомента М2, отображает свойства объекта на оси времени Т2 ("и здесь"), при этом в силу того, что К2 порождает не только метамомент М2', но и метамомент М3, К2 является отображением К3, который в снятом виде отображает тенденцию развития объекта на оси времени Т3 ("и не здесь").