Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Нейропрограммный алгоритм предварительной обработки изображений в условиях шумов
Аннотация:
Abstract:
| Авторы: Самойлин Е.А. (es977@mail.ru) - Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия им. проф. Н.Е. Жуковского и Ю.А. Гагарина» (профессор), Воронеж, Россия, доктор технических наук, Серпенинов О.В. () - , Банников А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15568 |
Версия для печати Выпуск в формате PDF (1.36Мб) |
В последнее время большое внимание уделяется работам по созданию «интеллектуальных» оптических систем распознавания и обработки различных изображений. Это объясняется широкими возможностями систем искусственного видения, вплоть до передачи им некоторых функций, ранее посильных только человеку. Как правило, подобные распознающие системы осуществляют оптико-электронное преобразование изображения и последующую его обработку на основе различных алгоритмов обучения. Причем доказано, что для эффективного распознавания во многих случаях достаточно анализировать только его контурное изображение [1]. При этом внутренние элементы контуров объектов и фона можно исключить, так как они являются малоинформативными. Кроме того, в данном случае происходит уменьшение объемов памяти, необходимых для обработки изображений [1]. В настоящее время наиболее распространенными подходами, применяемыми для выделения границ объектов, являются статистический метод [2], выделение экстремумов кривизны изолиний [3] и использование теории нейронных сетей [4]. Однако в первых двух случаях для описания изображения требуется определить энергетическую функцию по достаточно большой окрестности точек, что ведет к резкому возрастанию вычислительных затрат. В тоже время наметился повышенный интерес к теории нейронных сетей, которая находит все большее применение для решения ряда инженерных задач [4,5]. Это объясняется возможностью решения нейронной сетью трудно формализуемых задач, именно таких, как распознавание изображений, и относительной простотой ее реализации на практике. В работе [4] приведены результаты моделирования нейронных сетей для решения задач определения границы раздела случайных полей на изображениях в условиях шумов. Полученные результаты свидетельствуют о преимуществах данных нейронных сетей перед оптимальной обработкой.
Рассмотрим задачу выделения границ объектов на изображениях однослойной нейронной сетью. Входной информацией для нейронов сети служит множество элементов полутоновой матрицы изображения, заданных непосредственно в виде набора значений зачерненности точек растра. Для определения границ объектов на выходе сети необходим синтез такой ее архитектуры, при которой будет оцениваться градационная близость соседних элементов матриц. То есть необходимо выбрать такую функцию, при которой ее локальные экстремумы соответствовали бы характерным фрагментам изображения. Подобная функция на участках, где изображение изменяется мало, является почти постоянной, а на участках, содержащих геометрические особенности, резко колеблется. В результате на выходе сети должны быть элементы матриц, которые относятся исключительно к контурным линиям объектов. Структура нейронной сети Для оптимального решения задачи определения информативных признаков полутоновой матрицы наиболее приемлема следующая архитектура сети.
Для определения принадлежности элементов растра к контурным линиям каждым нейроном сети в слое проводится сравнение его яркости с яркостью смежных элементов полутоновой матрицы. То есть производится нейронное дифференцирование яркостных элементов соседних пиксел. Принадлежность элемента полутоновой матрицы к контурной линии определяется на выходе слоя сети исходя из следующего условия [6]:
где: yi,j – сигнал на выходе нейрона Ni,j, N – количество строк матрицы изображения; M – количество столбцов матрицы изображения; Xi,j – вычисляемый в данный момент элемент изображения; Xi ± 1, j ± 1 – соседние элементы с вычисляемым; P – активационный порог, задаваемый эмпирически. На рисунке 1 для упрощения показан только один нейрон Ni,j, осуществляющий суммирование дифференциалов яркостей соседних элементов Xi ± 1, j ± 1 с центральным элементом Xi,j. Нейроны, соседние с Ni,j, смещены друг относительно друга на один элемент матрицы. Таким образом, центральный для одного нейрона элемент матрицы Xi,j для другого нейрона будет уже Xi+1,j (в случае смещения «вниз», на следующую строку). При обработке пикселей первых и последних строк и столбцов (i,j=1; i=N; j=M) нейроны имеют неполное число входов, равных количеству окружающих элементов данного пикселя. В случае обработки четырех угловых пикселей (X1,1, X1,M, XN,1, XN,M) у нейрона имеются всего три входа. Сигналы с выходов нейронов Ni ± 1, j ± 1 подаются на блок пороговой обработки yP (рис. 2), где для каждого элемента yi,j вычисляется условие (1). Активационный порог P устанавливается эмпирическим путем и может находиться в широких пределах. В случае «срабатывания» пороговой функции передачи, сигналы подаются на блок их умножения на входной сигнал, после чего на выходе нейросети формируются сигналы границ раздела После блока умножения сигналы границ раздела
Общая схема нейронной сети, приведенная на рисунке 2, для удобства представления также упрощена. Здесь показаны только соседние два элемента входа с центральным вместо восьми. В отличие от известных нейронных сетей для решения подобных задач [4,5] предлагаемая обладает сравнительной простотой структуры, так как имеет всего один слой; у нее отсутствуют какие-либо алгоритмы обучения и настройки весовых коэффициентов. В данном случае сама сеть за счет своей архитектуры решает задачу с оптимальным выбором выходных векторов. Результаты моделирования Моделирование рассмотренной нейронной сети проводилось в среде MathCAD версии 8.0 для Windows-2000. На вход сети подавалась полутоновая матрица исходного изображения размерностью 200´150 с яркостной градацией, равной 256. Матрица содержала изображение некоторых основных тестовых объектов (квадрат, треугольник, окружность, линии с различными углами наклона), с некоторым уровнем и интенсивностью зашумленности (рис. 3а). На рисунке 3б представлен результат выделения границ объектов данной полутоновой матрицы по широко известному цифровому алгоритму [6].
На рисунке 4а приведены результаты определения границ исходной полутоновой матрицы, показанной на рисунке 3а, однослойной нейронной сетью, аналогичной показанной на рисунке 2, без активационного блока F.
Таким образом, решение задачи определения границ объектов на изображениях с использованием нелинейной нейронной сети является наиболее предпочтительным по сравнению с линейной сетью и цифровой обработкой. Представленные в работе результаты моделирования алгоритма выделения границ объектов на изображениях в условиях шумов свидетельствуют об обоснованности применения нейросетевого подхода к подобным задачам и о принципиальной возможности замены традиционных алгоритмов обработки существенно более качественными – нейропрограммными. Нейронная сеть для оптимального решения задачи выделения границ является достаточно простой, имеет один слой нейронов, у нее отсутствуют алгоритмы обучения и настройки весовых коэффициентов. Однако даже такая нейронная сеть обеспечивает намного более качественное решение задачи выделения границ объектов с уменьшением уровня шумов. Список литературы 1. Кревецкий А.В. Распознавание трехмерных объектов по форме пространственных контуров // Автометрия. – 2001. – № 2. – С. 21-30. 2. Злобин В.К., Еремеев В.В., Васильев В.М. Стохастическая модель спутниковых изображений и ее использование для сегментации природных объектов // Там же. – С. 41-50. 3. Бобков В.А., Казанский А.В., Морозов М.А. Выделение размытых контуров на примере определения скорости течений по спутниковым изображениям // Там же. – С. 3-12. 4. Попело В.Д., Сирота А.А., Маслов О.В. Сравнительный анализ оптимального и нейросетевых алгоритмов определения границ раздела случайных полей при обработке изображений // Радиотехника. – 2001. – № 10. – С. 81-85. 5. Горбань А.Н., Дунин-Барковский В.Л., Миркес Е.М. и др. Нейроинформатика. – Новосибирск: Наука, 1998. – 224 с. 6. Бакут П.А., Колмогоров Г.С. Сегментация изображений: методы выделения границ областей // Зарубежная радиоэлектроника. – 1987. – № 10. – С. 25-47. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=639&page=article |
Версия для печати Выпуск в формате PDF (1.36Мб) |
| Статья опубликована в выпуске журнала № 2 за 2003 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Зарубежные базы данных по программным средствам вычислительной техники
- Эвристические и точные методы программной конвейеризации циклов
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
- Эволюционная модель формирования структур виртуальных предприятий
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
Назад, к списку статей



 Цель работы – обоснование применимости нейронной сети для выделения границ объектов на изображениях в условии шумов и сравнение результатов нейросетевой и цифровой обработки.
Цель работы – обоснование применимости нейронной сети для выделения границ объектов на изображениях в условии шумов и сравнение результатов нейросетевой и цифровой обработки.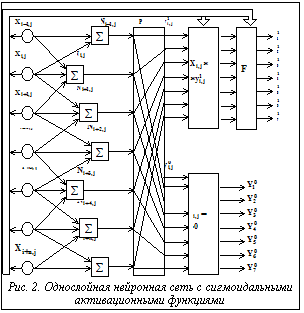 Сигнал от каждого пиксела Xi,j исходного изображения поступает на соответствующий ему нейрон Ni,j, число которых равно числу пикселей. Параллельно с сигналом от пиксела Xi,j на нейрон Ni,j подаются значения соседних пикселей Xi ± 1, j ± 1 (рис.1).
Сигнал от каждого пиксела Xi,j исходного изображения поступает на соответствующий ему нейрон Ni,j, число которых равно числу пикселей. Параллельно с сигналом от пиксела Xi,j на нейрон Ni,j подаются значения соседних пикселей Xi ± 1, j ± 1 (рис.1).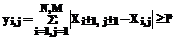 , (1)
, (1) элементов матриц. В остальных случаях, когда пороговая функция не «срабатывает», на выход сети поступают нулевые сигналы
элементов матриц. В остальных случаях, когда пороговая функция не «срабатывает», на выход сети поступают нулевые сигналы  элементов матриц, не являющихся граничными.
элементов матриц, не являющихся граничными. поступают на вход активационного блока F, где преобразуются сигмоидальной функцией передачи, которая математически выражается [5]:
поступают на вход активационного блока F, где преобразуются сигмоидальной функцией передачи, которая математически выражается [5]: . (2)
. (2) Из рисунке 3а и 3б видно, что все точки фона, находящиеся внутри односвязных контуров, удалены. Оставлены лишь точки, принадлежащие границам раздела объектов и фона. Однако вместе с этим имеют место такие недостатки, как искусственное повышение уровня шумов (на 7-10 %), заметное увеличение толщины замкнутых и одиночных линий (до 100 %), то есть происходит искажение исходной полутоновой матрицы.
Из рисунке 3а и 3б видно, что все точки фона, находящиеся внутри односвязных контуров, удалены. Оставлены лишь точки, принадлежащие границам раздела объектов и фона. Однако вместе с этим имеют место такие недостатки, как искусственное повышение уровня шумов (на 7-10 %), заметное увеличение толщины замкнутых и одиночных линий (до 100 %), то есть происходит искажение исходной полутоновой матрицы. Из рисунка 4а видно, что по сравнению с цифровым алгоритмом определения границ нейросетевой увеличивает уровень зашумленности всего на 3-5 %. При этом толщина контурных линий также увеличивается (до 100%). На рисунке 4б представлены результаты обработки исходной полутоновой матрицы нейронной сетью с сигмоидальной активационной функцией передачи, показанной на рисунке 2. Сравнивая исходную полутоновую матрицу (рис. 3а) с полученной нелинейной нейронной сетью (рис. 4б), можно сделать вывод о том, что в данном случае имеет место уменьшение общего уровня зашумленности изображения (на 5-8 %), искажений в толщине контурных линий не происходит. Это объясняется нелинейным характером нейронных активационных функций.
Из рисунка 4а видно, что по сравнению с цифровым алгоритмом определения границ нейросетевой увеличивает уровень зашумленности всего на 3-5 %. При этом толщина контурных линий также увеличивается (до 100%). На рисунке 4б представлены результаты обработки исходной полутоновой матрицы нейронной сетью с сигмоидальной активационной функцией передачи, показанной на рисунке 2. Сравнивая исходную полутоновую матрицу (рис. 3а) с полученной нелинейной нейронной сетью (рис. 4б), можно сделать вывод о том, что в данном случае имеет место уменьшение общего уровня зашумленности изображения (на 5-8 %), искажений в толщине контурных линий не происходит. Это объясняется нелинейным характером нейронных активационных функций.