Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Макроэкономическая балансовая модель для стран с элементами переходной экономики
Аннотация:
Abstract:
| Авторы: Масюков В.А. () - , Матылина Л.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15688 |
Версия для печати Выпуск в формате PDF (1.36Мб) |
В последние годы возникла потребность в более корректном прогнозе макроэкономического развития России с учетом элементов переходной экономики [1-4]. Для достижения этой цели при моделировании макроэкономических процессов необходимо учитывать уровни инфляции внутри страны и за рубежом, влияния продажи нефти на величину валового внутреннего продукта (ВВП), а также характер воздействия этих факторов на сбалансированность товарного и денежного рынков и на соблюдение внешнеэкономического баланса [5-7]. Кроме того, необходимо учитывать уровень доверия населения к действиям правительства и банковской системы [1,2,8]. Решение проблемы корректного макроэкономического прогнозирования зависит также от степени учета неопределенностей, связанных, прежде всего, с оценкой величин притока и оттока капиталов, а также величины утечки капитала за рубеж в зависимости от роста уровня инфляции и изменения цен на нефть [2,8]. Как минимум, требуется установление аналитических зависимостей влияния перечисленных факторов на показатели эффективности экономического развития. Кроме того, рассчитывать на максимизацию величины ВВП без нахождения оптимального соотношения величин выбранных макроэкономических параметров управления представляется весьма сомнительным делом. К сожалению, используемые в настоящее время модели макроэкономического прогнозирования – это в основном модели объяснения, а не оптимизации [5-7]. Оптимизационные макроэкономические модели в настоящее время разрабатываются применительно лишь к попыткам фрагментарного совершенствования экономического механизма страны [9,10]. Таким образом, создание оптимизационной макроэкономической балансовой модели для России с учетом элементов переходной экономики представляет как научный, так и практический интерес. С целью информационной поддержки принятия управленческих решений, обеспечивающих максимизацию ВВП, целесообразна разработка макроэкономической балансовой модели, отвечающей следующим требованиям. 1. Включить в разрабатываемую модель (в отличие от классической балансовой модели Дорнбуша-Фишера [5]) экономические показатели, необходимые для учета ряда особенностей переходной экономики (уровни инфляции внутри страны и за рубежом, реальные процентные ставки внутри страны и за рубежом, величина средней цены на нефть в прогнозируемом периоде, доля продаж нефти в общей величине экспорта, уточненные с использованием перечисленных показателей величины притока и оттока капиталов за рубеж, а также величины утечки капиталов за рубеж). 2. Найти выражение Y0(x,y) для оценки прогнозируемой величины ВВП при условии согласован- ного проведения фискальной и монетарной политики с уточнением входящих в него функциональных зависимостей, которое достигается за счет оптими- зации управляемых параметров (х) (для фиксиро- ванных значений ситуационных параметров (y)) и обеспечивает достижение максимального значения ВВП. 3. Уточнить условие внутреннего экономического баланса [5] для более корректной оценки влияния инвестиций и реального валютного курса: f1(x,y)= =Y1(x,y)–Y2(x,y), где Y1(x,y) – величина ВВП при условии равновесия товарного рынка; Y2(x,y) – величина ВВП при условии равновесия рынка денег. 4. Дополнить условие внешнеэкономического баланса [5] зависимостями, определяющими закономерности притока капитала из-за рубежа и оттока капиталов за рубеж, а также величину утечки капиталов за рубеж: f2(x,y) ≤ 0. 5. Преобразовать общие функциональные зависимости, описывающие экономический кругооборот, для учета конкретных экономических показателей (указанных в п.1 требований) с учетом бездефицитности бюджета f3(x,y)≤0 и с установкой ограничений на управляемые и ситуационные макроэкономические показатели fi(x,y)≤Bi, (N≥i≥4), где N – максимально возможное число ограничений на параметры. Исходя из приведенных требований, макроэкономическая балансовая модель должна осуществлять решение задачи оптимизации выбранных параметров управления, обеспечивающих максимизацию прогнозируемой величины ВВП при выполнении условий внутреннего и внешнего баланса, бездефицитности бюджета и учете ограничений на величины используемых макроэкономических показателей. Указанная задача оптимизации с математической точки зрения представляет собой задачу математического программирования: целевая функция:
условие внутреннего экономического баланса: f1(x,y) = 0, (2) условие внешнего экономического баланса: f2(x,y) ≤ 0, (3) условие бездефицитности бюджета: f3(x,y) ≤ 0, (4) ограничение на управляемые и ситуационные макроэкономические показатели: fi(x,y) ≤ Bi, (N≥i≥4). (5) Сведение задачи макроэкономического моделирования к задаче математического программирования делает возможным использование систем компьютерной математики, что значительно расширяет возможности применения математических методов для решения экономических задач. В зависимости от условий решения экономических задач одни и те же макроэкономические параметры могут выступать в качестве управляемых или ситуационных. Для упрощения изложения метода решения поставленной задачи примем в качестве управляемых параметров величину государственных расходов (G) и величину денежной массы (M), так как эти два параметра являются наиболее подвижными и важными. Общность подхода от этого не страдает, а форма записи сохраняется. Существо метода решения поставленной задачи заключается в дополнении и развитии классической модели Дорнбуша-Фишера [5] для учета влияния элементов переходной экономики и в использовании полученных результатов для описания задачи математического программирования. В связи с тем, что экономические концепции, положенные в основу этого метода, изложены в [8], то представляется возможным ограничиться записью результирующих выражений, полученных для описания целевой функции и ограничений. Естественно, что при упрощающих положениях, когда влияние элементов переходной экономики можно не учитывать, получены выражения классической макроэкономической балансовой модели [5]. Тогда выражение для целевой функции может быть представлено в виде:
где b – фискальный мультипликатор,
g – мультипликатор монетарной политики,
где X(x1,x2) – множество значений параметров управления, удовлетворяющих принятым ограничениям; x1 – государственные расходы (G); x2 – денежная масса (M); y1 – эластичность спроса на деньги по процентной ставке (h); y2 – мультипликатор товарного рынка (aIS),
y3 – уровень цен (
y4 – эластичность инвестиций по процентной ставке (b); y5 – эластичность спроса на деньги по доходу (k); y6 – инвестиции (I);
y7 – автономный спрос (A0); y7 = y28 + y30 + y31 + y32; y8 – предельная склонность к потреблению (c); y9 – трансферты (TR); y10 – величина экспорта при реальном валютном курсе, равном единице (Eex,R=1); y11 – реальный валютный курс с учетом доли продаж нефти в общей величине экспорта (Rn); y11 = y33 × y34+(1-y33) y22; y12 = y30 + y31 + y32; y13 – реальная процентная ставка внутри страны (rr); y14 – сальдо торгового баланса (NX); y15(y35,y36,y37,y38) – приток капитала из-за рубежа (K+); y16(y42,y43) – отток капитала за рубеж (K-); y17 – утечка капитала за рубеж (Fd); y18 – налоговая ставка (T); y19 – максимально возможная величина госрасходов (Gmax); y20(y21,y22) – склонность к импорту (cim);
y21 – предельная склонность к импорту (cim,0); y22(y23,y24,y25) – реальный валютный курс (R);
y23 – обменный валютный курс (E); y24(y23,y26,y27) – величина отношения стоимости потребительской корзины за рубежом к стоимости потребительской корзины внутри страны при известном обменном валютном курсе;
y25(y43,y20,x1,y31,y6,y14) – потребление (C);
y26 – уровень инфляции за рубежом ( y27 – уровень инфляции внутри страны ( y28 – планируемая величина инвестиций (I0); y29 – реальная процентная ставка (rr); y30,y31,y32 – автономный спрос, обусловленный соответственно автономными параметрами потребления (y30), госрасходов (y31) и торгового баланса (y32), иначе: C0, G0, NX0; y33 – доля продаж нефти в общей величине экспорта (Kn); y34 – коэффициент изменения средней цены на нефть относительно планируемой величины (g); y35 – коэффициент доверия к экономической политике правительства; y36(y39,y40,y41) – общая сумма депозитов в банках страны (Dep); y37 – реальная процентная ставка за рубежом ( y38 – коэффициент притока иностранного капитала (K+/D³0) (коэффициент доверия иностранных инвесторов к экономической политике правительства); y39 – коэффициент доверия к банковской системе (0≤KB≤1); y40 – общая величина депозитов при KB = 1 ( y41 – общая величина депозитов при KB = 0 ( y42(y9,y18,y20,y25,y30,y43) – общая величина сбережений населения (S);
y43(x2,y1,y3,y5,y20,y29) – величина импорта (Iim);
Таким образом, общее число параметров описывающих макроэкономическую ситуацию, равно 45. В данном представлении модели 2 из них оптимизируются (x1, x2), а 43 параметра являются ситуационными. В описываемой версии модели все ситуационные параметры разделены на три группы: - исходные данные для моделирования (y7, y8, y9, y10, y12, y13, y19, y21, y23, y24, y26, y27, y28, y29, y30, y31, y32, y33, y34, y36, y37, y40, y41) – всего 23 параметра; - параметры, которые находятся в процессе моделирования (y2, y3, y6, y11, y14, y15, y16, y17, y20, y22, y25, y42, y43) – всего 13 параметров; - параметры, которые находятся на основе тестирования модели по реальным данным исполнения бюджета (y1, y5, y18, y21, y35, y38, y39) – всего 7 параметров. Целевая функция имеет явно выраженный нелинейный характер. При принятых обозначениях и приведенных функциональных зависимостях условие внутреннего экономического баланса (2), являющееся первым ограничением в виде равенства в задаче математического программирования, приобретает вид:
При описании условия внешнеэкономического баланса (3) потребовалось получение эмпирических выражений для оценки величин притока (y15) и оттока капитала (y16), а также величины утечки капитала за рубеж (y17). Эти эмпирические зависимости получены исходя из следующих соображений. В общем случае величина притока капитала (y15) зависит от относительной разности реальных процентных ставок в стране (y13) и за рубежом (y37), а также от степени риска капиталовложений, который отражается в степени доверия зарубежных инвесторов к экономической политике правительства и в степени их интереса к капиталовложениям в нашей стране (y38), и также от экономической активности населения страны, которая выражается общей суммой депозитов в банках страны (y36), величина которых, в свою очередь, зависит от доверия населения к банковской системе. Тогда выражение для прогнозирования величины притока капитала может быть записано следующим образом:
Для проведения моделирования общая сумма депозитов (y36) может быть оценена непосредственно на основе информации от банковской системы или следующей эмпирической зависимости:
Естественно предположить, что величина оттока капитала за рубеж (y16) будет возрастать с падением коэффициента доверия экономической политике правительства, то есть с ростом величины (y35), а также при увеличении превышения величины сбережений населения (y42) над величиной инвестиций (y6), то есть с ростом величины (y42-y6). Тогда выражение для оценки величины оттока капитала за рубеж может быть записано следующим образом:
С учетом предполагаемых закономерностей (11), (13) выражение для условия внешнеэкономического баланса (3) приобретает вид:
Теперь не представляет сложности записать условие бездефицитности бюджета (4) следующим образом:
Для рассматриваемого типа задачи наложим ограничение только на максимально возможную величину госрасходов (x1,max):
Таким образом, получено математическое описание макроэкономической балансовой модели для стран с элементами переходной экономики (формулы 6, 10, 14-16), предназначенной для решения оптимизационных задач макроэкономического прогнозирования, сформулированных как задачи математического программирования. Для проверки работоспособности модели на решении задач макроэкономического прогнозирования разработана программа "Макроэкономическая балансовая модель поддержки управленческих решений по увеличению темпа роста ВВП за счет оптимизации денежной массы". "Модель 1 уровня" позволяет анализировать изменение темпа роста ВВП за счет оптимизации денежный массы при изменении реальной процентной ставки, уровня инфляции, обменного курса и цен на нефть. Модель была оттестирована для исходных данных, приближенных к бюджетам 2000-2002 гг. [11]. Для фактически зарегистрированных уровня инфляции, реальной процентной ставки, обменного курса и цен на нефть для 2000-2002 гг. за счет оптимизации денежной массы потенциальный рост ВВП мог составить 19.7%, 13.1%, 6.9%, больше достигнутого соответственно на 11.5%, 7.6%, 1.5%. При этом оптимальная величина денежной массы за 2000 и 2001 гг. превышает фактическую величину на 12.6% и на 3.4% соответственно, а за 2002 г. фактическая величина превышает оптимальную величину на 18.3%. На основе полученных результатов можно сделать вывод, что эффективность кредитно-денежной политики постепенно повышается. Однако возможности повышения темпов роста ВВП за счет оптимизации денежной массы еще не исчерпаны. В связи с этим определенный интерес представляет создание и использование моделей более высоких уровней, позволяющих увеличить число параметров оптимизации и количество изменяемых параметров, описывающих экономическую ситуацию. Разработанная макроэкономическая балансовая модель для стран с элементами переходной экономики может быть использована для информационной поддержки управленческих решений, направленных на максимизацию величины ВВП за счет оптимизации выбранных параметров управления. Благодаря возможностям изменения макроэкономических показателей в широких пределах (ограниченных только рамками реально допустимых значений), лица, принимающие управленческие решения, имеют возможность проводить исследования для выработки оптимальных вариантов макроэкономического развития. Для дальнейшего расширения возможностей применения этой математической модели целесообразно ее совершенствование на основе введения для пользователей интерактивных режимов общения с использованием специализированных баз данных, а также путем обеспечения возможности проведения исследований на модели через сеть Internet. Список литературы 1. Львов Д. Будущее российской экономики. // Экономист. - 2000. - №12. 2. Стратегия развития государства на период до 2010 года: Доклад, подготовленный рабочей группой Государственного совета РФ под руководством В.И.Ишаева. // Российский экономический журнал. - 2001. - №1. 3. Белоусов А.Р. Эффективный экономический рост в 2001-2010 гг.: условия и ограничения. // Проблемы прогнозирования. - 2001. - №1. 4. Асташов К.И. Социально-экономическое развитие: итоги и перспективы. // Экономист. - 2001. - №9. 5. Дорнбуш Р., Фишер С. Макроэкономика. / Пер. с англ. - М., 1997. 6. Гайгер, Линвуд Т. Макроэкономическая теория и переходная экономика. / Пер. с англ. - М., 1996. 7. Burda M., Wyplosz C. Macroeconomics. Oxford University Press, New York, 1997. 8. Масюков В.А., Масюков В.В. Балансовая модель прогнозирования параметров макроэкономического развития. // Сб. науч. тр.: Теоретические проблемы управления производством и капиталом. - Тверь: МЭСИ. - 2001. 9. Багриновский К.А., Бендиков М.А., Хрусталев Е.Ю. Современные методы управления технологическим развитием. - М.: РОССПЭН, 2001. 10. Катулев А.Н., Колесник Г.В. Программный комплекс оптимизации основных показателей развития отраслей промышленности. // Программные продукты и системы. -1997. - № 2. 11. Российский статистический ежегодник: [Сборник]. - М.: Госкомстат России, 2001. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=641&like=1&page=article |
Версия для печати Выпуск в формате PDF (1.36Мб) |
| Статья опубликована в выпуске журнала № 2 за 2003 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Исследовательское проектирование в кораблестроении на основе гибридных экспертных систем
- Инструментальные и программные средства построения сетевых моделей
- Информационная система оптимизации расписания доставки грузов от производителей сырья
- Правила построения автоматизированных информационных систем экспертной оценки и согласования
Назад, к списку статей



 , (1)
, (1) (6)
(6) , (7)
, (7) ,(8)
,(8) (9)
(9)
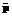 );
);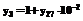 ;
; ;
; ;
;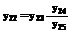 ;
; ;
; ;
; );
); );
);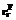 );
); );
);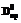 );
); ;
; .
. (10)
(10)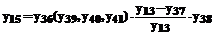 . (11)
. (11) . (12)
. (12)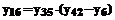 . (13)
. (13) (14)
(14) (15)
(15)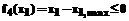 . (16)
. (16)