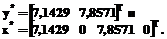Трансформационный подход к решению задач линейного программирования: алгоритмическое и программное обеспечение
| Демидов Н.Е. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Предлагается трансформационный подход для решения оптимизационных задач с линейными ограничениями. Использование параметризованных преобразований, теории двойственности и ряда эвристических процедур позволило значительно уменьшить вычислительную сложность оптимизационных задач с большим числом переменных и ограничений, характерных для современных приложений. Научно-технический прогресс привел к использованию в аналитической деятельности новых информационных технологий. Современные экспертно-аналитические подразделения и службы предприятий и организаций получили инструментарий для автоматизированного решения многих задач, в том числе и оптимизационных (планирование производства и перевозок; управление поставками, запасами и сбытом; инвестиционное проектирование; ценообразование и др.) [1]. Характерными особенностями большинства перечисленных оптимизационных задач является их линейность (различные постановки задач линейного программирования) или наличие при нелинейной целевой функции только линейных ограничений в форме равенств и неравенств, а также высокая размерность (сотни, тысячи и десятки тысяч переменных) и, как следствие, значительные вычислительные затраты на получение решений. В связи с этим представляются актуальными многочисленные исследования, направленные на уменьшение вычислительной сложности указанных задач [2]. Для рассматриваемого класса оптимизационных задач особый интерес представляют методы уменьшения размерности (редукции), основанные на линейно-алгебраических преобразованиях (трансформации) матриц ограничений математических моделей. Предлагаемый ниже трансформационный подход к таким задачам позволяет кардинально уменьшить вычислительные затраты на их решение. Теоретическое обоснование подхода Во многих задачах математического программирования (линейное и квадратичное программирование, нелинейная условная оптимизация и др.) используются так называемые обобщенные обратные (псевдообратные, квазиобратные) матрицы (ООМ) [3]. В задачах оптимизации в большинстве случаев ООМ необходимы для решения систем линейных алгебраических уравнений (СЛАУ) вида AX=b с прямоугольной матрицей A размера n на m (nk) строчного ранга (k=rank A). В настоящее время для расчета основных типов ООМ, и в первую очередь ООМ Мура-Пенроуза [3], имеются детально теоретически обоснованные надежные вычислительные алгоритмы и высокоэффективные программные модули, их реализующие. Известное соотношение для получения общего решения СЛАУ [3]
связывает исходную матрицу A, ее конкретную ООМ A+ и частное решение X0=A+B со свободными параметрами в виде матрицы Y того же размера, что и X. В практических задачах возникает проблема использования минимального числа свободных параметров, то есть проблема минимальной параметризации X, в частности, для уменьшения вычислительной сложности алгоритмов. Минимальные и аппроксимирующие параметризации ООМ и решений СЛАУ открывают также и новые возможности решения многих задач [4]. В этой связи представляется актуальной разработка минимальных параметризированных представлений общих решений СЛАУ и их использование для модификации существующих и создания новых алгоритмов решения оптимизационных задач. Примем без потери общности, что матрица A имеет следующее блочное представление:
в котором подматрица A11 порядка k имеет полный ранг. В случае необходимости такое представление должно быть получено путем перестановок строк и столбцов исходной матрицы и соответствующими преобразованиями математической модели. В качестве A+ необходимо использовать рефлексивную {1,2}–ООМ [4] для A вида
В этом случае минимальное параметризованное общее решение X=X0+SP включает матрицу P свободных параметров и матрицу S вида
подматрица Em-k которой является единичной матрицей порядка m-k. Задачи линейного программирования (ЗЛП) имеют огромное практическое значение, чем объясняется большое число исследований, связанных с ЗЛП. Наиболее известным методом решения ЗЛП является симплекс-метод (СМ), однако для него при решении ЗЛП повышенной размерности (100 – 200 и более переменных) выявлен ряд специфических недостатков (недостаточная численная устойчивость, сложность средств устранения плохо обусловленных базисов и др.). В связи с этими недостатками СМ модифицируются существующие (например итерационные) и разрабатываются новые (в том числе приложения методов нелинейного программирования и, в частности, известный полиномиальный алгоритм Кармаркара) методы решения ЗЛП [5]. Известны прямые методы решения ЗЛП специального типа с помощью ООМ и общих решений СЛАУ [3], однако существенным ограничением предлагаемого подхода является требование линейной независимости строк матрицы A, то есть наличие полного строчного ранга (m>n и k=n). Новые возможности решения подобных задач с использованием минимальной параметризации вида X=X0+SP рассматриваются на примере ЗЛП следующего типа:
Предлагаемый метод минимальной параметризации для решения данной ЗЛП включает следующие этапы. 1. Получение общего решения СЛАУ Ax=b вида x=x0+Bp. 2. Формирование вспомогательной ЗЛП вида
путем редукции исходной ЗЛП с учетом соотношений cTx=cTx0+cTBp, dT=cTB и исключения из критерия оптимизации постоянной составляющей cTx0. 3. Решение редуцированной ЗЛП с помощью хорошо известных алгоритмов поиска набора активных ограничений (НАО
с плотно заполненной матрицей F и последующее определение оптимального решения p* вспомогательной СЛАУ Gp=q, в которой матрица G порядка k-полного ранга и формируется из строк НАО, а вектор q из соответствующих элементов векторов – ограничений zl или zh. 4. Формирование оптимального решения исходной ЗЛП x*=x0+Bp*. Примеры решения ЗЛП Для решения рассматриваемой ЗЛП с двусторонними ограничениями в [6] использован численный метод оптимизации для многошаговых процессов с дискретным управлением. Расчеты производились для следующего примера ЗЛП:
За пять итераций вычислений по используемому в [6] алгоритму получено значение критерия оптимальности cTx= –5,342 при оптимальном значении –4,0435 (ошибка равняется 13,21%). С учетом конкретной структуры и значений элементов матрицы A с помощью предлагаемого подхода найдены
Для определения НАО и получения приближенного решения предлагается решить следующие две вспомогательные оптимизационные задачи. 1. Найти
Решение очевидно:
2. Найти
Решение:
Ошибка в 2,21% для оптимума cTx* = -4,0435 позволяет считать найденное решение приемлемым для большинства практических задач с учетом погрешностей получения исходных данных. Однако дополнительный анализ изменений значений конкретных элементов вектора x при переходе от v* к
при С помощью предложенного подхода для задачи об ассортименте [7] вида
при
исследование ограничения которой
позволило выявить несовместные по знаку условия (строки 2 и 4 матрицы B) и сформировать новую редуцированную ЗЛП с совместными условиями
Преобразованная двойственная ЗЛП имеет вид:
Исследование ограничения
позволило выделить избыточное ограничение – строку 2 в матрице G – и получить оптимальное решение y* редуцированной ЗЛП и соответствующее решение x* исходной ЗЛП
Особенности подхода Принципиальными особенностями предлагаемого подхода являются: 1) понижение размерности исходной ЗЛП с уменьшением числа неизвестных до величины, не превышающей m-k, что может иметь определяющее значение для больших ЗЛП; 2) возможность использования стандартного ПО для выполнения необходимых линейно-алгебраических операций, таких как определение ранга, ортогональных преобразований, разложения по сингулярным числам и др. [4]; 3) возможность применения известных эффективных алгоритмов решения редуцированной ЗЛП, в том числе и предложенных эвристических алгоритмов. Рассматриваемый подход распространяется на задачи интервального ЛП и дробно-линейного программирования. В случае целочисленных задач (о ранце, об ассортименте и др.) описанный подход можно использовать для получения достаточно хороших приближенных решений. Программная реализация ПО для решения ЗЛП на основе трансформационного подхода разработано в инструментальной среде системы для математических расчетов MATLAB версии 6.1 и включает ряд программных систем, и в том числе: версию для разработчиков – с режимом работы в командной строке MATLAB; для конечных пользователей – на основе приложения Excel Link; для учебного назначения – на основе приложения Notebook и для ИТ-специалистов – в виде специализированной библиотеки тулбокса (toolbox) LPT. ПС для режима работы в командной строке MATLAB была использована для проведения сравнительного исследования известных и оригинальных алгоритмов решения проблем ЗЛП и содержит свыше 50 модулей в виде М-функций MATLAB, которые подразделены на три группы (уровня): · базовые модули – не используют вызовов других модулей ПС; · модули второго уровня – предназначены для решения конкретных задач редукции, агрегации и трансформации моделей ЛП, определения внутренних допустимых точек систем линейных ограничений и выполнения процедур предоптимизационного и постоптимизационного анализов; · модули третьего уровня – законченные функциональные приложения для решения ЗЛП в различных постановках, описанных в специальной литературе. Список литературы 1. Филлипс Д.Г., Гарсиа-Диас А. Методы анализа сетей. – М.: Мир, 1984. – 496 с. 2. Гольштейн Е.Г., Немировский А.С., Нестеров Ю.Е. О некоторых последних достижениях в оптимизации // Экономика и математические методы. – 1990. – №1. – С. 178-190. 3. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. - М.: Наука, 1997. – 224 с. 4. Демидов Н.Е. Параметризация обобщенных обратных матриц: алгоритмическое и программное обеспечение // Программные продукты и системы. - 1998. - №2. – С. 33-36. 5. Муртаф Б. Современное линейное программирование. Теория и практика. – М.: Мир, 1984. – 224 с. 6. Основы теории оптимального управления. – М.: Высшая школа, 1990. – 430 с. 7. Вагнер Г. Основы исследования операций. – М.: Мир,1973. – Т.1. – 355 с. |
http://swsys.ru/index.php?id=670&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Анализ российского и зарубежного рынков программных продуктов
- Спецификация объектно-ориентированной модели данных с помощью отношений
- Гибридный нейросетевой алгоритм построения аппроксимационных моделей сложных систем
- Информационная система оптимизации расписания доставки грузов от производителей сырья
- Инструментальные и программные средства построения сетевых моделей



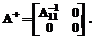
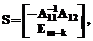
 .
.
 ) для оптимизационных задач с системой ограничений вида
) для оптимизационных задач с системой ограничений вида





 .
.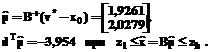

 и степени приближения их к соответствующим элементам zl и zh позволяет выделить НАО (две последние строки матрицы B), сформировать матрицу G и вектор q и рассчитать точный оптимум:
и степени приближения их к соответствующим элементам zl и zh позволяет выделить НАО (две последние строки матрицы B), сформировать матрицу G и вектор q и рассчитать точный оптимум: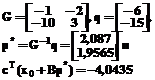

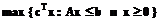

 получена преобразованная ЗЛП
получена преобразованная ЗЛП