Подход к созданию нечетких динамических систем поддержки принятия решений
| Головина Е.Ю. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Одной из важных задач, которую решают разработчики систем поддержки принятия решений (СППР) на начальных этапах их создания, является задача моделирования поведения сложных объектов. Наблюдается резкий рост количества работ, касающихся логического подхода к моделированию поведения сложных объектов. Большой вклад в это научное направление внесли зарубежные логики [1-6]. Российские ученые также вносят свой вклад в создание логических методов моделирования сложных объектов, вершиной работ в котором стала теория семиотического моделирования [7,8], предложенная Д.А. Поспеловым и представляющая математический базис для построения интеллектуальных систем качественно нового уровня. Так, на смену формальной системе и ее частичным модификациям приходит семиотическая система, позволяющая адекватно описывать современные проблемные области с их открытостью, динамичностью, cложноструктурированностью [9-12]. Рассмотрим теорию семиотического моделирования в приложении к интеллектуальным СППР. Построение СППР осуществляется в основном в условиях неточной, неполной, противоречивой, неоднозначной, нечеткой информации, выделяемой при описании реальных объектов управления (ОУ). Сбор статистических данных, описывающих ОУ, представляет длительный процесс или иногда бывает невозможен из-за сложности проведения измерений характеристик ОУ. Поэтому лицо, принимающее решение (ЛПР), при описании своих действий использует качественную информацию. В последние годы разработано огромное число методов моделирования ОУ в условиях дефицита информации [13,14]. Нами выбран подход к моделированию, основанный на нечетких моделях, поскольку СППР, в основе которой лежат нечеткие модели, может быть реализована как программно-аппаратный комплекс. Семиотическое моделирование на базе нечетких логик. Интерпретация семиотической системы в терминах математического аппарата нечетких логик. Определение 1. Семиотическая система есть SS={FS, a(T), b(P), g(A), s(R)}, где FS={T,P,A,R} – формальная система, элементами которой являются: Т – множество термов; P – множество правил построения правильно построенных формул; А – множество аксиом; R – множество правил вывода; a(T), b(P), g(A), s(R) – правила изменения элементов T,P,A,R [8]. В [8] отмечается, что если зафиксировать такты работы семиотической системы, то на каждом из этих тактов она работает как некоторая формальная система. Таким образом, семиотическую систему можно представить в следующем виде: SS={{FSi}, {Àj}}, i=1,n, j=1,m, где {FSi}, i=1,n – множество формальных систем; {Àj}, j=1,m – множество переходов от одной формальной системы к другой. Определение 2. Нечеткая семиотическая система (mSS) есть mSS={mFS,a(T), b(P),g(A),s(R),j(W)}, где mFS={T,P,A,R,W} – нечеткая формальная система; T,P,A,R – элементы FS; W – алгебра (теоретико-множественные операции, основанные на Т-нормах и Т-конормах); a(T), b(P), g(A), s(R) – правила изменения элементов FS; j(W) – правила изменения алгебры (теоретико-множественных операций, основанных на Т-нормах и Т-конормах) [15-17]. Приведем интерпретацию семиотической системы в терминах нечетких логик. Нашей целью является задание семиотической системы на базе нечетких логик в такой нотации, которая стала бы платформой для создания СППР качественно нового уровня, в основе функционирования которых лежит правило вывода – обобщенный Modus Ponens [14]. Определение 3. Семиотическая система (mSS) на базе нечетких логик есть mSS={T,P,A,R,TS,a(T), b(P),g(A),s(R),j(TS)}, где mFS={T,P,A,R,TS} – формальная система, элементами которой являются: T – множество лингвистических переменных; Р – множество правил построения из лингвистических переменных нечетких продукционных правил; А – множество аксиом, описывающих функционирование ОУ и заданных в виде нечетких продукционных правил; R – правило вывода (обобщенный Modus Ponens); TS – множество триангулярных норм (Т-норм и Т-конорм), используемых для «настройки» правила вывода – обобщенного Modus Ponens на специфику ОУ; a(T)*, b(P), g(A) – правила изменения элементов Т, Р, А в mFS; s(R) – правила изменения реализаций обобщенного Modus Ponens, позволяющие отобразить специфику ОУ (общеизвестными являются две реализации обобщенного Modus Ponens – алгоритмы Сугено и Мамдани); j(TS) – правила изменения триангулярных норм, позволяющие также отобразить специфику ОУ. Далее определим семиотическую систему на базе нечетких логик через множество формальных систем и переходов между ними. Определение 4. Семиотическая система (mSS) на базе нечетких логик есть mSS={{mFSi},{Àj}}, i=1,n; j=1,m, где {mFSi}, i=1,n – множество формальных систем, mFSi ={T,P,A,R,TS}; {Àj}, j=1,m – множество переходов между формальными системами. Определение 5 (является модификацией определения 4). Семиотическая система (mSS’) на базе нечетких логик есть mSS’={{mSsi},{Àj}}, i=1,n; j=1,m, где mSsi={mFSi, j’(TS)} – расширенная формальная система, в которой mFSi ={T,P,A,R,TS} – формальная система; j’(TS): TS ®TS’, где TS’ÍTS – функция, задающая изменение триангулярных норм в формальной системе mFSi (или функция, задающая очередность применения триангулярных норм в обобщенном Modus Ponens в формальной системе mFSi); {Àj}, j=1,m – множество переходов между расширенными формальными системами; n – число расширенных формальных систем; m – число переходов между расширенными формальными системами. Реализация семиотической системы на базе нечетких логик Семиотическая модель есть SM={S, R1 , …, Rn}, в которой S – множество объектов и Ri , i=1,n – отношение являются изменяемыми [8]. Реализация семиотической модели осуществляется за счет операции моделирования, то есть приписывания конкретных имен и характеристик объектам модели и конкретных имен отношениям модели. Таким образом, имеем следующее определение.
Дальнейшим развитием работы [8] является описание свойств отношения перехода между моделями подобно заданию свойств отношения достижимости между мирами в модели Крипке [23,24]. Далее под семиотической системой будем понимать реализацию семиотической системы на базе нечетких логик. Рассмотрим способы задания отношения перехода между моделями. Задание отношения перехода между моделями в виде куба переходов
От одной модели возможны переходы к нескольким. Модели могут создаваться и удаляться в процессе моделирования при обновлении знаний об ОУ. В системе управления некоторым реальным объектом или процессом траектория движения от одной модели к другой должна оставаться непрерывной. Это достигается за счет того, что, когда завершается процесс моделирования ОУ на основе данной модели, ОУ находится в состоянии, которое становится первым для последующей модели [8]. Поступление новой информации от ОУ или увеличение знаний об ОУ, изменение конечного состояния (целевой ситуации), а также поступление специальных сигналов от ОУ, свидетельствующих об изменении внешних воздействий на него, может привести к потребности смены модели управления. Поскольку в момент поступления такой информации функционирование ОУ моделируется на основе модели с фиксированной парой , переход определяется парой моделей, одна из которых является сменяемой, другая – той, на которую она сменяется, с приписанными к ним парами, задающими Т-номы и Т-конормы. Переходы между моделями могут быть заданы и матрицей переходов между моделями (рис. 2). На пересечении строки и столбца ставится «крест», если возможен переход из mSsк в mSsр при выполнении максиминной операции, определенной парой , которая сменяется на максиминную операцию, заданную парой в mSsр. Задание отношения перехода между моделями в виде метаправил При моделировании управления сложным объектом отношение перехода между моделями может задано метаправилами*, использующимися для задания смены моделей управления, которая может быть необходима при изменении конечного состояния (целевой ситуации или цели) при его достижении ОУ, а также при декомпозиции сложной модели управления на более простые. Метаправила имеют вид: [<модельi >:] [<состояниеj >] IF <условие> THEN <модельк >, где <модельi > и <состояниеj > используются для ограничения области действия метаправила; <модельк > является моделью, на которую меняется <модельi >. При этом должен быть выполнен принцип непрерывного управления, то есть состояниеj моделиi является первым для моделик. Условиями являются: внешнее неуправляемое воздействие (возмущение); внешнее управляемое воздействие (команда ЛПР); логическая формула, задающая ограничения на входные и выходные переменные моделиi.
Рассмотрим прототип нечетких семиотических систем ППР (НССППР) по управлению движением автомобиля в лабиринте (созданный совместно со студентами кафедры прикладной математики Московского энергетического института (технического университета) А. Рудь, А. Чеховым, Е. Максимовой, М. Серебренниковой). Ограничимся лабиринтом произвольной формы, но состоящим из прямых стен. Положим, что при движении автомобиля по лабиринту покрытие может меняться с асфальтированного на песчаное, и лабиринт может состоять из прямых стен, расположенных под углом 90°, а также под произвольными углами. Данные ситуации влияют на управление движением автомобиля. Отсюда возникает 4 возможных ситуации (в нашем случае 4 нечеткие модели ОУ), представленные в таблице. Рассмотрим для примера подробно модель 1. Для движения автомобиля по лабиринту определены следующие входные переменные: 1. Alpha_Input – угол обзора; диапазон значений – 0°– 60°. Значения, принимаемые этой переменной – very_large, large, medium, small. 2. Left_Angle – угол между продолжением левого луча угла обзора и препятствием; диапазон значений – 0°– 180°. Значения, принимаемые этой переменной – left1, left2, left3, left4 по возрастанию. 3. Right_Angle – угол между продолжением правого луча угла обзора и препятствием; диапазон значений – 0°– 180°. Значения, принимаемые этой переменной – right1, right2, right3, right4 по возрастанию. 4. Distance – дистанция до препятствия; диапазон значений – 0–20 единиц. Значения, принимаемые этой переменной – near, small, medium, far, very_far. Иллюстрация входных лингвистических переменных приведена на рисунке 3. Выходные переменные: 1. Angle – угол отклонения от текущего направления; диапазон значений от –180° до 180°. Значения, принимаемые этой переменной – left4, left3, left2, left1, center, right1, right2, right3, right4. 2. Speed – скорость движения автомобиля по лабиринту; диапазон значений от 0 до 10 единиц. Значения, принимаемые этой переменной – very_slow, slow, medium, fast, very_fast. 3. Alpha – выходной угол обзора (используется для пересчета значений Alpha_Input); диапазон значений 0°– 60°. Значения, принимаемые этой переменной – very_large, large, medium, small.
Опишем принципы работы данной нечеткой модели. Если расстояние до препятствия больше максимального значения дистанции (>20), то автомобиль едет по своему направлению с максимально возможной скоростью. Как только в поле его видимости (оно определяется наибольшим размером дистанции) попадает стена, то автомобиль сбрасывает скорость и расширяет угол обхвата. Стоит отметить, что значение переменной Alpha_Input уменьшается, что влечет за собой увеличение угла обхвата. Вычисляются значения Left_Angle и Right_Angle, и осуществляется поворот в сторону острого угла. Если значения Left_Angle и Right_Angle совпадают, то поворот осуществляется налево на малый угол. Изложенные действия описаны определенными правилами, например: 1. IF leftangle IS left1 AND (rightangle IS right2 OR rightangle IS right3 OR rightangle IS right4) THEN angle IS left1 2. IF leftangle IS left2 AND (rightangle IS right3 OR rightangle IS right4) THEN angle IS left2 3. IF leftangle IS left3 AND rightangle IS right4 THEN angle IS left3. Следует отметить тот факт, что существуют и косвенные переменные, отвечающие за состояние автомобиля и не использующиеся в системе WARP-SDT. Например, текущие координаты автомобиля, направление движения автомобиля на данный момент (это угол отклонения вектора направления движения от оси Х по часовой стрелке). Данные переменные влияют на пересчет входных значений по выходным. Предположим, что теперь форма стен лабиринта строго 90°, а покрытие осталось тем же, асфальтовым (2-я нечеткая модель ОУ). На рисунке 5 представлены изменения выходной переменной Angle (ее значения будут соответственно left, center, right).
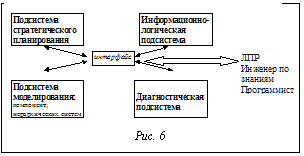
Таким образом, разработанная семиотическая модель, положенная в основу НССППР по управлению движением автомобиля по лабиринту, состоит из 92 продукционных правил. Настройка нечетких моделей управления на Т-нормы и изменение их при возникновении управляемых и неуправляемых воздействий на ОУ позволяет оптимизировать нечеткие модели управления (то есть повысить эффективность управляющих воздействий на ОУ). Данный эксперимент показал, что построение НССППР на основе предложенного логико-семиотического аппарата, повышает качество принимаемых решений. Оценка эффективности осуществляется на качественном уровне на основе визуализации моделирования поведения ОУ в прототипе НССППР по управлению движением автомобиля в лабиринте. Интегрированное инструментальное средство Trincon V.9.0 Разработано несколько версий инструментального средства для создания нечетких систем управления Trincon (Triangular Norms Controller), из которых каждая последующая версия является расширением функциональных возможностей предыдущей [25-28]. Инструментальное средство Trincon v.9.0, разработано в конце 1999 г. [29-36]. В нем реализована возможность настройки композиционного правила вывода на следующие Т-нормы и Т-конормы [14]: Þ Т-норма и Т-конорма Заде: T1(x, y) = min(x, y), S1(x, y) = max(x, y); Þ вероятностные Т-норма и Т-конорма: T2(x, y) = x · y, S2(x, y) = x + y - x · y; Þ Т-норма и Т-конорма Лукасевича: T3(x, y) = max(0, x + y-1), S3(x,y) = min(1,x + y); Þ Т-норма и Т-конорма Франка: p>0 T4(x,y)=logp S4(x,y)=1-logp Þ Т-норма и Т-конорма Сугено: s³-1 T5(x,y)=max[0,x+y-1-s*(1-x)*(1-y)], S5(x,y)=min[1,x+y+s*x*y], а также на гибридные Т-нормы [15-17]. Компонентами инструментального средства Trincon v.9.0 являются: подсистема вывода, в основе которой лежит правило вывода – обобщенный Modus Ponens, – настраиваемое на Т-нормы и Т-конормы; подсистема загрузки исходных данных**, которыми являются лингвистические переменные [21,22], их значения описываются функциями принадлежности, и нечеткие продукционные правила, а также исходные тесты; подсистема сохранения результатов функционирования нечеткой системы управления, разрабатываемой в Trincon; подсистема настройки вывода на гибридные Т-нормы [15-17]; подсистема визуализации функционирования нечеткой системы управления с поддержкой 2D- и 3D-графиков; подсистема динамического изменения Т-норм; подсистема поддержки семиотического моделирования на базе нечетких логик; информационно-управляющая система, обеспечивающая ЛПР недостающей информацией для принятия решений; подсистема поддержки многозадачности; подсистема помощи. Инструментальное средство SETRIAN В 2000 г. начата разработка инструментального средства SETRIAN (Semiotic Tool on Triangular Norms) для создания нечетких динамических СППР [39,40]. Основными компонентами инструментального средства SETRIAN являются следующие. · Подсистема моделирования ОУ, основным назначением которой является: моделирование процесса управления объектом в условиях дефицита информации, то есть на основе качественной информации, используемой ЛПР для описания своей деятельности; моделирование процесса управления многорежимными ОУ; стыковка моделей управления подсистем ОУ, имеющих информационные связи, то есть последнее состояние предыдущей подсистемы является начальной для последующей. · Подсистема стратегического планирования, служащая для: задания начального и конечного состояний ОУ; планирования путей достижения конечного состояния ОУ; выбора наилучшего пути достижения конечного состояния ОУ. (В качестве конечного состояния ОУ может выступать цель, которую ОУ должен достигнуть. Таким образом, в данной подсистеме планируются пути достижения цели ОУ, а также осуществляется выбор наилучшего пути достижения цели ОУ). · Информационно-логическая подсистема, используемая для задания онтологии проблемной области (объектов, отношений, аксиоматики), а также для определения структуры ОУ, сведений о режимах функционирования ОУ и т.п. (Описанная структура ОУ используется при создании иерархических систем управления). · Диагностическая подсистема, объясняющая причины возникновения внештатных ситуаций на ОУ и осуществляющая контроль последствий принятых решений в процессе моделирования динамического ОУ. Архитектура инструментального средства SETRIAN представлена на рисунке 6.
Параллельно с подсистемой моделирования осуществляется разработка диагностической подсистемы и подсистемы стратегического планирования. Информационно-логическая подсистема, в основе которой лежат механизмы вывода в многоуровневой логике [42-45], интегрирована с подсистемой моделирования в инструментальном средстве SETRIAN. Диагностическая подсистема позволяет выявить наиболее возможные причины возникновения внештатных ситуаций на ОУ и осуществить контроль последствий принятых решений в процессе моделирования динамического ОУ. В основе этой подсистемы лежит оригинальный алгоритм вероятностных абдуктивных рассуждений для сложноструктурированных ОУ. Разработанный алгоритм базируется на [46,47]. В основе подсистемы стратегического планирования лежит разработанный математический аппарат, приведенный в [48]. Разработанный математический аппарат поиска лучшего пути достижения конечного состояния ОУ базируется на алгоритмах, созданных Н. Нильсоном [49]. Список литературы 1. McCarthy J. Situations, Actions and Causal Laws // Stanford Artificial Intelligence Project: Memo 2, 1963. 2. McCarthy J., Hayes P.J. Some Philosophical Problems from the Standpoint of Artificial Intelligence// In D. Michie (ed), Machine Intelligence 4, American Elsevier, New York, NY, 1969. 3. McCarthy J. Situation Calculus with Concurrent Events and Narrative// www.stanfornd.edu/u/jmc/e93/narrative, April, 2000. 4. Levesque H., Pirril F., Reiter R. Foundations for the Situation Calculus// Linkoping Electronic Articles in Computer and Information Science,1998, Vol. 3 5. Reiter R. Knowledge in Action: Logical Foundations for Describing and Emplementing Dynamical Systems//http://www.cs. toronto.edu/~cogrobo, 1999. 6. Miller R., Shanahan M. The Event Calculus in Classical Logic – Alternative Axiomatisations. Linkoping// Electronic Articles in Computer and Information Science. 1999 ,Vol. 4. 7. Pospelov D.A. Situation Control, an Overview. Proceedings of Workshop on Russian Situation Control and Cybenetic //Semiotic modeling. Editor R.J,. Strohl. Battelle Columbus Ohio, USA,1996. 8. Поспелов Д.А., Осипов Г.С. Прикладная cемиотика// Новости ИИ. - 1999. - №1. 9. Поспелов Д.А. Логико-лингвистические модели в системах управления. - М.: Экономика,1981. 10.Поспелов Д.А. Ситуационное управление: Теория и практика. -М.: Наука, 1986. 11.Мартынов В.В. Семиотические основы информатики.-Мн.: Наука и техника, 1974. 12.Клыков Ю.И. Семиотические основы ситуационного управления. - Изд-во МИФИ, 1974. 13.Рыков А.С. Методы системного анализа: многокритериальная и нечеткая оптимизация, моделирование и экспертные оценки. - М.: Экономика, 1999. 14.Нечеткие множества в моделях управления и искусственного интеллекта. // Под ред. Д.А. Поспелова - М.: Наука,1986. 15.Averkin A.N. Decision Making Based on Multivalued Logic and Fuzzy Logic. Architectures for Semiotic Modeling and Situation Analysis in Large Complex Systems //Proceedings of the 1995 ISIC Workshop, 27-29 August, Monterey, California, 1995. 16.Averkin A.N,.Pospelov D.A., Tarasov A Managing Linguistically “Soft Computing, Concurrent Engineering, What Else?// Proceedings of the Sixth International Fuzzy Systems Association World Congress, edited by V.B Verdaguer, San Paulo, Brazil, July 22-28, 1995, Vol. 2. 17.Averkin A. N.“Fuzzy Logics Simulation Technology in General Strategy of Intelligent System Designing//Proceedings of the Second International Conference on Application of Fuzzy Systems and Soft Computing, edited by R.A.Aliev, K.W.Bonfig, F.Aliev, F.Wieland, ICAFS’96, Siegen, Germany – June 25-27, 1996. 18.Klement E.P. Construction of fuzzy s-algebras using triangular norms// J. Math. Anal. Appl., 1994,vol. 8 , pp.1001-1023. 19.Batyrshin I., Kaynak O. Parametric Classes of Generalized Conjunction and Disjunction Operations for Fuzzy Modeling. // IEEE Transactions on Fuzzy Systems, 1999, vol. 7, No.5, pp. 586-596. 20.Batyrshin I. Generalized Parametric Conjunction Operations in Fuzzy Modeling // Fuzzy Control. Theory and Practice. R. Hampel, M. Wagenknecht, N. Chaker (Eds.).- Physica-Verlag. A Springer-Verlag Company, 1999, pp.89-97. 21.Zadeh L.A. Fuzzy sets//Inform.&Control, 8, 1965, pp. 338-353. 22.Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений /Пер. с англ..-М.: Мир, 1976. 23.Kripke S. Semantical considerations on modal logic // Oxford University Press, London,1971. /Пер. в сб.: Семантика модальных и интенсиональных логик. – М.: Прогресс, 1981. с. 27-40. 24.Логический подход к искусственному интеллекту: От модальной логике к логике баз данных /Пер. с франц. Тейз А., Грибомон П., Юлен Г. и др. - М.: Мир, 1998. 25.Аверкин А.Н., Головина Е.Ю., Сергиевский А.Е. Проектирование нечетких регуляторов на основе триангулярных норм // Изв. РАН. Теория и системы управления, 1997.- № 5. 26.Аверкин А.Н., Головина Е.Ю., Круг П.Г. Система настройки модели нечеткого регулятора на логику пользователя// Тр. VI-й нац. конф. с междунар. участием (КИИ-98). - Пущино. -ОНТИ. ИФПБ РАН, 1998. - т. 1. 27.Аверкин А.Н., Головина Е.Ю. Программное средство создания нечетких семиотических моделей управления // Тр. 4-го междунар. сем. по прикладной семиотике, семиотическому и интеллектуальному управлению ASC/IC’99. - М., ПАИМС, 1999. 28.Аверкин А.Н., Головина Е.Ю. Нечеткая семиотическая система управления. Интеллектуальное управление: новые интеллектуальные технологии в задачах управления (ICIT’99) // Тр. междунар. конф. (Переславль-Залесский).- М.: Физматлит, 1999. 29.Golovina E. The Tool of Fuzzy Semiotic Models Designing for Decision Making Support System // 14-th European Conference on Artificial Intelligence (ECAI), Workshop Notes, Berlin, August, 2000, рр. 44-49. 30.Головина Е.Ю. Программное средство моделирования управления на основе математического аппарата прикладной семиотики // Тр. междунар. конф.: Идентификация систем и задачи управления (SICPRO’2000) (Москва, 26-28 сентября 2000 г.) -Компакт-диск ISBN 5-201-09605-0, 11 с. 31.Головина Е.Ю. Использование интегрированного инструментального средства создания нечетких динамических систем поддержки принятия решений в учебном процессе // Междунар. форум информатизации-2000: Докл. междунар. конф.: Информационные средства и технологии (17-19 октября 2000 г.) В 3 т. Т. 2.- М.: Изд-во "Станкин", 2000.- С. 172-175. 32.Головина Е.Ю. Интегрированное инструментальное средство для создания нечетких динамических систем поддержки принятия решений // Тр. 7-й нац. конф. по искусственному интеллекту с междунар. участием. - М.: Изд-во. Физ-матлит, 2000.- Т. 2. - С.448-456. 33.Averkin A.N., Golovina E.Y. Tool for Designed fuzzy Semiotic Control Models.// Proceedings of Fourth International Conference on Application of Fuzzy Systems and Soft Computing (ICAFS’2000), Siegen, Germany, June, 2000, pp. 111-116. 34.Golovina E. Y.. The Tool of Fuzzy Dynamic Decision Making Support System Designing// Proceedings of the 2nd International Workshop on Computer Science and Information Technologies, CSIT2000, Ufa, Russia, September 18-23, 2000, pp. 374-380. 35.Головина Е.Ю. Нечеткая семиотическая система поддержки принятия решений // Изв. РАН. Теория и системы управления.-2000. - № 6. - С. 126-133. 36.Golovina E.Yu. A fuzzy Semiotic System for Decision Support// Journal of Computer and System Sciences International,2000, Vol.39, No.6 (МАИК НАУКА/Interperiodica Publishing), рр.958-964. 37.Pagni A., Poluzzi R., Rizzotto G.G.WARP: Weight Associative Rule Processor. An Innovative Fuzzy Logic Controller// IIZUKA’92-2ND International Conference on Fuzzy Logic and Neural Networks, 1992. 38.Watanabe H., Dettloff W.M., Yount K.E. A VLSI Fuzzy Logic controller with Reconfigurable Cascadble Architecture// IEEE Journal of solid-state circuits,1990, Vol. 25, No 2. 39.Головина Е.Ю. Архитектура инструментального средства для создания динамических нечетких систем поддержки принятия решений // Науч. сессия МИФИ-2001. - Сб. науч. тр. в 14 т. - Т.3. Банки данных. Интеллектуальные системы. Программное обеспечение. - М.: МИФИ, 2001. - С. 90-91. 40.Головина Е.Ю. Метод создания нечетких динамических систем поддержки принятия решений// Компьютерная хроника. - ООО «ИНТЕРСОЦИОИНФОРМ», 2001. - № 2, С. 37-51. 41.Головина Е.Ю. Метод построения интеллектуальных адаптивных систем управления на основе отношения перехода между моделями. РАН. Автоматика и телемеханика. - М.: Наука. - 2001. - № 10. - С. 65-77. 42.Ohsuga S., Yamauchi H. Multi-layer logic - a predicate logic including data structure as knowledge representation language// New generation computing,1985, Vol.3,-№.4. 43.Ohsuga S. Toward intelligent CAD systems//Computer Aided Design, 1989, Vol.21, No.5. 44.Vagin V.N., Viktorova N.P., Golovina E.Yu. Multi-layer Logic as a Knowledge Representation Model in the CASE System.//Journal of Computer and Systems Sciencis International. 1995, Vol. 33, No.3. 45.Вагин В.Н., Головина Е.Ю., Оськин Ф.Ф. Модели и методы представления знаний в CASE-технологии.- Интеллектуальные системы.- Т.2. Вып.1-4.-М.: Издат. центр РГГУ, 1997. 46.Console L., Theseider D. Choices in abductive reasoning with abstraction axioms. 47.Poole D. Probabilistic Horn abduction and Bayesian networks. Artificial Intelligence 64, 1993, 81-129. 48.Головина Е.Ю., Пименов М.А. Интеллектуальное средство поддержки деятельности аналитика// Сб. докл. междунар. конф. по мягким вычислениям и измерениям (SCM'99). - СПб, май, 1999. - Т. 2. - С.102-104. 49.Нильсон Н. Искусственный интеллект. Методы поиска и решений. - М.: Мир, 1973.- 270 с. |
http://swsys.ru/index.php?id=683&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- Средства обеспечения надежности функционирования информационных систем
- Опыт разработки и эксплуатации системы управления базами данных (DBS/R)
- Гибридный нейросетевой алгоритм построения аппроксимационных моделей сложных систем
- ДИНАМИКА-2 - программа для решения осесимметричных и плоских задач

 Определение 6. Реализация семиотической модели на базе нечетких логик есть SMR={M,R}, где M={M1 , …, Mn}, Mi, i=1,n – прикладная модель ОУ, описывающая состояние ОУ, для задания которой используется mSsi; R – отношение перехода между моделями (RÍM*M).
Определение 6. Реализация семиотической модели на базе нечетких логик есть SMR={M,R}, где M={M1 , …, Mn}, Mi, i=1,n – прикладная модель ОУ, описывающая состояние ОУ, для задания которой используется mSsi; R – отношение перехода между моделями (RÍM*M). Данный способ позволяет адекватно представить в нечеткой СППР динамику изменений состояний ОУ и знания эксперта об ОУ. При этом изменение триангулярных норм в mSs дает возможность адекватно отобразить специфику ОУ. Переходы между моделями представляются в виде направленных дуг, соединяющих точки трехмерного куба, изображенного на рисун- ке 1. Используются следующие обозначения: M={m1, …, mn} – множество моделей, где в основе mi (i=1,n) лежит mSsi; V=V’ÈV’’, где V’={v1’,…, vp’} – множество неуправляемых факторов (возмущений), воздействующих на ОУ; V”={v1”,…, vm”} – множество управляющих воздействий на ОУ (например, принятие решений о переходе на другой режим функционирования); – множество пар = {, …, }, где , i=1,…,z – пара, задающая максиминную операцию, лежащую в основе правила обобщенного Modus Ponens [14].
Данный способ позволяет адекватно представить в нечеткой СППР динамику изменений состояний ОУ и знания эксперта об ОУ. При этом изменение триангулярных норм в mSs дает возможность адекватно отобразить специфику ОУ. Переходы между моделями представляются в виде направленных дуг, соединяющих точки трехмерного куба, изображенного на рисун- ке 1. Используются следующие обозначения: M={m1, …, mn} – множество моделей, где в основе mi (i=1,n) лежит mSsi; V=V’ÈV’’, где V’={v1’,…, vp’} – множество неуправляемых факторов (возмущений), воздействующих на ОУ; V”={v1”,…, vm”} – множество управляющих воздействий на ОУ (например, принятие решений о переходе на другой режим функционирования); – множество пар = {, …, }, где , i=1,…,z – пара, задающая максиминную операцию, лежащую в основе правила обобщенного Modus Ponens [14]. Применимость логико-семиотического аппарата для создания динамических нечетких СППР
Применимость логико-семиотического аппарата для создания динамических нечетких СППР При разработке данной семиотической системы в качестве инструментального средства для создания нечетких моделей ОУ использовалось программное средство WARP-SDT [37,38], разработанное итальянской фирмой SGS-THOMSON и являющееся инструментом для создания моделей нечеткого регулятора. В дальнейшем для создания нечетких моделей ОУ будут также использоваться разрабатываемый редактор функций принадлежности и продукционных правил и программное средство Fuzzy ToolBox системы Matlab 6.0.
При разработке данной семиотической системы в качестве инструментального средства для создания нечетких моделей ОУ использовалось программное средство WARP-SDT [37,38], разработанное итальянской фирмой SGS-THOMSON и являющееся инструментом для создания моделей нечеткого регулятора. В дальнейшем для создания нечетких моделей ОУ будут также использоваться разрабатываемый редактор функций принадлежности и продукционных правил и программное средство Fuzzy ToolBox системы Matlab 6.0. На рисунке 4 в качестве примера приведены функции принадлежности значений выходной переменной Angle. Функции принадлежности остальных переменных строятся аналогичным образом.
На рисунке 4 в качестве примера приведены функции принадлежности значений выходной переменной Angle. Функции принадлежности остальных переменных строятся аналогичным образом.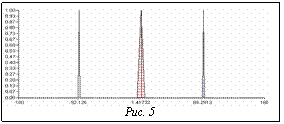 Правила 2-й модели принципиально не отличаются от правил 1-й. Если теперь учесть то, что покрытие лабиринта при произвольной его форме песчаное (3-я модель), то правила претерпевают изменения. Например, правила, вычисляющие скорость в зависимости от дистанции. В данном случае скорость движения будет быстрой не только в случае большой дистанции, но и в случае средней и небольшой, так как продвижение по песку замедляет скорость и, чтобы компенсировать ее потери, выходное значение оставляется большим. Аналогично строится и 4-я модель, учитывающая и песок, и угол между стенками лабиринта, строго равный 90°.
Правила 2-й модели принципиально не отличаются от правил 1-й. Если теперь учесть то, что покрытие лабиринта при произвольной его форме песчаное (3-я модель), то правила претерпевают изменения. Например, правила, вычисляющие скорость в зависимости от дистанции. В данном случае скорость движения будет быстрой не только в случае большой дистанции, но и в случае средней и небольшой, так как продвижение по песку замедляет скорость и, чтобы компенсировать ее потери, выходное значение оставляется большим. Аналогично строится и 4-я модель, учитывающая и песок, и угол между стенками лабиринта, строго равный 90°.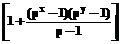 ,
, ;
; Каждая подсистема является многофункциональной компонентой. Последняя версия подсистемы моделирования описана в [41]. Реализация компоненты изменения правила вывода в процессе моделирования ОУ позволит изменять все элементы формальной системы mFS={T,P,A,R,TS} в подсистеме моделирования инструментального средства SETRIAN, поскольку элементы T (термы – лингвистические переменные), P (правила построения правильно построенных формул), A (аксиомы–продукционные правила) изменяются при смене нечетких моделей, TS (триангулярные нормы) изменяются в рамках нечеткой модели управления и при переходах между нечеткими моделями.
Каждая подсистема является многофункциональной компонентой. Последняя версия подсистемы моделирования описана в [41]. Реализация компоненты изменения правила вывода в процессе моделирования ОУ позволит изменять все элементы формальной системы mFS={T,P,A,R,TS} в подсистеме моделирования инструментального средства SETRIAN, поскольку элементы T (термы – лингвистические переменные), P (правила построения правильно построенных формул), A (аксиомы–продукционные правила) изменяются при смене нечетких моделей, TS (триангулярные нормы) изменяются в рамках нечеткой модели управления и при переходах между нечеткими моделями.