Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Гибридные системы, основанные на мягких вычислениях: определение, архитектура, возможности
Аннотация:
Abstract:
| Автор: Ярушкина Н.Г. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15481 |
Версия для печати Выпуск в формате PDF (1.16Мб) |
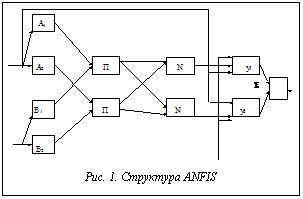
Появление термина мягкие вычисления [1] обычно объясняют тем, что мягкие, или гибридные системы, такие как нечеткие нейронные сети (ННС) с генетической настройкой параметров, демонстрируют взаимное усиление достоинств и погашение недостатков отдельных методов. Очевидно, что представление знаний в нейронных сетях (НС) в виде матриц весов не позволяет строить объяснение проделанного распознавания или прогнозирования, в то время как системы вывода на базе нечетких правил позволяют строить объяснения как обратные протоколы вывода (ответы на вопрос ПОЧЕМУ?). НС обучаются с помощью универсального алгоритма, то есть трудоемкое извлечение знаний заменяется сбором достаточной по объему обучающей выборки. Для нечетких систем вывода построение включает в себя трудоемкие процессы формализации понятий, построения функций принадлежности, формирования правил вывода. ННС же [2,3] обучаются как НС, но строят объяснения как системы нечеткого вывода. Многие интеллектуальные технологии ограничены только анализом ситуации, диагностикой. Интеллектуальные методы, синтезирующие новые изделия, редки. Поэтому специалисты по искусственному интеллекту с надеждой смотрят на методы генетических алгоритмов (ГА) [4,5], решающих задачи структурного синтеза. В гибридных системах ГА способны выполнить настройку функций принадлежности. Функция принадлежности задается параметризованной функцией формы, параметры которой оптимизирует ГА. ГА может оптимизировать и состав больших баз нечетких продукций, и структуру НС, в результате возникают генетические ННС [6]. Для развития большинства прикладных интеллектуальных систем было характерно доминирование символьных методов, так как количественные теории в искусственном интеллекте признавались менее обещающими. В результате для такой насыщенной расчетами области деятельности, как автоматизированное проектирование сложных технических систем, использование интеллектуальных методов дало меньший эффект, чем ожидалось. На наш взгляд, причина состояла в отсутствии среди интеллектуальных методов средств обработки количественных данных. Мягкие вычисления могут составить научную основу для глубинной интеграции интеллектуальных технологий в САПР. Фундаментальная проблема моделирования как восприятия (с помощью НС), так и логического мышления (с помощью логического вывода) в рамках единой модели наталкивается на большое число конкретных технологи- ческих проблем по интеграции моделей и технологий. В настоящей статье рассматривается проблема создания технологичной, то есть воссоздаваемой как программная система гибридной архитектуры, которая позволит получить следующие преимущества: · анализировать состояние объекта в условиях неопределенности с помощью системы нечеткого вывода; · прогнозировать будущие состояния с помощью НС; · проектировать новое структурно-функциональное решение объекта с помощью ГА. Схема интеграции должна решать следующие внутренние задачи системы, основанной на знаниях: - снижать трудоемкость экспликации знаний (формирования функций принадлежности, базы нечетких правил); - придавать нейронным ЭС способность объяснять полученные заключения; - учитывать нечеткость, неточность, неполноту представления знаний и немонотонный характер вывода; - снижать субъективность представленных знаний (функций принадлежности и нечетких правил) с помощью настройки на объективные данные; - оптимизировать базу знаний за счет эволюционного моделирования. Мягкая экспертная система (МЭС) Нечеткие ЭС представляют знания в форме нечетких продукций и совокупности лингвистических переменных. Основу представления лингвистической переменной составляет терм с функцией принадлежности. Способ обработки знаний – это вывод по нечетким продукциям. Мягкой будем называть нечеткую ЭС, которая обладает следующими особенностями. · МЭС для извлечения знаний использует статистические данные, которые интерпретирует как обучающие выборки для ННС. · МЭС представляет знания как совокупность лингвистических переменных (функций принадлежности), нечетких продукций и обученных НС. Редукция множества нечетких продукций выполняется с помощью ГА. · МЭС сочетает шаги вывода по нечетким продукциям с шагами многокритериального выбора решения. Многокритериальный выбор решения является по существу специальным типом продукции [7]. Таким образом, если мягкими называют вычисления, сочетающие теорию нечетких систем, НС, вероятностные рассуждения, ГА и обладающие синергетическим эффектом, то мягкой назовем ЭС, сочетающую перечисленные теории ради того же эффекта взаимного усиления. Архитектура ННС с генетической настройкой Глубинная интеграция нечетких систем и НС, связана с разработкой новой архитектуры элементов НС [8]. Изменение элемента НС для адаптации к нечетким системам может касаться выбора функции активации, реализации операций сложения и умножения, так как в нечеткой логике сложение моделируется любой треугольной конормой (max, a+b-a*b...), а операция умножения – треугольной нормой (min, a*b,...) [9]. Нечеткой обычно называют четкую НС, которая построена на основе многослойной архитектуры с применением "И-", "ИЛИ-нейронов", использующих треугольные нормы. ННС функционирует стандартным образом на основе четких действительных чисел. Нечеткой является только интерпретация результатов. При создании гибридной технологии, кроме объединения систем по данным, можно использовать нейрокомпьютинг для решения частной подзадачи нечетких ЭС, а именно настройки параметров функции принадлежности. Функции принадлежности можно сформировать двумя способами – методом экспертной оценки и на основе статистики. Гибридные технологии предлагают третий способ: в качестве функции принадлежности выбирается параметризованная функция формы (например, гауссова кривая с параметрами b, a), параметры которой настраиваются с помощью НС. Настройка параметров может быть получена в рамках алгоритма обратного распространения ошибки. Таким образом, ННС наряду с классическими нейронами, являющимися пороговыми суммирующими элементами, должна включать в себя «логические» нейроны, моделирующие логические связки. Фундаментальная задача объединения методов перцепции (восприятия) и логического (абстрактного) мышления не могла не отразиться на уровне структуры. В ННС любой из известных архитектур слои нейронов становятся специализированными. Есть слой, выполняющий распознавание, а есть слои, вычисляющие логические формулы и импликации (правила ЕСЛИ… ТО). Причем конкретная схема ННС в отличие от архитектуры зависит от конкретной задачи. На рисунке 1 приведена структура ANFIS (adaptive network based Fuzzy Inference System) адаптивной НС для двух правил: ЕСЛИ x1=A1 И x2=B1 ТО y1=c11*x1 + c12*x2 ЕСЛИ x1=A2 И x2=B2 ТО y2=c21*x1 + c22*x2
y =( w1 * y1 + w2 * y2) / (w1 + w 2). Слои ННС ANFIS выполняют следующие функции. Слой 1 представлен РБФ-нейронами и моделирует функции принадлежности. Слой 2 – это слой И-нейронов, которые моделируют логическую связку И произведением: wi = mAi(x1) * mBi(x2).... Слой 3 вычисляет нормированную силу правила = wi /(w1+w2). Слой 4 формирует значение выходной переменной y(x1,x2) = *yi = * (ci1 * x1 + ci2 * x2). Слой 5 выполняет дефаззификацию: y= *y1 + *y2. Алгоритм обучения предопределяет использование (радиальных базисных функций) РБНФ-элементов. Радиальные постсинаптические элементы вычисляют квадрат расстояния между двумя точками пространства, представляющими вектор весов и входов. Генетической называют нечеткую систему, функции принадлежности и база правил которой спроектированы с помощью ГА. В соответствии с объектами оптимизации выбирают единицу кодирования – хромосому. Для настройки хромосомой выбирают либо одно правило, либо варианты базы правил [6]. В соответствии с кодированием уточняются правила генерации новых хромосом. Функция адаптивности представляет собой механизм нечеткого вывода, который для каждого варианта базы правил строит либо управление для нечеткого контроллера, либо экспертное заключение для диагностической экспертизы. Адаптивный ГА Описанные генетические ННС построены так, что ГА устраняет слабость технологии нечетких систем, связанную с трудоемкостью формирования баз правил. Однако можно рассмотреть и другой гибрид, в котором нечеткая система сыграет роль контроллера ГА, управляя его сходимостью. Применение нечеткого контроллера для управления сходимостью ГА позволило нам сформировать вид ГА, названный адаптивным ГА [10]. Построим ГА с управляемой сходимостью. Основная задача, возникающая на этапе адаптации ГА, состоит в построении механизма смещения процесса поиска в перспективные области значений функции оптимальности. В качестве системы управления эволюцией хромосом в ГА будем использовать нечеткий контроллер типа Мамдани. Предложенную архитектуру гибридной системы приведем на рисунке 2. Структурно-функциональное решение МЭС Инструменты для реализации описанных архитектур должны представлять собой совокупность различных программных продуктов, объединенных логикой работы, то есть основными блоками МЭС должны быть следующие: БД функций принадлежности и БЗ нечетких правил; система нечеткого вывода. классические нейроимитаторы (в том числе многослойные перцептроны, сети Кохонена и др.), работающие в режимах обучения, распознавания, предсказания; ННС различных архитектур; библиотеки разнообразных ГА. Состояние мягких вычислений таково, что исследовательский образец гибридной системы можно сформировать, используя результаты различных международных проектов, доступных в Интернете и предназначенных для исследовательских целей [8]. В частности, в описываемых работах в качестве системы нечеткого вывода использована система FuzzyCLIPS 6.2., классические нейроимитаторы Matlab5.2, библиотеки ГА. Были разработаны средства хранения кортежей с нечеткими атрибутами в среде сервера данных Oracle [11] и ННС. Прикладные интеллектуальные системы Результативность приведенной выше архитектуры проверена в ходе реализации трех следующих проектов: ЭС экономического анализа (ЭА) [12], САПР конструирования технологических стендов контроля изделий [13] и САПР проектирования вычислительных систем [14]. ЭС ЭА предназначена для оценки текущей финансово-хозяйственной ситуации на предприятии на основе данных бухгалтерской отчетности и для выработки рекомендации по формированию стратегии предприятия. ЭС ЭА использует следующие методы мягких вычислений: фаззификацию временных рядов базовых экономических показателей, распознавание тенденций нечетких временных рядов с использованием НС, визуализацию интегрального состояния предприятия, прогнозирование методом нейрокомпьютинга, разработку стратегий на основе нечеткого логического вывода. ННС с генетической редукцией правил позволяют сформулировать систему продукций для анализа тенденций развития предприятия и выработки управленческих рекомендаций на основе обучения.
Применение ГА к оптимизации трафика вычислительной сети (ВС) актуально в связи с широким распространением ВС. К задаче оптимизации топологии ВС адаптирован ГА. Адаптация включает формализацию функции оптимальности за счет моделирования трафика. Для построения функции оптимальности построена модель топологии ВС на основе упрощенных функциональных моделей коммутационного оборудования ВС: концентраторов и коммутаторов. Модель позволяет применить ГА для последующей оптимизации. Исследованы различные виды ГА применительно к задаче оптимизации топологии ВС, в частности, алгоритм «только мутация», эволюционные стратегии, мобильный ГА. Разработана и реализована программная система оптимизации ВС методом ГА. Программа реализована на языке C++ с использованием компилятора и библиотек GNU. Программа может быть откомпилирована под многие операционные системы семейства Unix, кроме того, она тестировалась на платформах FreeBSD, Solaris (Sparс и Intel), IRIX (SGI). Предлагаемая архитектура МЭС продемонстрировала синергетический эффект в ходе разработки и эксплуатации прикладных интеллектуальных систем. Прикладные проекты были успешно реализованы в том числе потому, что ННС заменяют трудоемкое извлечение знаний универсальной процедурой обучения. Список литературы 1. Zadeh L What is soft computing? Soft Computing, 1997, 1, p.1-2 2. Ярушкина Н.Г. Нечеткие нейронные сети. // Новости ИИ, 2001. - № 2-3. 3. Bothe H.-H. Fuzzy Neural Networks. Tutorium, IFSA’97, Prague, 1997. 37 pp. 4. Holland Y. Adaptation in Natural and Artificial Systems. University of Michigan, Press, Ann Arbor,1975. 5. Goldberg D.E. Genetic Algorithms in Search, Optimization and Machine Learning, Adisonwesley Publishing Company, Inc., 1989. 6. Herrera F., Magdalena L. Genetic fuzzy systems Tutorium, IFSA’97, Prague, 1997. 7. Ярушкина Н.Г. Мягкие вычисления в автоматизированном проектировании. // Тр. конф. КИИ’2000. - М.: Физматлит. - 2000. - Т. 2. - С. 479. 8. Fuller R. Hybrid systems. Tutotium. http://www.abo.fi/ ~rfuller/ 9. Schweizer B., Sklar A. Associative functions and abstract semigroups, Publ. Math. Debrecen, 10(1963) 69-81. 10. Наместников А.М. Метод адаптации стандартного генетического алгоритма на основе интеллектуального управления эволюцией. // Сб. тр. междунар. науч.-практ. семинара: Интегрированные модели и мягкие вычисления в искусственном интеллекте. - М.: Наука, Физматлит, 2001. 11. Ярушкина Н.Г., Горбоконенко Е.А. Применение нечеткой СУБД в САПР. // Тр. конгресса: Искусственный интеллект в 21 веке. - М.: Физматлит, 2001. 12. Yarushkina N. Soft Computing and Complex System Analysis // Int. J. General Systems, Vol. 30(1), pp. 71-88. 13. Ярушкина Н.Г. Исследование эффективности генетических алгоритмов для задачи размещения. // Сб. тр. междунар. науч.-практ. семинара: Интегрированные модели и мягкие вычисления в искусственном интеллекте. - М.: Наука, Физматлит, 2001. 14. Ярушкина Н.Г., Пирогов В.В. Автоматизированное проектирование вычислительных сетей методом ГА. // Тр. конгресса: Искусственный интеллект в 21 веке. - М.: Физматлит, 2001. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=687&page=article |
Версия для печати Выпуск в формате PDF (1.16Мб) |
| Статья опубликована в выпуске журнала № 3 за 2002 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формирование программ развития больших систем административно-организационного управления
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Спецификация объектно-ориентированной модели данных с помощью отношений
- Компьютер - хранитель домашнего очага
- Эвристические и точные методы программной конвейеризации циклов
Назад, к списку статей



 Выход ННС формируется по формуле:
Выход ННС формируется по формуле: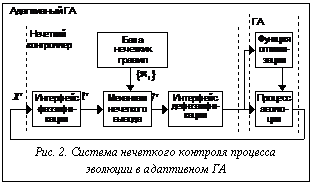 При конструировании стендов изделий конструктором решаются две задачи: выбор корпуса изделия и/или выбор передней панели. Особенностью многих предприятий является наличие в их составе проектного подразделения, которое разрабатывает стенды для испытаний изделия. Можно использовать статистику как обучающую выборку для извлечения правил методом ННС. Для реализации эксперимента по извлечению правил необходимо располагать каким-либо вариантом ННС и обучающей выборкой для ННС, составленной на основании архива проектов. Обучающая выборка должна представлять собой множество строк со сведениями в каждой об одном стенде. Результатом эксперимента является редуцированная ННС, то есть сеть, в которой в результате обучения выжили только существенные правила, а несущественные удалены. Задача размещения элементов стенда в пространстве корпуса решалась в помощью ГА [13].
При конструировании стендов изделий конструктором решаются две задачи: выбор корпуса изделия и/или выбор передней панели. Особенностью многих предприятий является наличие в их составе проектного подразделения, которое разрабатывает стенды для испытаний изделия. Можно использовать статистику как обучающую выборку для извлечения правил методом ННС. Для реализации эксперимента по извлечению правил необходимо располагать каким-либо вариантом ННС и обучающей выборкой для ННС, составленной на основании архива проектов. Обучающая выборка должна представлять собой множество строк со сведениями в каждой об одном стенде. Результатом эксперимента является редуцированная ННС, то есть сеть, в которой в результате обучения выжили только существенные правила, а несущественные удалены. Задача размещения элементов стенда в пространстве корпуса решалась в помощью ГА [13].