Оценка степени изоморфизма на основе нечетких множеств внутренней устойчивости и клик нечетких графов
| Берштейн Л.С. () - , Боженюк А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Одной из важных проблем теории графов является распознавание изоморфизма, или эквивалентности двух графов. Задача состоит в том, чтобы между множествами вершин заданных графов определить существование взаимно однозначного соответствия, сохраняющего отношение смежности вершин [1]. В случае нечетких графов понятие изоморфизма является нечетким. Рассмотрим нечеткие ориентированные графы [2] В работе [3] рассматривалось понятие нечет- кого изоморфизма нечетких графов в виде Нечеткие графы являются обобщением четких графов, которые, в свою очередь, можно рассматривать как квазинечеткие, у которых функции принадлежности принимают два значения – 0 и 1 и, следовательно, значение изоморфизма fÎ{0,1}. Если f=1, то четкие графы изоморфны, если f=0, то нет. Четкие графы характеризуются инвариантами, такими как числа внутренней и внешней устойчивости, хроматическое число и пр. [1]. Если четкие графы изоморфны (f=1), то их инварианты совпадают. Если те или иные инварианты рассматриваемых графов совпадают, то это не значит, что графы изоморфны. В этом смысле совпадение инвариантов является необходимым, но не достаточным условием изоморфизма четких графов. Если инварианты не совпадают, то рассматриваемые графы не являются изоморф- ными. При рассмотрении нечетких графов их инварианты также являются нечеткими величинами. В связи с этим возникает задача оценки влияния нечетких инвариантов на величину возможного изоморфизма f рассматриваемых нечетких графов. В данной работе устанавливается взаимосвязь между степенью изоморфизма и нечеткими множествами внутренней устойчивости и нечеткими множествами клик нечетких графов. Рассмотрим произвольный подграф Определение 1 [4]. Степенью внутренней устойчивости Определение 2 [4]. Подмножество Пусть Определение 3. Множество Свойство 1. Из определения 3 непосредственно вытекает неравенство:
Заметим, что величина Определение 4. Подмножество вершин Определение 5. Подмножество вершин Как и для внутренне устойчивых множеств, рассмотрим семейство всех максимальных нечетких клик Определение 6. Множество Свойство 2. Из определения 6 непосредственно вытекает неравенство:
Величина Построим дополнительный неориентирован- ный нечеткий граф Свойство 3. Семейство максимальных нечетких клик исходного графа Данное свойство непосредственно вытекает из определений максимальной нечеткой клики и максимального нечеткого внутренне устойчивого множества. Из свойства 3 непосредственно вытекает следующее следствие: нечеткое множество клик нечеткого графа Рассмотрим теперь некоторое взаимно однозначное соответствие Свойство 4. Справедливо выражение Доказательство. Перенумеруем вершины множеств X и Y следующим образом: присвоим номера 1,2,…,k вершинам, входящим в подмножества
Рис. 2
Свойство 4 доказано. Свойство 5. Пусть
Доказательство. Если Случай 1. Вершине Случай 2. Вершине Случай 2.1. Справедливо неравенство Случай 2.2. Справедливо неравенство
Рассмотрим вершины
В силу произвольного значения Пусть Свойство 6. Справедливо неравенство Доказательство. Пусть Случай 1.
Рис. 3
Рис. 4
Рис. 5 Случай 2. Случай 2.1. Справедливо неравенство Случай 2.2. Справедливо неравенство
Рассмотрим подмножество вершин Рассмотрев все возможные случаи, мы тем самым доказали свойство 6. Пусть Свойство 7. Справедливо неравенство Данное свойство доказывается аналогично свойству 6. Пример. Рассмотрим пример оценки изоморфизма нечетких графов Нечеткие множества внутренней устойчивости и клик графов
Тогда степень изоморфизма рассматриваемых графов оценится как
Таким образом, степень изоморфизма нечетких графов, приведенных на рисунке 5, не может превышать значения 0,7. Доказанные свойства 6 и 7 позволяют по нечетким множествам внутренней устойчивости и нечетким множествам клик оценивать возможную сте- пень изоморфизма нечетких графов. Необходимо отметить, что оценка степени изоморфизма нечет- ких графов возможна и с помощью других инвари- антов. Список литературы 1. Зыков А.А. Основы теории графов. - М.: Наука. Гл.ред.физ.-мат.лит., 1987. – 384 с. 2. Кофман А. Введение в теорию нечетких множеств. - М.: Радио и связь, 1982. 3. Берштейн Л.С., Карелин В.П., Целых А.Н. Модели и методы принятия решений в интегрированных интеллектуальных системах. - Р-н-Д: Изд-во Ростовского ун-та, 1999. – 278 с. 4. Берштейн Л.С., Боженюк А.В. Определение нечетких внутренне устойчивых, внешне устойчивых множеств и ядер нечетких ориентированных графов //ТиСУ.-1999.-№1. - С.161-165. |
http://swsys.ru/index.php?id=714&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Кросс-система автоматизации разработки программного обеспечения на базе языка высокого уровня Рада
- Система автоматизации процессов рабочего проектирования сложного изделия
- О программной реализации геоинформационных систем
- Реализация теней с помощью библиотеки OpenGL
- Сравнение сложных программных систем по критерию функциональной полноты

 и
и  , где X и Y – множества вершин, а
, где X и Y – множества вершин, а 
 – нечеткие множества ребер с функциями принадлежности соответственно,
– нечеткие множества ребер с функциями принадлежности соответственно,  и
и 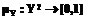 . Пусть число вершин в графах совпадает, то есть
. Пусть число вершин в графах совпадает, то есть  .
. и решалась задача нахождения (или доказательства его отсутствия) такого взаимно однозначного соответствия
и решалась задача нахождения (или доказательства его отсутствия) такого взаимно однозначного соответствия  , при котором величина f достигала некоторого заранее заданного значения
, при котором величина f достигала некоторого заранее заданного значения  . Здесь под
. Здесь под  подразумевается операция минимум, а эквивалентность определяется как
подразумевается операция минимум, а эквивалентность определяется как  , где
, где  – операция нечеткой импликации, в частности, определяемая в логике Лукасевича (a®b=min{1,1–a+b}).
– операция нечеткой импликации, в частности, определяемая в логике Лукасевича (a®b=min{1,1–a+b}).
 нечеткого графа
нечеткого графа  на k вершин (
на k вершин ( ).
). подграфа
подграфа  назовем величину, определяемую как
назовем величину, определяемую как 
 .
. называется максимальным нечетким внутренне устойчивым множеством со степенью внутренней устойчивости
называется максимальным нечетким внутренне устойчивым множеством со степенью внутренней устойчивости  , если справедливо неравенство
, если справедливо неравенство  .
. – семейство максимальных нечетких внутренне устойчивых k вершинных множеств со степенями внутренней устойчивости
– семейство максимальных нечетких внутренне устойчивых k вершинных множеств со степенями внутренней устойчивости  соответственно. Обозначим через
соответственно. Обозначим через  . Если семейство
. Если семейство  , то положим
, то положим  . Величина
. Величина  означает, что в графе
означает, что в графе  существует подграф на k вершин со степенью внутренней устойчивости
существует подграф на k вершин со степенью внутренней устойчивости  .
.
 назовем нечетким множеством внутренней устойчивости нечеткого графа
назовем нечетким множеством внутренней устойчивости нечеткого графа  .
. .
. равна 1, если в графе существует хотя бы одна вершина без петли, а величина
равна 1, если в графе существует хотя бы одна вершина без петли, а величина  равна 0, если в графе существует хотя бы одно ребро со степенью 1.
равна 0, если в графе существует хотя бы одно ребро со степенью 1. назовем нечеткой кликой со степенью
назовем нечеткой кликой со степенью  .
. , если справедливо выражение:
, если справедливо выражение:  , иначе говоря, если любое подмножество
, иначе говоря, если любое подмножество 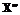 включающее в себя подмножество
включающее в себя подмножество  , является кликой со степенью меньшей величины
, является кликой со степенью меньшей величины  .
. , содержащих ровно k вершин со степенями
, содержащих ровно k вершин со степенями  соответственно. Обозначим через
соответственно. Обозначим через 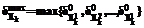 . Если семейство
. Если семейство  . Величина
. Величина  означает, что в графе
означает, что в графе  существует k-вершинный подграф, в котором между любыми двумя вершинами существует ребро со степенью не менее
существует k-вершинный подграф, в котором между любыми двумя вершинами существует ребро со степенью не менее 
 назовем нечетким множеством клик нечеткого графа
назовем нечетким множеством клик нечеткого графа  .
. .
. равна 0, если любой k-вершинный подграф содержит хотя бы одну пару вершин, например
равна 0, если любой k-вершинный подграф содержит хотя бы одну пару вершин, например  , между которыми нет никакого ребра, то есть
, между которыми нет никакого ребра, то есть  .
. , для которого справедливо:
, для которого справедливо: 
 .
. совпадает с семейством максимальных нечетких внутренне устойчивых множеств дополнительного графа
совпадает с семейством максимальных нечетких внутренне устойчивых множеств дополнительного графа 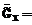
 .
. совпадает с нечетким множеством внутренней устойчивости дополнительного графа
совпадает с нечетким множеством внутренней устойчивости дополнительного графа  .
. между множествами вершин X и Y, в результате которого нечеткие графы
между множествами вершин X и Y, в результате которого нечеткие графы  и
и изоморфны со степенью f. Пусть
изоморфны со степенью f. Пусть  – произвольный нечеткий подграф на k вершин. Обозначим через
– произвольный нечеткий подграф на k вершин. Обозначим через  нечеткий подграф графа
нечеткий подграф графа  , вершины которого
, вершины которого  соответствуют вершинам
соответствуют вершинам  подграфа
подграфа  . Обозначим через fk степень изоморфизма нечетких подграфов
. Обозначим через fk степень изоморфизма нечетких подграфов  и
и  .
. .
. и
и  , а номера k+1,k+2,…,n – оставшимся вершинам из подмножеств
, а номера k+1,k+2,…,n – оставшимся вершинам из подмножеств  и
и  . Тогда степень изоморфизма можно записать в виде:
. Тогда степень изоморфизма можно записать в виде:

 и
и  – степени внутренней устойчивости подграфов
– степени внутренней устойчивости подграфов  и
и  соответственно. Тогда справедливо выражение:
соответственно. Тогда справедливо выражение: (1)
(1)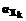 и
и  – степени внутренней устойчивости, тогда в подграфе
– степени внутренней устойчивости, тогда в подграфе  существует пара вершин
существует пара вершин  , для которой справедливо
, для которой справедливо  , а в подграфе
, а в подграфе  существует пара вершин
существует пара вершин  , для которых
, для которых  (рис.1). Рассмотрим два взаимоисключающих случая.
(рис.1). Рассмотрим два взаимоисключающих случая. соответствует вершина
соответствует вершина  , а вершине
, а вершине  соответствует вершина
соответствует вершина  , то есть выполняются равенства
, то есть выполняются равенства  и
и 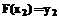 . Тогда величина
. Тогда величина  оценится как
оценится как 
 .
. , а вершине
, а вершине  соответствует вершина
соответствует вершина  , то есть выполняются равенства
, то есть выполняются равенства  и
и  . Причем значения
. Причем значения  и (или)
и (или)  . Тогда справедливо неравенство
. Тогда справедливо неравенство  , откуда следует, что величина
, откуда следует, что величина 
 (рис. 2). Опять рассмотрим два взаимоисключающих случая.
(рис. 2). Опять рассмотрим два взаимоисключающих случая.
 . Тогда величина
. Тогда величина 
 .
. . (2)
. (2) , соответствующие вершинам
, соответствующие вершинам  и
и  ). Справедливо неравенство
). Справедливо неравенство  , откуда следует справедливость условия
, откуда следует справедливость условия . (3)
. (3)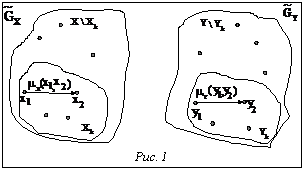 Выполнение неравенства (2) при условии (3) непосредственно влечет за собой справедливость условия
Выполнение неравенства (2) при условии (3) непосредственно влечет за собой справедливость условия  . В этом случае величину
. В этом случае величину 
 свойство 5 доказано.
свойство 5 доказано.
 и
и 
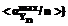 – нечеткие множества внутренней устойчивости нечетких графов
– нечеткие множества внутренней устойчивости нечетких графов  соответственно; f – степень изоморфизма рассматриваемых графов. Тогда справедливо следующее свойство.
соответственно; f – степень изоморфизма рассматриваемых графов. Тогда справедливо следующее свойство. .
. и
и  – некоторые подграфы со степенями внутренней устойчивости соответственно
– некоторые подграфы со степенями внутренней устойчивости соответственно  . Рассмотрим два случая.
. Рассмотрим два случая. , то есть подмножество вершин
, то есть подмножество вершин  соответствует подмножеству вершин
соответствует подмножеству вершин  (рис. 3). Тогда согласно свойствам 2 и 3 можно записать
(рис. 3). Тогда согласно свойствам 2 и 3 можно записать 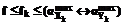 .
.


 (рис. 4). Тогда степень внутренней устойчивости
(рис. 4). Тогда степень внутренней устойчивости  подграфа
подграфа  оценится как
оценится как  . Рассмотрим два подслучая.
. Рассмотрим два подслучая. . Тогда степень изоморфизма оценится как
. Тогда степень изоморфизма оценится как 
 .
. . (4)
. (4) , соответствующее подмножеству вершин
, соответствующее подмножеству вершин  ). Пусть
). Пусть  – степень внутренней устойчивости подмножества
– степень внутренней устойчивости подмножества  . Если выполняется неравенство (4), то обяза- тельно выполнится неравенство
. Если выполняется неравенство (4), то обяза- тельно выполнится неравенство 
 . В этом случае степень изоморфизма оценится как
. В этом случае степень изоморфизма оценится как  .
.
 и
и 
 – не-четкие множества клик нечетких графов
– не-четкие множества клик нечетких графов  и
и  .
. ,
, ,
, ,
, .
.