Генетический алгоритм обучения двухслойного персептрона для задачи классификации образов
| Божич В.И. () - , Кононенко Р.Н. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Генетические алгоритмы являются одним из наиболее мощных средств многопараметрической оптимизации, способных к эффективному поиску глобального оптимума целевой функции (ЦФ). Однако применение стандартного генетического алгоритма к обучению нейронных сетей, в частности персептронов, существенно затрудняется большим количеством обучаемых параметров (весов) нейронной сети и большой степенью их взаимного влияния друг на друга, приводящей к высокой десептивности ландшафта минимизируемой ЦФ – ошибки нейронной сети. В результате обучение посредством генетического алгоритма происходит неудовлетворительно медленно. Одним из возможных способов решения данной проблемы является применение разумной комбинации генетического и градиентного алгоритмов, сочетающей преимущества обоих подходов. Для стандартной сети прямого распространения – персептрона – в роли градиентного алгоритма выступает классический алгоритм обратного распространения ошибки. Персептроны образуют один из наиболее известных классов нейронных сетей прямого распространения. Они используются для решения задач классификации, распознавания образов и нелинейной регрессии [1]. Известно, что двухслойный персептрон при достаточном количестве нейронов в скрытом слое способен произвести произвольное отображение Rn ® Rm. Однако для построения требуемого отображения требуется найти правильные значения весовых коэффициентов нейронов, что представляет собой достаточно сложную задачу. Процесс поиска требуемых значений весов может быть осуществлен на основе различных алгоритмов, называемых алгоритмами обучения персептрона. Известно множество способов обучения персептронов, большинство из которых основаны на алгоритме обратного распространения ошибки [2]. Данный алгоритм представляет собой градиентный спуск в пространстве параметров (весов) нейронной сети, производные по которым определяются процедурой обратного распространения минимизируемой ошибки. Отличительной особенностью данного алгоритма является использование локальной информации при поиске, что с неизбежностью ведет к возможности стагнации алгоритма в локальном минимуме ошибки нейросети и, как следствие, к неудовлетворительным результатам обучения. Существующие модификации обратного распространения, такие как наиболее быстрая модификация Quick Propagation [3] или методы с использованием двух производных, также базируются на локальной информации и не решают проблему локального оптимума, лишь ускоряя градиентный спуск в пространстве параметров. Радикальное решение проблемы локального оптимума может заключаться в применении иных алгоритмов оптимизации, производящих глобальный поиск в пространстве оптимизируемых параметров. В роли алгоритмов этого типа могут быть использованы эволюционные алгоритмы оптимизации, наиболее популярными из которых являются генетические алгоритмы (ГА) [4]. Вопрос применения ГА к обучению нейронных сетей обсуждался в ряде научных статей [5,6], при этом заметно существенное разделение мнений относительно перспективности данного подхода. Несмотря на то что ГА успешно решают задачу обучения нейросети на простых тестовых задачах типа XOR, некоторые известные исследователи [5] сомневаются в возможности масштабирования данного алгоритма при обучении больших нейронных сетей. Одной из основных причин, мешающих эффективному использованию ГА для обучения нейронных сетей, является большое количество параметров оптимизации (даже для сетей среднего размера оно составляет несколько тысяч), а также сильное взаимное влияние весов на ошибку сети, приводящее к десептивности ландшафта ЦФ В работе предпринята попытка адаптации ГА оптимизации к решению задачи обучения двухслойного персептрона в сочетании с классическим алгоритмом обратного распространения ошибки. Целью работы была разработка алгоритма обучения персептрона для задач, в которых обучающая выборка имеет бинарные значения для выходов. Это условие справедливо для случая классификации образов – наиболее частой целевой задачи персептрона. Предлагаемый метод обучения основан на некоторых особенностях работы двухслойного персептрона. Двухслойный персептрон (см. рис.) представляет собой сеть прямого распространения с двумя рабочими слоями (скрытым и выходным). Каждый нейрон выходного слоя связан со всеми нейро- нами предыдущего (скрытого) слоя, первый слой (он же скрытый слой) связан со всеми входами нейро- сети. Работа двухслойного персептрона при бинарных целевых значениях на выходах может быть представлена следующим образом. На входы сети поступает входной вектор из величин xi размерности n. При работе первого слоя сети этот вектор преобразуется в вектор выходных активностей нейронов скрытого слоя Математически персептрон может быть описан следующей системой уравнений:
. . .
. . .
где n – число входов персептрона; m – число выходов персептрона; l – число нейронов в скрытом слое персептрона; xi – значение на i-м входе персептрона; y1... ym – значения на выходах персептрона; Функция активации f (.) Î (0;1) нейрона обычно задается сигмоидой:
Очевидно, что при этом скрытый слой выполняет функцию приведения исходного пространства признаков X к пространству активностей нейронов скрытого слоя Известно, что в задаче классификации однослойным персептроном поверхность ошибки содержит единственный глобальный минимум и, следовательно, обучение однослойного персептрона может быть выполнено с помощью стандартной процедуры градиентного спуска на основе обратного распространения ошибки. Из сказанного можно заключить, что обучение весов 1-го слоя В генотипе особи кодируются только веса скрытого (1-го) слоя 1. При оценке ЦФ особи популяции F внутренний слой сети инициализируется параметрами из хромосомы. 2. Веса wko (k = 1 ,..., l, o = 1,..., m) выходного слоя обучаются классическим алгоритмом обратного распространения ошибки. 3. ЦФ особи вычисляется на основе работы сети после обучения внешнего слоя алгоритмом обратного распространения ошибки. 4. После обучения комбинированным алгоритмом лучшая сеть может быть дообучена на основе обратного распространения ошибки. При таком подходе основное преимущество ГА – способность находить глобальный оптимум – используется только для нахождения значений весов скрытого слоя сети, определяющего внутреннее представление образов. Данная задача имеет множество вариантов решений и локальных экстремумов, отличных по количеству линейно разделимых образов. В решении ГА стремится найти бассейн притяжения глобального минимума ошибки сети. При его нахождении дальнейший спуск к оптимальному значению весов производится градиентным алгоритмом, обучающим выходной слой нейросети. Особенности ГА. В работе применялся стандартный ГА [8]. В качестве оператора селекции использовалась селекция на основе ранжирования [6], что оказалось наиболее эффективным, так как позволяет предотвратить преждевременную сходимость ГА, а также дает возможность сохранить селективную силу на финальных этапах обучения сети, когда все решения имеют примерно одинаковую оценку качества. Оператор кроссовера, взятый из работы [6], оказался более эффективным по сравнению с обычным двухточечным вариантом. Отличительной особенностью его является то, что для каждой пары кодировок соответствующих весов родителей применяется отдельный вариант двухточечного кроссовера. Для групп бит, кодирующих отдельные веса нейросети, данный кроссовер работает как однородный кроссовер (закодированные веса родителей обмениваются между собой с вероятностью 0.5). Последней, и наиболее важной особенностью разработанного ГА является использование целочисленной ЦФ. Данная функция вычисляется как число правильных ответов нейросети, суммированное по всей выборке:
где m – число выходов нейросети; N – число примеров в обучающей выборке; yij – реальное значение на j-м выходе сети для образа i; ytij – требуемое значение на j-м выходе сети для образа i; D=1 при Подобный способ вычисления грубой оценки особей в ГА продиктован следующими соображениями. 1. ГА является средством глобальной оптимизации, позволяющим вести глобальный поиск в пространстве параметров. Вместе с тем локальный поиск с целью уточнения решений предпочтительнее вести алгоритмом, базирующимся на локальной информации, – градиентным методом. С точки зрения оптимизации решение задачи классификации с точностью до некоторого порога является выходом в окрестность глобального минимума ошибки нейросети. После этого обучение производится градиентным алгоритмом. 2. При стандартном значении d=0.5 и достаточном количестве итераций градиентного спуска принятый способ вычисления ЦФ определяет число образов, линейно разделимых в скрытом слое, то есть непосредственно определяет качество работы скрытого слоя. Описание алгоритма обучения. Предлагаемый комбинированный алгоритм обучения двухслойного персептрона имеет следующий вид. 1. Сгенерировать начальную популяцию из N хромосом. 2. Вычислить ЦФ F для особей исходной популяции. 3. Разбить популяцию хромосом на случайные пары. 4. Породить для каждой пары хромосом двух потомков применением оператора кроссовера с вероятностью pc. 5. Применить оператор мутации к каждому из потомков (инверсия бита с вероятностью pm). 6. Вычислить ЦФ F для порожденных потомков. 7. Поместить потомков и родителей в промежуточную популяцию размера 2N. 8. Произвести отбор особей в новую популяцию размера N с помощью оператора селекции на основе ранжирования. 9. ЕСЛИ ЦФ лучшей хромосомы Fmax равна числу обучающих примеров выборки, ТО переход к п.10, ИНАЧЕ переход к п. 3. 10. Инициализировать веса внутреннего слоя персептрона на основе декодирования содержимого лучшей хромосомы. 11. Произвести дообучение сети алгоритмом обратного распространения ошибки. Алгоритм вычисления ЦФ F выглядит следующим образом. 1) Инициализировать веса внутреннего слоя персептрона на основе декодирования содержимого оцениваемой хромосомы. 2) Произвести обучение выходного слоя сети алгоритмом обратного распространения ошибки (t итераций). 3) Подсчитать число правильных ответов сети на основе формулы (3).
Анализ результатов моделирования. В ГА использовалась стандартная бинарная кодировка, каждый вес кодировался 16 битами в интервале [-30;+30]. Размер популяции составлял от 50 до 100 особей в зависимости от решаемой задачи. Количество итераций t обратного распространения в комбинированном алгоритме было принято равным 30 для всех тестовых задач. Скорость обучения при обратном распространении ошибки в комбинированном алгоритме составила 1.0 для задач паритета и XOR и 0.5 для сумматора. Вероятность применения оператора кроссовера была принята равной pc=0.7 для всех случаев. Вероятность мутации бита pc была принята равной 0.001 для задач XOR и паритета и равной 0.005 для задачи сумматора. Параметр ранжирования в операторе селекции был принят равным p=0.99. В таблице приведены результаты работы стандартного (ГА) и предложенного комбинированного (КГА) алгоритмов для решения логических функций XOR, четырехбитового паритета и двухразрядного сумматора. Для каждого случая было проведено 50 испытаний. Формат описания сети в таблице имеет вид: [входы : скрытый слой : выходы]. Как видно из результатов моделирования, предложенный алгоритм существенно превосходит стандартный ГА по скорости сходимости. Для задачи паритета среднее число итераций (поколений ГА) Iсредн, затрачиваемых на обучение, у стандартного ГА превышено почти на порядок по сравнению с предложенным алгоритмом обучения. Для задачи сумматора стандартный ГА не был в состоянии обучить нейросеть за приемлемое время (все запуски были остановлены после достижения максимально установленного числа итераций, равного 5000). Дообучение сети, проводимое после применения КГА, происходит за несколько сотен итераций при конечной квадратичной ошибке, равной 0.001. Это значительно меньше, чем количество итераций, требуемое при обычном обучении персептрона методом обратного распространения ошибки. Данный факт подтверждает предположение о том, что ГА способен обеспечить выход в окрестность глобального минимума ошибки нейросети в пространстве весов. Предложенный алгоритм продемонстрировал существенные преимущества по сравнению с обычным ГА. Это относится как к скорости обучения, так и к проценту успешных обучений нейронной сети. Дальнейшее совершенствование предложенного алгоритма может включать в себя изменение способа кодировки весов нейронов в скрытом слое, а также введение механизмов ранжирования нейронов в скрытом слое с целью решения проблемы симметричных представлений, которая, по мнению ряда исследователей [5,6], может существенно ухудшить качество обучения нейронной сети на основе ГА. Ускорение предложенного алгоритма обучения может быть обеспечено за счет применения неквадратичной ошибки. Предварительные испытания показали, что при ошибке, вычисляемой как гиперболический арктангенс от разности между целевым и реальным откликами сети, скорость обучения КГА увеличивается вдвое для задачи сумматора. Список литературы 1. Ежов А.А. Шумский С.А. Нейрокомпьютинг и его применение в экономике и бизнесе.– М.: МИФИ, 1998. – 224с. 2. Rummelhart D.E., Hinton G.E., Williams R.J. Learning Internal Representations by Error Propagation // Parallel Distributed Processing:Explorations in the Microstructure of Cognition. V.1./ eds.: J.L. McClelland, D.E.Rummelhart. – Cambridge (MA): MIT Press, 1986. – P. 318-362. 3. Falhman S.E. Fast Learning variations on back-propagation: an empirical study. // In Proc. of the 1988 Connectionist Models Summer School. – Morgan Kaufmann, CA, 1998. 4. Goldberg D. E. Genetic Algorithms in Search, Optimization and Machine Learning. –Addison Wesley, 1989. 5. Whitley D. Dominic S., Das R., Genetic Reinforcement Learning with Multilayer Neural Networks/ // Proceedings of the Fourth International Conference on Genetic Algorithms. – Mogran-Kaufmann, 1992. – P. 562 - 569. 6. Korning P.G. Training Neural Networks by Means of Genetic Algorithms Working on Very Long Chromosomes. Technical report. – Aarhus University, Denmark, 1994. 7. Minsky M., Papert S. Perceptrons. – Cambridge (MA): MIT Press, 1969. 8. Whitley D. A Genetic Algorithm Tutorial. – Colorado State University, 1993. |
http://swsys.ru/index.php?id=717&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Компьютерный тренажер для операторов технологических процессов доменного производства
- Подход к выбору оптимального маршрута при перевозке крупногабаритных грузов на основе нейросетевых технологий
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Общедоступные математические САПР для персональных компьютеров класса IBM PC
- Комплекс автоматизированного проектирования геотехнических сооружений "КАППА"

 , k = 1,...,l. Далее выходной слой производит классификацию поданного на входы образа только на основе активностей предыдущего слоя
, k = 1,...,l. Далее выходной слой производит классификацию поданного на входы образа только на основе активностей предыдущего слоя  ,
, , (1)
, (1) ,
, – вес связи от входа i к скрытому нейрону k; wk1...wkm– веса связей от скрытого нейрона k к выходам y1... ym персептрона;
– вес связи от входа i к скрытому нейрону k; wk1...wkm– веса связей от скрытого нейрона k к выходам y1... ym персептрона;  – порог k-го скрытого нейрона; t1...tm – пороги выходных нейронов.
– порог k-го скрытого нейрона; t1...tm – пороги выходных нейронов. , (2)
, (2)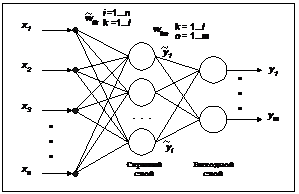 где a – уровень активации нейрона.
где a – уровень активации нейрона. , отображения исходных образов в котором являются уже линейно разделимыми.
, отображения исходных образов в котором являются уже линейно разделимыми. , (3)
, (3) и D=0 в противном случае; dÎ[0;0.5] – величина, определяющая максимально допустимое отклонение реального значения на выходе сети от целевого.
и D=0 в противном случае; dÎ[0;0.5] – величина, определяющая максимально допустимое отклонение реального значения на выходе сети от целевого.![Подпись: Таблица
Результаты моделирования
Тип алго-ритма
Задача
Сеть Размер попу-ляции
Iмин
Iмакс
Iсредн. Неудач-ные
запуски
ГА XOR [2:2:1] 50 1 37 8.64 0
КГА XOR [2:2:1] 50 1 5 1.42 0
ГА паритет [4:4:1] 50 174 4942 1414.33 6
КГА паритет [4:4:1] 50 50 657 155.09 0
ГА сумматор [4:6:3] 100 — — — 50
КГА сумматор [4:6:3] 100 50 111 87.87 0](uploaded/image/2002-1/image935.gif) Еще раз отметим, что при принятом подходе ГА является ответственным за поиск внутреннего представления обучающей выборки в скрытом слое персептрона. Целью ГА является нахождение скрытого представления, отвечающего условию линейной разделимости образов из разных классов. Целью градиентного обучения выходного слоя при оценке ЦФ является определение числа образов, линейно разделимых на скрытом слое персептрона. Когда число разделенных образов равно объему выборки, генетическое обучение прекращается и производится дообучение сети на основе обратного распространения ошибки. В пункте 2 алгоритма вычисления ЦФ и при дообучении сети используется стандартная квадратичная ошибка, позволяющая достичь требуемой точности решения задачи (минимальных величин отклонения реальных выходов сети от требуемых).
Еще раз отметим, что при принятом подходе ГА является ответственным за поиск внутреннего представления обучающей выборки в скрытом слое персептрона. Целью ГА является нахождение скрытого представления, отвечающего условию линейной разделимости образов из разных классов. Целью градиентного обучения выходного слоя при оценке ЦФ является определение числа образов, линейно разделимых на скрытом слое персептрона. Когда число разделенных образов равно объему выборки, генетическое обучение прекращается и производится дообучение сети на основе обратного распространения ошибки. В пункте 2 алгоритма вычисления ЦФ и при дообучении сети используется стандартная квадратичная ошибка, позволяющая достичь требуемой точности решения задачи (минимальных величин отклонения реальных выходов сети от требуемых).