Программная подсистема по исследованию оптимизационных задач на графах
| Курейчик В.В. (vkur@sfedu.ru) - Южный федеральный университет (зав. кафедрой), Таганрог, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Эффективность любого алгоритма может быть доказана в результате теоретического исследования, то есть сравнения оценок временной сложности алгоритма (ВСА) и пространственной сложности алгоритмов (ПСА) и экспериментального исследования, то есть путем проведения тестовых испытаний и сравнения экспериментальных данных использования различных алгоритмов. Объектами исследования являются различные оптимизационные задачи (ОЗ) на графах. Составляются теоретические оценки зависимости быстродействия алгоритма (Y1) и требуемой алгоритмом памяти ОЗУ (Y2) от количества объектов (X1) и количества вершин графа (X2), которым аппроксимируется объект. Параметры Y1 и Y2 не зависят друг от друга. Целью экспериментального исследования являются выявление более точных сведений о зависимостях Y1=F(X1,X2), Y2=F(X1,X2) и проверка теоретических оценок ВСА на практике. Исследование алгоритмов направлено на обеспечение возможности получения ответов на вопросы прикладного характера, например: какое время потребуется для нахождения локального или глобального решения; какие графы алгоритм обрабатывает более эффективно.
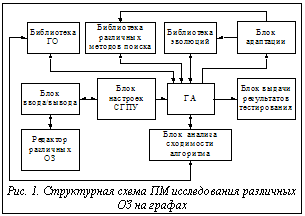
В процессе обработки статистических данных были проведены следующие процедуры: для каждой серии экспериментов определены математические ожидания и законы распределения выходных параметров быстродействия; полученные математические ожидания использованы для проведения регрессионного анализа и построения кривых зависимостей. Для ОЗ на графах общей совокупностью являются всевозможные множества произвольных объектов. Наблюдаемые в последовательности n экспериментов значения образуют частичную совокупность значений случайной величины Y. Степень уверенности, или мера риска (доверительная вероятность) определяется величиной вероятности, с которой делается соответствующее заключение. Допустимая ошибка E при исследованиях устанавливается в зависимости от природы изучаемого явления. В большинстве случаев допустимая ошибка принимается равной 0.05. Для проведения экспериментов выбирался минимально возможный объем выборки, который обеспечил минимальные затраты машинного времени. Программная подсистема по исследованию ОЗ на графах и их процедур выполнена в виде комплекса программных средств, состоящих из различных программных модулей (ПМ). ПМ1 для исследования различных модификаций генетических операторов (оператора рекомбинации, кроссинговера, мутации, инверсии, сегрегации, транслокации, их модификаций и совместного использования). Данный ПМ1 построен на основе простого генетического алгоритма (ПГА) [1-3] и используется для сравнения выходных характеристик одного и того же ПГА для одинаковых графов при использовании различных генетических операторов (ГО). ПМ2 для исследования применяемых в алгоритме эвристических методов поиска, блока итерационного и статистического улучшения. ПМ3 для исследования применяемых в интеллектуальных системах (ИС) моделей эволюций. ПМ4 для исследования применяемых в алгоритме блока адаптации, блока синергетических и гомеостатических принципов управления (СГПУ) [4,5] и предотвращения преждевременной сходимости. При этом выходными параметрами являются: время работы алгоритма, стабильность алгоритма, лучшее решение, достигнутое в процессе работы, оценка алгоритма по сходимости. Общая структурная схема ПМ исследования различных ОЗ на графах приведена на рисунке 1. Программная подсистема реализована на языке Borland C++ под Windows и содержит в себе: панель ввода/вывода, позволяющую загружать/сохранять тестовые примеры (графы с настройками), выводить на печать и т.п; редактор различных ОЗ на графах; панели настроек алгоритма и ввода параметров; панель настроек, позволяющую отключать (или подключать) различные методики улучшения процесса поиска, разнообразные модели эволюций, а также блок адаптации с СГПУ; панель работы алгоритма, позволяющую отображать в процессе работы значение целевой функции (ЦФ), график изменения ЦФ по популяции, абсолютно лучшее значение ЦФ, для оценки выполнения алгоритма. В процессе работы создается файл отчета, содержащий код всех хромосом (решений задачи) всех итераций на текущей генерации, лучшее значение по каждой популяции и результат глобального экстремума. Алгоритм выполнения исследовательского ПМ по тестированию элементов структуры ГА показан на рисунке 2. Выполнение ПМ данной подсистемы начинается с ввода сведений о задачах. Далее выполняется настройка общих и частных параметров алгоритма, к которым относятся: начальное распределение коэффициентов критериев; начальный размер популяции; ограничение на число итераций алгоритма (число шагов); ограничение на число генераций (количество запусков алгоритма); ограничение по значению ЦФ (если не задано – поиск глобального оптимума); вероятности использования ГО. Приведем частные параметры для ПМ (рис. 2): тип операторов кроссинговера (ОК), мутации (ОМ), инверсии (ОИ), сегрегации (ОС), транслокации (ОТ) и функции рекомбинации (ФР) [1-3]. После выполнения всех ГО выполняется проверка ЦФ. При неудовлетворительном значении ЦФ процесс исследования начинается сначала. Частными параметрами для исследования поисковых методов являются использование эвристик на основе статистических методов оптимизации (СМО); градиентных методов (ГМ); методов дихотомии (МД); методов Фибоначчи (МФ); методов золотого сечения (МЗС); фрактальных множеств (ФМ) и др. [5,6]. После выполнения всех известных и разработанных автором поисковых методов выполняется ГА. Если критерий останова достигнут, то выход, если нет, то процесс исследования начинается сначала. Частные параметры для ПМ исследования эволюций с адаптацией на основе СГПУ следующие: использование моделей эволюций Дарвина (ЭД), Ламарка (ЭЛ), Фризе (ЭФ), Поппера (ЭП), блока адаптации (БА), блока анализа и преодоления сходимости и блока СГПУ [5]. После реализации моделей эволюций выполняется ГА. Блоки адаптации и СГПУ отвечают за обратные связи и установление баланса. Далее выполняется непосредственно ГА в соответствии с используемой схемой с установленными ГО, которые влияют в итоге на качественные характеристики поиска. Вычислительная сложность данного алгоритма O(an), где n – число входов. При этом выполняется только генетический поиск.
Сущность данных экспериментов заключается в запуске алгоритмов на одной конкретной задаче с последовательным включением всех разработанных эвристик на одной стандартной задаче и определением значений улучшаемых параметров. Это позволяет оценить эффективность используемых в алгоритме методик оптимизации поиска; или в запуске алгоритмов на некоторых стандартных тестах с последующим сравнением полученных результатов с уже имеющимися для данной задачи (бенчмарками), просчитанными на каком-либо другом алгоритме. Это позволяет оценить практическую эффективность алгоритма и ПМ. Опишем результаты экспериментальных исследований и приведем сравнительные количественные и качественные характеристики для основных ОЗ на графах. Для этого создан комплекс программных средств по анализу разработанных ГА (экспериментального тестирования) и программное обеспечение для решения оптимизационных задач. При построении комплекса программ использовались пакеты Borland C++, Builder, Visual C++. Отладка и тестирование проводились на ЭВМ типа IBM PC c процессором Pentium-III-650, AMD Atlon A(0)-800 с ОЗУ 256 Мб. Для адекватного сравнения использовались стандартные оценки по производительности различных систем (по бенчмаркам), представленных ведущими фирмами мира.
Из приведенных статистических данных следует, что время решения линейно зависит от количества генераций и ВСА с СГПУ лежит между O(anlogn) и O(bn3). Следует заметить, что с увеличением числа итераций в ГА время решения повышается, но это повышение незначительное и компенсируется получением множества локально-оптимальных реше- ний. Для каждого теста условная ЦФ в разрабо- танных автором алгоритмах принимает лучшие значения. Причем эти алгоритмы имеют большее быстродействие, чем метод ветвей и границ, мет- од моделирования отжига и другие аналогичные методы. Количество итераций алгоритмов почти не влияет на качество решения. Зато вероятность применения ГО и их последовательность, порядок реализации ГА с СГПУ являются решающими факторами. Проведены эксперименты для десятков популяций с направленной селекцией, в которых всегда происходил выход из локальных оптимумов. Отметим, что очень важно знать хотя бы вид или поведение критерия оптимальности в зависимости от числа элементов или структуры модели. Кроме использования стандартных операторов, проводились эксперименты с модифицированными ГО. При этом время решения в общем случае возрастало не в линейной, а в квадратичной и кубичной зависимостях. Эксперименты показали, что не всегда увеличение размера популяции улучшает ЦФ. Очевидно, существует какой-то определенный размер популяции, соответствующий оптимальному значению ЦФ, отыскать который чрезвычайно трудно.
Но ПГА и ГА с СГПУ позволяют получать набор локально-оптимальных решений и в частном случае оптимальных решений. Экспериментальные исследования показали, что условная ЦФ для них всегда принимает лучшие значения. Как видно из таблицы, ПГА и ГА с СГПУ по скорости практически совпадают с итерационными, но несколько хуже последовательных. Причем они значительно быстрее, чем методы полного перебора, СМО и их различные модификации. Проведенные серии тестов и экспериментов позволили уточнить теоретические оценки временной сложности алгоритмов оптимизационных задач и их поведение для графов различной структуры. Проведенные комплексные исследования показали улучшение работы предложенных архитектур генетического поиска по сравнению с известными методами. Список литературы 1. Holland John H., Adaptation in Natural and Artificial Systems: An Introductory Analysis with Application to Biology, Control, and Artificial Intelligence. USA: University of Michigan, 1975. 2. Курейчик В.М. Генетические алгоритмы: Монография. - Таганрог: Изд-во ТРТУ, 1998. 3. Goldberg David E. Genetic Algorithms in Search, Optimization and Machine Learning. USA: Addison-Wesley Publishing Company, Inc., 1989. 4. Курейчик В.В. Эволюционные методы решения оптимизационных задач. Монография. Таганрог: Изд-во ТРТУ, 1999. 5. Курейчик В.В. Эволюционные, синергетические и гомеостатические методы принятия решений. Монография. - Таганрог: Изд-во ТРТУ, 2001. 6. Колесников А.А. Основы теории синергетического управления. - М.: Фирма «Испо-Сервис», 2000. |
http://swsys.ru/index.php?id=718&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Эвристические и точные методы программной конвейеризации циклов
- Анализ российского и зарубежного рынков программных продуктов
- Система поддержки принятия решений по планированию профессиональной структуры подготовки специалистов
- Автоматизированная информационная система маркетолога
- Инструментальные и программные средства построения сетевых моделей

 Для проведения объективных тестовых испытаний разработан генератор случайных графов. На вход генератора поступают управляемые параметры X1, X2. Эти параметры принимают дискретные значения. Для формирования достоверных выводов проводится серия опытов-экспериментов. При обработке экспериментальных данных важной задачей является определение (идентификация) закона распределения, к которому можно отнести полученные данные. Если частота наблюдаемых событий близка к величине, предсказываемой теорией, то в дальнейшем можно строить модель исходных или ожидаемых событий на основе теоретического распределения, то есть значительно упрощается проблема дополнительной генерации необходимого количества данных.
Для проведения объективных тестовых испытаний разработан генератор случайных графов. На вход генератора поступают управляемые параметры X1, X2. Эти параметры принимают дискретные значения. Для формирования достоверных выводов проводится серия опытов-экспериментов. При обработке экспериментальных данных важной задачей является определение (идентификация) закона распределения, к которому можно отнести полученные данные. Если частота наблюдаемых событий близка к величине, предсказываемой теорией, то в дальнейшем можно строить модель исходных или ожидаемых событий на основе теоретического распределения, то есть значительно упрощается проблема дополнительной генерации необходимого количества данных.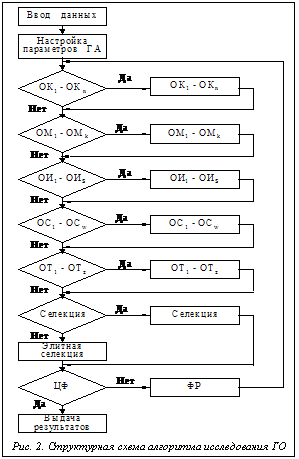 Основная цель эксперимента – подтверждение установленного набора ГО для лучших характеристик по сходимости алгоритма. ВСА в общем случае при всех включенных эвристиках O(an3). Основная цель эксперимента – выявление общего улучшения, вносимого эвристиками в процесс поиска, а также их поведения при различных типах графов. Затем выполняется ГА с неизменным (установленным по результатам проведенного тестирования) набором ГО, с выполнением всех эвристических процедур и моделей эволюций. Основная цель эксперимента – выявление лучших характеристик по времени работы комплекса алгоритмов, а также повышение их стабильности. Для определения показателей улучшения разработанных методик, алгоритмов и ПМ проведен ряд экспериментов, состоящих из трех основных серий – тестирование методик, тестирование ГО и ГА, тестирование моделей эволюций.
Основная цель эксперимента – подтверждение установленного набора ГО для лучших характеристик по сходимости алгоритма. ВСА в общем случае при всех включенных эвристиках O(an3). Основная цель эксперимента – выявление общего улучшения, вносимого эвристиками в процесс поиска, а также их поведения при различных типах графов. Затем выполняется ГА с неизменным (установленным по результатам проведенного тестирования) набором ГО, с выполнением всех эвристических процедур и моделей эволюций. Основная цель эксперимента – выявление лучших характеристик по времени работы комплекса алгоритмов, а также повышение их стабильности. Для определения показателей улучшения разработанных методик, алгоритмов и ПМ проведен ряд экспериментов, состоящих из трех основных серий – тестирование методик, тестирование ГО и ГА, тестирование моделей эволюций. Автор исследовал задачи разбиения графа на части, раскраски графа, размещения вершин графа на плоскости и в линейке, определения пути коммивояжера. Для исследования стандартного графа были реализованы такие классические методы разбиения, как последовательные (КН), итерационные (ПП), поиска в глубину. Отметим, что с попаданием в локальный оптимум увеличение размера популяции, увеличение количества генераций, изменение шкал генетических операторов в большинстве проанализированных примеров не изменяют величины оптимизированной функции. Использование блока СГПУ и комбинированных моделей эволюций, различных типов поиска при незначительном увеличении времени работы алгоритма позволяет решать проблему предварительной сходимости алгоритма и получать оптимальные результаты.
Автор исследовал задачи разбиения графа на части, раскраски графа, размещения вершин графа на плоскости и в линейке, определения пути коммивояжера. Для исследования стандартного графа были реализованы такие классические методы разбиения, как последовательные (КН), итерационные (ПП), поиска в глубину. Отметим, что с попаданием в локальный оптимум увеличение размера популяции, увеличение количества генераций, изменение шкал генетических операторов в большинстве проанализированных примеров не изменяют величины оптимизированной функции. Использование блока СГПУ и комбинированных моделей эволюций, различных типов поиска при незначительном увеличении времени работы алгоритма позволяет решать проблему предварительной сходимости алгоритма и получать оптимальные результаты. Приведем таблицу качественного сравнения различных алгоритмов решения ОЗ на графах. Анализ графика (рис.3) и приведенной таблицы позволяет отметить, что ГА требуют больших затрат времени, чем, например, случайные и последовательные алгоритмы.
Приведем таблицу качественного сравнения различных алгоритмов решения ОЗ на графах. Анализ графика (рис.3) и приведенной таблицы позволяет отметить, что ГА требуют больших затрат времени, чем, например, случайные и последовательные алгоритмы.