Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Общая схема верификации утверждений Р-логики с неизвестными параметрами
Аннотация:
Abstract:
| Автор: Еловков Д.Д. () - | |
| Ключевые слова: утверждение с неизвестными параметрами, программные системы, верификация, хаскел |
|
| Keywords: , , verification, |
|
| Количество просмотров: 14624 |
Версия для печати Выпуск в формате PDF (1.83Мб) |
В последние годы много внимания уделяется методологиям создания качественных программных систем. В этой связи большое количество исследований проводится в области систем типов, верификации, проверки моделей и других механизмов статического анализа программ. Языки программирования сильно различаются по степени надежности и подверженности тем или иным ошибкам. Язык функционального программирования Хаскел [3] считается одним из наиболее надежных языков программирования общего назначения. Чистый функциональный подход обеспечивает полный контроль над побочными эффектами вычислений, исключая большой класс ошибок, присущих стандартным императивным языкам. Развитая система типов позволяет статически гарантировать сложные свойства Хаскел-программ. Одним из исследовательских проектов в области верификации функциональных программ является Programatica. Цель данного проекта – создание средств разработки высоконадежных Хаскел-программ [4]. В рамках проекта были разработаны верификационная логика для Хаскела, P-логика, и автоматический верификатор утверждений P-логики. Средства Programatica позволяют описывать свойства Хаскел-программы, выражая их в виде формул P-логики [1], и в дальнейшем верифицировать их тем или иным способом. Одной из характерных черт инструментов разработки Programatica является то, что свойства можно описывать в любом месте программы, где могут встречаться объявления термов. Это способствует интеграции программирования и верификации в процессе разработки ПО. Для верификации утверждений P-логики с помощью автоматического верификатора Programatica строит логический контекст, в котором следует проверять истинность данного утверждения [2]. Он состоит просто из утверждений эквивалентности, соответствующих определениям выражений, находящихся в области видимости верифицируемого утверждения. Однако для высказывания, определенного внутри функции, в области видимости также будут параметры функции, и корректность высказывания может, конечно же, зависеть от значений этих параметров. Но логический контекст, построенный для такого высказывания, не будет содержать никакой информации о параметрах функции, поскольку их определения недоступны и их значения могут быть любыми, в зависимости от того, как была использована данная функция в том или ином месте программы. Поэтому нельзя верифицировать высказывание P-логики, корректность которого зависит от значений параметров содержащей данное высказывание функции. В настоящей работе предлагается метод верификации таких высказываний. Идея метода состоит в том, чтобы учесть все места в программе, откуда непосредственно или косвенно вызывается функция, содержащая высказывание. Это даст информацию о всех возможных в данной программе значениях параметров нашей функции. И тогда останется лишь проверить, что высказывание истинно при всех этих значениях своих неизвестных параметров. Сначала с функцией, содержащей высказывание, связывается предикат P-логики, которому должны удовлетворять аргументы функции, чтобы высказывание в ней было истинным. Применение функции к аргументам будет считаться корректным только в том случае, если эти аргументы удовлетворяют предикату, связанному с функцией. Этот начальный предикат строится просто связыванием тех переменных в высказывании, которые соответствуют параметрам функции, под знаком предиката. Таким образом, неизвестные параметры высказывания оказываются вынесенными в список параметров предиката. Очевидно, количество и типы параметров предиката будут такими же, как и функции. Далее задача состоит в том, чтобы проверить, что все применения данной функции в программе корректны в описанном смысле. Для этого в каждом терме, определенном через эту функцию, формулируется высказывание, говорящее о том, что аргументы, к которым она применяется, удовлетворяют ее предикату. Но каждое такое высказывание легко может оказаться неверифицируемым стандартными средствами. Для функции g, определенной через нашу исходную функцию f, легко можно получить утверждение, корректность которого зависит от значений параметров функции g. Таким образом произошел переход от одной задачи к некоторому количеству таких же задач для других функций. Выполняя итеративно эту процедуру, построим предикаты для все большего количества функций, которые опосредованно используют исходную функцию. Этот процесс гарантированно завершится на входных точках программы и глобально определенных нефункциональных термах при условии, что рекурсия обрабатывается правильным образом. Действительно, для глобально определенных нефункциональных термов приведенный алгоритм выведет высказывания вместо предикатов, поскольку в области видимости таких термов нет неизвестных параметров. Высказывания, сформулированные в них, верифицируемы стандартными средствами. Что касается входных точек программы, то это либо единственный нефункциональный терм main, либо набор некоторых функций, если программа представляет собой библиотеку или вспомогательный модуль, а не самостоятельную программу. Случай нефункционального терма уже рассмотрен. Для функции же следует принудительно закончить описанную итеративную процедуру, выведя для нее вместо предиката утверждение общезначимости помещенного в нее высказывания, поскольку мы никак не можем контролировать значения параметров функций, которые являются входными точками нашей программы. Поэтому для верифицирования исходного высказывания следует установить его истинность при любых значениях этих по-настоящему неизвестных параметров. Таким образом, получен ряд высказываний, которые можно верифицировать стандартным образом, и истинность которых эквивалентна истинности исходного высказывания в данной программе. Дадим более формальное описание алгоритма. Первым шагом вычислим множество путей в графе вызовов программы, ведущих к функции, содержащей высказывание, Далее алгоритм строит начальный предикат, связанный с исходной функцией путем связывания неизвестных параметров под знаком предиката. После этого для каждого пути итеративно вычисляются предикаты для каждого терма, входящего в данный путь, на основе начального предиката и определений участвующих в пути функций. На фрагменте пути [...hg...] предикат для очередного терма g вычисляется, исходя из предиката, связанного с h, и того, как используется h в определении g. Для этого мы вводим функцию
Таким образом, функция V проходит по пути от исходной функции к функциям, определенным через нее, на каждом шаге связывая с очередной функцией предикат корректности с точки зрения использования ей предыдущей функции в пути. Как уже было сказано, в конце каждого пути получится высказывание вместо предиката. Корректность исходного высказывания будет эквивалентна корректности высказываний, полученных для всех путей. Наиболее существенной частью алгоритма будет функция F, вычисляющая предикат корректности функции на основе ее определения. Для определения F удобно ввести функцию В данном случае получено выражение, представляющее собой применение функции, с которой связан предикат, к некоторым аргументам. Очевидно, утверждением корректности будет удовлетворение аргументов данному предикату. Более интересный пример – условное выражение:
Утверждение корректности в данном случае есть конъюнкция корректности x, и корректности выражений в двух альтернативах, y и z. Причем для альтернатив функция E строит импликации, чтобы утверждения были более слабые и, следовательно, легче верифицируемые. Построение начального предиката будет выполняться исходя из тех же соображений. Например, если исходное высказывание находится внутри одного или нескольких вложенных условных операторов, то оно будет помещено внутрь соответствующих импликаций. Также функция E будет определяться для выражения, где функция, с которой связан предикат, передается другой функции в качестве параметра. Тот факт, что функции в Хаскеле могут передаваться другим функциям и сохраняться в структурах данных, приводит к тому, что любая функция может вызываться в программе не под своим именем. Поэтому какие-то термы, из которых может быть вызвана наша исходная функция, не попадут ни в один из построенных на первом шаге путей. Однако тот терм, где некоторая функция изначально передается другой функции, будет представлен в пути, поскольку в этом терме будет фигурировать ее имя. Определим функцию E для этого случая: Здесь с h связывается предикат, потому что несмотря на то, что она не определена через f, эта функция участвует в вычислении h. Запись Предложенный механизм способствует более тесной интеграции разработки ПО и его верификации, поскольку позволяет описывать верифицируемые инварианты в любых местах программы, даже если эти инварианты формулируются в терминах неизвестных параметров. Без подобного механизма для верификации утверждений с неизвестными параметрами разработчику пришлось бы вручную искать все места в программе, откуда может вызываться функция, содержащая утверждение, и формулировать соответствующе (не всегда тривиальные) утверждения в этих местах. Таким образом, предложенный механизм сокращает время разработки с верификацией, уменьшает вероятность ошибок в спецификации и способствует большей прозрачности программ. Список литературы 1. Kieburtz R. P-logic: property verification for Haskell programs. 2002. (http://citeseer.ist.psu.edu/kieburtz02plogic.html) 2. Kieburtz R. Programmed strategies for program verification. Electronic Notes in Theoretical Computer Science, Volume 174, Issue 10, p. 3-38, 2007. 3. S. Peyton Jones и др. (ред.) Report on the Programming Language Haskell 98, A Non-strict, Purely Functional Language. Technical report, Haskell community. 1999. (http://haskell.org) 4. Команда проекта Programatica. Programatica Tools for Certifiable, Auditable Development of High-assurance Systems in Haskell. 2003. (http://programatica.cs.pdx.edu/P/Programatica Assurance.pdf) |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=752&like=1&page=article |
Версия для печати Выпуск в формате PDF (1.83Мб) |
| Статья опубликована в выпуске журнала № 2 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Синтезирование программ на основе описания графоаналитической модели
- Комплексная верификация результатов прогнозирования характеристик транспортной системы
- Верификация моделей систем на базе эквациональной характеристики формул CTL
- Контроль целостности входных данных при проведении автоматизированного анализа программного обеспечения
- Особенности тестирования наборов данных в операционной системе z/OS
Назад, к списку статей



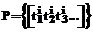 . Путь – это последовательность термов, где первый элемент является термом, определенным через исходную функцию, второй – термом, определенным через первый элемент, и т.д. Нахождение путей – элементарная синтаксическая процедура. Для того чтобы количество и длина путей были конечны, нужно должным образом обрабатывать случай рекурсивного (в том числе и взаимно рекурсивного) определения функций. Рекурсивные определения порождают циклы в графе вызовов. Для каждого цикла оказывается достаточным взять лишь одно повторение соответствующих термов. Например, для функции f, которая в зависимости от какого-либо условия либо вызывает себя рекурсивно, либо возвращает результат с помощью другой функции, получим два пути: [...gf...] и [...gff...]. Первый соответствует вызову g из f, а второй рекурсивному вызову f, и вместе они описывают все возможные варианты путей в месте функции f.
. Путь – это последовательность термов, где первый элемент является термом, определенным через исходную функцию, второй – термом, определенным через первый элемент, и т.д. Нахождение путей – элементарная синтаксическая процедура. Для того чтобы количество и длина путей были конечны, нужно должным образом обрабатывать случай рекурсивного (в том числе и взаимно рекурсивного) определения функций. Рекурсивные определения порождают циклы в графе вызовов. Для каждого цикла оказывается достаточным взять лишь одно повторение соответствующих термов. Например, для функции f, которая в зависимости от какого-либо условия либо вызывает себя рекурсивно, либо возвращает результат с помощью другой функции, получим два пути: [...gf...] и [...gff...]. Первый соответствует вызову g из f, а второй рекурсивному вызову f, и вместе они описывают все возможные варианты путей в месте функции f. , которая строит предикат корректности функции f при условии, что с переменной v в ее определении связан предикат Pv. Введем функцию
, которая строит предикат корректности функции f при условии, что с переменной v в ее определении связан предикат Pv. Введем функцию  , которая для пути, ведущего к функции v, с коей связан предикат Pv, вычисляет предикат (или высказывание) корректности использования функции v по этому пути. Тогда примерное определение V будет следующим:
, которая для пути, ведущего к функции v, с коей связан предикат Pv, вычисляет предикат (или высказывание) корректности использования функции v по этому пути. Тогда примерное определение V будет следующим: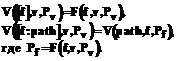
 , которая будет вычислять утверждение корректности выражения. Тогда F будет тривиально определяться через E, просто связывая соответствующие переменные под знаком предиката, получая из высказывания предикат. Функцию E будет удобно определить рекурсивно, отражая рекурсивную структуру Хаскел-выражений. Определение функции E будет заключаться в перечислении возможных видов Хаскел-выражений, которых немного. Например,
, которая будет вычислять утверждение корректности выражения. Тогда F будет тривиально определяться через E, просто связывая соответствующие переменные под знаком предиката, получая из высказывания предикат. Функцию E будет удобно определить рекурсивно, отражая рекурсивную структуру Хаскел-выражений. Определение функции E будет заключаться в перечислении возможных видов Хаскел-выражений, которых немного. Например,  .
.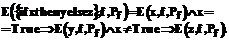
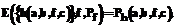 где
где 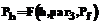 .
. означает предикат корректности h при условии, что на месте ее третьего параметра стоит функция, с которой связан предикат Pf.
означает предикат корректности h при условии, что на месте ее третьего параметра стоит функция, с которой связан предикат Pf.