Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная среда расчетных сеточных моделей для параллельных вычислений
Аннотация:
Abstract:
| Авторы: Копысов С.П. () - , Новиков А.К. () - , Пономарев А.Б. () - , Рычков В.Н. () - , Сагдеева Ю.А. () - | |
| Ключевые слова: расчетные сеточные модели, параллельные решения задач, моделирование |
|
| Keywords: , , modeling |
|
| Количество просмотров: 18242 |
Версия для печати Выпуск в формате PDF (1.83Мб) |
При параллельном решении задач математического моделирования одной из основных проблем является приведение геометрической модели к расчетной. По описанию тела необходимо построить расчетную сетку, затем поставить расчетные условия и разделить сетку для параллельных распределенных вычислений. Все эти этапы требуется выполнять интерактивно и визуализировать результаты. Проблемы параллельных и распределенных вычислений связаны, в частности, с необходимостью подготовки больших объемов начальных данных и обработки массивов полученной информации до и после вычислений на многопроцессорных системах [1-3]. Поэтому актуальным является построение CAE-системы, включающей в себя и специфические функции: подготовку и работу с распределенными данными; функции проверки правильности введенных данных; оптимальную передачу и визуализацию больших объемов данных с возможностью фильтрации ненужной в данный момент информации и др. Структура среды построения расчетных моделей Среда построения расчетных моделей состоит из пяти логических составляющих: геометрия, сетка, расчетная сетка, разделенная сетка и распределенная сетка (строки таблицы). Каждая составляющая содержит компоненты ввода/вывода, объектно-ориентированной модели и визуализации (столбцы таблицы). В таблице перечислены некоторые свойства компонентов, реализованные на соответствующем логическом уровне. Составляющие геометрии и сетки определяют базовый уровень, каждая следующая логическая составляющая зависит от предыдущих уровней. Составляющие допускают наращивание функциональности. Объектно-ориентированная модель разбивается на структуры данных и алгоритмы. Деление на уровни отражает принцип декомпозиции сложных задач на более простые. При построении программной среды стояла задача получить по возможности платформо-независимое программное обеспечение, при этом были использованы следующие технологии: объектно-ориентированное проектирование (UML, Rational Rose), объектно-ориентированное программирование (Visual C++, MFC, CORBA [4]). Структура программной среды FEStudio
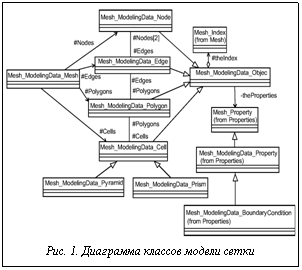
Модель геометрии Создание геометрической модели расчетной области является первым этапом при построении расчетной сетки (первая строка таблицы). Для работы с геометрией на этапе генерации сетки и при выполнении операций над ней (уточнение, огрубление и др.) была использована открытая система геометрического моделирования Open CAS- CADE [5]. Использование классов топологических форм объектов (твердое тело, геометрическая грань, ребро, вершина) позволяет реализовать операции, требующие уточнения сетки по геометрическому описанию области, например, на криволинейных поверхностях. Модель сетки Структура данных для хранения сетки существенно влияет на трудоемкость алгоритмов, а также на скорость реализации сеточной модели. Выбрана структура со связностью объектов вида узлы – ребра – грани – ячейки, содержащая все возможные типы объектов. Объектно-ориентированная модель расчетной сетки. Основу модели сетки (вторая строка таблицы) составляют классы (рис. 1): Object и Mesh. На диаграмме имена классов начинаются с префикса Mesh_ModelingData, который обозначает принадлежность класса логической подсистеме. Класс Object является базовым для всех сеточных объектов. Классы Node, Edge, Polygon, Cell представляют объекты соответствующих размерностей: узел, ребро, грань, ячейка. Между соседними уровнями существует двунаправленная связь: ребро содержит ссылки на образующие его узлы, а узел – на соответствующие ребра. Класс Property присваивает сеточному объекту произвольные свойства, которые хранятся в динамическом списке. В классе Property определены функции сравнения свойств по типу и значению, а также сортировка по типу. На основе данного класса реализуются расчетные данные. Класс Mesh служит контейнером для всех сеточных объектов и свойств, обеспечивает единственность объектов. Новые объекты и свойства создаются вызовом соответствующих функций сетки, которые проверяют наличие такого объекта в списке, если объект уже создан, функция возвращает имеющийся, в другом случае объект вносится в список. Сеточные генераторы. В программной среде реализовано построение неструктурированной 3D-сетки по CAD-геометрии для многосвязных областей, включая параллельное [6]. Перестроение сеток. Реализованы процедуры создания шестигранной сетки из тетраэдальной (делением каждого тетраэдра на 4 гексаэдра), адаптация сетки происходит с учетом CAD-геометрии. Модель разделенной сетки Эффективность параллельного решения задач зависит от качества разделения неструктурированных сеток.
При разделении сетки возникают объекты, принадлежащие двум или более подсеткам. Такие объекты назовем граничными. Процесс разделения сетки содержит следующие шаги. 1. Подготовка объектов. Определяются граничные и внутренние объекты, которые необходимо создать в подсетках, создаются списки объектов, посылаемых в подсетки. 2. Рассылка объектов. Выполняется последовательная рассылка объектов. Последующие процессы выполняются на подсетках параллельно. В подсетках создаются клиенты на граничные объекты. Затем создаются локальные узлы согласно передаваемым координатам, после них – ребра, далее грани и ячейки. Модель распределенной сетки Распределение подсеток и сеточных объектов требует расширения модели разделенной сетки и создания новой подсистемы, описывающей распределенную сетку (пятая строка таблицы), элементы которой находятся в различных адресных пространствах, в том числе, и на различных вычислительных узлах. Распределенная сетка обеспечивает коммуникации между сеткой и подсетками, между подсетками, а также между объектами, находящимися в разных подсетках. В распределенной модели введено понятие остова сетки, который управляет подсетками и организует коммуникации между ними, синхронизирует алгоритмы. Граничные объекты хранятся в остове, а в подсетках создаются заместители, отличающиеся от обычных сеточных объектов только реализацией. Заместители обеспечивают доступ к реальному объекту посредством коммуникаций, реализованных на технологии CORBA [7]. Работа с сеткой, находящейся на удаленном сервере, аналогична работе с обычной сеткой, все преобразования аргументов и вызовы методов выполняют клиент и сервант сетки, связь с удаленным сервером происходит через CORBA (рис. 3). Все преобразования и коммуникации скрыты во внутренней реализации сеточных объектов распределенной модели, что позволяет избежать модификаций используемых алгоритмов. Выделено три стратегии перемещения объектов: 1) перемещение объекта со всеми свойствами (базовая стратегия); 2) перемещение сеточного объекта с созданием некоторых (или всех) его свойств заново (в функции перемещения, у класса, указывается удаление свойства с последующей инициализацией его на другой стороне); 3) удаленный доступ через заместителя объекта без реального перемещения самого объекта. Визуализация На основе модулей Open CASCADE реализовано визуальное приложение расчетных моделей FEStudio [8], содержащее окна отображения геометрии, древовидной структуры документа и окно установки свойств объектов. В библиотеке визуализации сетки реализованы интерфейсы для импорта/экспорта ряда сеточных форматов (GRUMMP, CGNS и др.). Предлагаемая программная среда используется: при создании расчетной сетки и модели; в ходе вычислений при параллельной адаптации сетки к решению и геометрии области; для визуализации полученных сеток и результатов. Применение среды для параллельного построения больших неструктурированных сеток объединило построение и разделение сетки, уменьшая ввод/вывод и расходы на пересылку данных.
1. Tautges T.J. CGM: A Geometry Interface for Mesh Generation, Analysis and Other Applications // Eng. With Computers. – 2001. – V. 17. – P.299-314. 2. Четверушкин Б.Н., Гасилов В.А., Поляков С.В., Якобовский М.В. и др. Пакет прикладных программ GIMM для решения задач гидродинамики на многопроцессорных вычислительных системах // Матем. моделирование. – 2005. – Т. 17. - № 6. – С.58-74. 3. Копысов С.П., Красноперов И.В., Рычков В.Н. Реализация объектно-ориентированной модели метода декомпозиции области на основе параллельных распределенных компонентов CORBA // Выч. методы и программирование. – 2003. – Т.4. – С. 194-206. 4. Цимбал А. Технология CORBA для профессионалов. – СПб: Изд. дом "Питер", 2001. 5. Open CASCADE, simulation integrator: (http://www.opencascade.com) 6. Свидетельство об офиц. рег. в Реестре программ для ЭВМ MultiDomain №2006614109 1.12.2006. 7. Копысов С.П., Пономарев А.Б., Рычков В.Н., Зубцовский С.Н. Расчетные неструктурированные сетки для распределенных вычислений // Сибирская школа-семинар по параллельным вычислениям. - Томск: Изд-во Томского ун-та. – 2005. – С.19-25. 8. Kopyssov S.P., Rychkov V.N., Ponomaryov A.B. The integration of CAD-systems and generators of unstructured 3D mesh // Proceedings of the workshop "Grid generation: theory and applications", June 24-28, 2002, Dorodnicyn Computing Centre RAS, Moscow, Russia. – P. 218-229. | ||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?id=761&like=1&page=article |
Версия для печати Выпуск в формате PDF (1.83Мб) |
| Статья опубликована в выпуске журнала № 2 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Алгоритм и программа расчета напряженно-деформированного состояния песчаных грунтов при циклическом нагружении
- Программа идентификации условий теплообмена для изделий плоской формы
- Разработка и исследование гибридного метода генетического программирования
- Моделирование оптимальных условий биосинтеза
- Моделирование систем массового обслуживания с абсолютным приоритетом
Назад, к списку статей



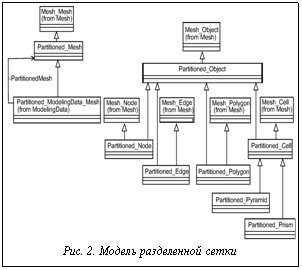
 Данная модель (четвертая строка таблицы) базируется на модели сетки, введенной выше. Классы разделенной модели наследуют соответствующие им классы базовой модели (рис. 2). Особенностью разделенной модели является представление сетки и подсетки одним и тем же классом. Класс Mesh ссылается сам на себя. Таким образом, подсетки могут рассматриваться как самостоятельные сетки, что позволяет применять к подсеткам те же алгоритмы и использовать в тех же расчетах, что и разделенные сетки без изменения программного кода. Примером является алгоритм адаптивного перестроения сетки.
Данная модель (четвертая строка таблицы) базируется на модели сетки, введенной выше. Классы разделенной модели наследуют соответствующие им классы базовой модели (рис. 2). Особенностью разделенной модели является представление сетки и подсетки одним и тем же классом. Класс Mesh ссылается сам на себя. Таким образом, подсетки могут рассматриваться как самостоятельные сетки, что позволяет применять к подсеткам те же алгоритмы и использовать в тех же расчетах, что и разделенные сетки без изменения программного кода. Примером является алгоритм адаптивного перестроения сетки.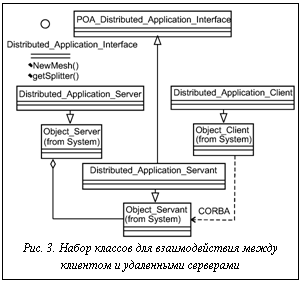 Список литературы
Список литературы