Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм генерации структур управляющего устройства в САПР систем управления
Аннотация:
Abstract:
| Автор: Зотов М.Г. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11063 |
Версия для печати Выпуск в формате PDF (1.22Мб) |
Задача конструирования систем управления из оптимума критерия качества, определяемого многими частными критериями, относится к многокритериальной. Согласно классической схеме ее решения она состоит из нескольких этапов [1-3]: из возможного множества математических моделей изделия отбирается множество допустимых, из него – паретооптимальное, из которого выделяются предпочтительные изделия, для дальнейшего сравнительного анализа по математическим моделям предпочтительных изделий могут быть изготовлены реальные. Очевидно, качество спроектированного с использованием этой схемы изделия, зависит от полноты возможного множества и степени адекватности математических моделей реальным изделиям. Что касается степени адекватности, то, как показывает практика, при проектировании управляющего устройства (УУ) она достаточна, чего не скажешь о полноте возможного множества. В литературе по САПР систем управления [4-7] рассматриваются лишь две структурные схемы УУ, приведенные на рисунке 1а,б. Такая скудость выбора ведет к тому, что спроектированная система управления может быть не лучшей. В связи со сказанным возникают две задачи: 1) показать, что характеристики системы зависят от структуры УУ, 2) разработать алгоритм генерации УУ различной структуры. Первая задача крайне важна. Если характеристики спроектированной системы не зависят от конфигурации структуры УУ, то разработка алгоритма их генерации теряет смысл. Анализ существующих конфигураций структур УУ. На рисунке 1в приведена система управления одномерным объектом с передаточной функцией (ПФ) W0(s). Из этого рисунка видно, что УУ для такого простейшего объекта имеет два входа и один выход. На один из его входов подается задающее воздействие g(t), на другой x(t) – замеряемый выход объекта управления. УУ вырабатывает управляющее воздействие u(t), которое с наложенной на него помехой f(t) подается на вход объекта управления. Таким образом, УУ в системе с одномерным объектом имеет два входа и один выход, то есть является двухканальным. Ввиду того, что рассматриваются линейные системы, сигналы на выходе двух каналов могут объединяться в сигнал управления лишь операцией суммирования или вычитания. Без ограничения общности примем операцию вычитания, ПФ каналов обозначим A1(s) и A2(s). Как было сказано выше, широкое распространение в практике конструирования получили УУ, изображенные на рисунке 1а,б. Из этих схем следуют соотношения:
для схем на рисунках 1а и 1б соответственно. В первом случае
во втором –
К сожалению, дальше использования этих двух вариантов УУ практика проектирования не пошла, что для успешного многокритериального конструирования недопустимо. Конструирование возможного множества УУ. Ранее было установлено, что в системе с одномерным объектом УУ является двухканальным. Введем в рассмотрение динамические звенья с одним входом и одним выходом. Назовем эти звенья корректирующими. Их ПФ обозначим Wi(s) (i=1,2,...). Будем строить УУ на базе этих звеньев. Предположим, что оно построено с использованием одного звена коррекции (ЗК) с ПФ W1(s), тогда A1(s)=F1(W1(s)), A2(s)=F2(W1(s)), A1(s)=F3(A2(s)). (5) Здесь F1 и F2 – функции, раскрывающие характер зависимости A1(s) и A2(s) от W1(s), а F3 – характер зависимости A1(s) от A2(s). Из (5) видно, что ПФ A1(s) и A2(s) функционально связаны, то есть одного ЗК недостаточно для реализации УУ с заранее заданными A1(s) и A2(s). Увеличим число звеньев до двух. В этом случае A1(s)=F1(W1(s),W2(s)), A2(s)=F2(W1(s),W2(s)). (6) Из (6) следует, что в отличие от (5), где ПФ A1(s) жестко связана с A2(s), здесь функции A1(s) и A2(s) развязаны. Действительно, задавая любые, никак не связанные друг с другом значения A1(s) и A2(s), на основе решения системы (6) двух уравнений с двумя неизвестными можно найти соответствующие ПФ ЗК W1(s) и W2(s).
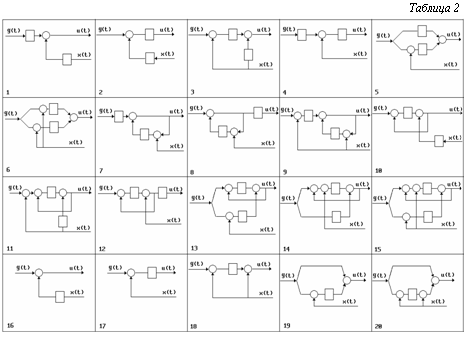
УУ с достаточным числом ЗК. Решение задачи начнем для УУ с двумя ЗК. В УУ с достаточным числом ЗК должно состоять минимум два определяемых ЗК. Дополнительно введем в рассмотрение звено с ПФ, равной единице. Введение такого звена в УУ на его сложности скажется незначительно, но это даст возможность перераспределять внутри него потоки информации. Примем, что ЗК, входящие в УУ, могут быть соединены последовательно и параллельно. При таких предположениях ПФ A1(s) и A2(s) могут иметь с точностью до знака следующий вид: 1, W1(s), W2(s), W1(s)W2(s), W1(s)+W2(s), 1+W1(s), 1+W2(s), 1+W1(s)W2(s), 1+W1(s)+W2(s), W1(s)(1+W2(s)), W2(s)(1+W1(s)), 1+W2(s)(1+W1(s)), 1+W1(s)(1+W2(s)), W1(s)(1+W2(s))+W2(s), 1+W1(s)( 1+W2(s))+W2(s). (7) Функции, входящие в A1(s) и A2(s), взяты только с положительными знаками. Это ни в коей мере не отразится на виде структурной схемы, а повлияет лишь на то, складываются или вычитаются в суммирующем устройстве входные сигналы. Очевидно, что с использованием заданных в (7) соотношений между A1(s) и A2(s) можно построить 15´15 альтернативных конфигураций структур УУ. Отбросим из них те, которые для своей реализации требуют более двух определяемых ЗК. Например, A1(s)=W1(s)W2(s), A2(s)=W1(s)+W2(s), что естественно, так как два корректирующих звена не могут одновременно быть соединенными последовательно и параллельно, для того чтобы это осуществить, необходимо третье корректирующее звено. Из совпадающих (с точностью до индексов) схем оставим только одну. Например, структурные схемы, в которых соблюдаются функциональные соотношения A1(s)=W1(s)W2(s), A2(s)=W1(s)(1+W2(s)), A1(s)= W1(s)W2(s), A2(s)=W2(s)(1+W1(s)), по структуре аналогичны. Аналогичными также являются структуры, в которых A1(a)=W1(s)W2(s), A2(s)= =W1(s)(1+W2(s)); A1(s)=W2(s), A2(s)=W1(s)+W2(s), так как последовательно соединенные звенья с ПФ W1(s) и W2(s) могут быть объединены в одно звено с ПФ W2(s). Структурные схемы, соответствующие случаю, когда A1(s) и A2(s) линейно зависимы, например A1(s)=W1(s)W2(s), A2(s)=1+W1(s)W2(s), отнесем к УУ с недостаточным числом ЗК и рассмотрим их позже. Отброшены альтернативы, где A1(s)=1 либо A2(s)=1. Они также отнесены к классу структур с недостаточным числом ЗК. Анализ показывает, использование приведенных правил отбраковки из 15´15 возможных конфигураций структур оставляет только 56. В таблице 1 приведены номера конфигураций структуры УУ для случаев, когда ПФ A1(s) и A2(s) могут быть вида: W1(s), W2(s), W1(s)W2(s), W1(s)+W2(s). В ней по горизонтали даны значения ПФ A2(s), а по вертикали A1(s). В таблице 2 приведены структуры УУ. Из таблиц 1 и 2 видно, что вторая и третья структурные схемы отличаются от четвертой и пятой только тем, что поменялись местами точки приложения воздействий g(t) и x(t). Если во второй схеме ко входу УУ прикладывалось воздействие g(t), то в четвертой подается x(t). Отметим важную особенность шестой структурной схемы: за счет изменения знака в ней A1(s)¹A2(s). Например, можно принять A1(s)= =W1(s)+W2(s), A2(s)=W1(s)-W2(s). В этом случае конфигурация относится к классу устройств с достаточным числом ЗК.
A1(s)=W1(s)W2(s)/(1+W1(s)), A2(s)=W2(s)/(1+W1(s))+W2(s). Заметим, если решение системы уравнений A1(s)=F1(W1(s),W2(s)), A2(s)=F2(W1(s),W2(s)) приводит к нерациональным ПФ W1(s) и W2(s), то это является признаком того, что такое УУ должно быть отброшено, так как оно не описывается линейными дифференциальными уравнениями. Например, это имеет место для конфигурации, где A1(s)= =W1(s)W2(s), A2(s)=W1(s)+W2(s). Решив эту систему относительно W1(s) и W2(s), получим
ПФ ЗК W1(s) и W2(s) не являются рациональными.
Допустим, что УУ может иметь одну обратную связь. Тогда ПФ A1(s) и A2(s) могут иметь вид: C1(s)/(1+C2(s)). При этом сами C1(s) и C2(s) имеют вид: 1, W1(s), 1+W1(s). При таких предположениях структур с одним ЗК может быть построено 14. Всего же структур с одним и двумя ЗК, построенных по приведенным правилам, 626. В таблице 2 предложены только некоторые из них. Очевидно, что справиться с анализом такого количества альтернатив можно, лишь широко используя вычислительную технику. УУ с дополнительным числом ЗК. Сконструировать множество УУ этого класса можно, используя тот же алгоритм, что был изложен выше для устройств с достаточным и недостаточным числом ЗК. Примем, что УУ состоит из трех ЗК W1(s), W2(s), W3(s), соединенных последовательно и параллельно. Тогда ПФ УУ A1(s) и A2(s) могут быть вида: W1(s), W2(s), W3(s), W1(s)W3(s), W2(s)W3(s), W1(s)W2(s)W3(s), W1(s)+W2(s), W1(s)+W3(s), W2(s)+W3(s), W1(s)(W2(s)+W3(s)), W2(s)(W1(s)+W3(s)), W3(s)(W1(s)+W2(s)), W1(s)(W3(s)+W2(s))+W2(s), W2(s)(W3(s)+W1(s))+W1(s), W3(s)(W1(s)+W2(s))+W2(s), W1(s)(W3(s)+W2(s))+W3(s), W2(s)(W3(s)+W1(s))+W3(s), W3(s)(W1(s)+W2(s))+W1(s). (8) Продемонстрируем построение возможных конфигураций структур УУ на примере, когда ПФ A1(s)=W1(s)(W3(s)+W2(s))+W2(s), а ПФ A2(s) принимает значения из (8). Используя правила отбраковки, аналогичные сформулированным выше, найдем, что из 18 возможных структур УУ останется лишь 7 (рис. 3). На этом же рисунке для третьей конфигурации приведены два возможных варианта схемы с дополнительным ЗК. Дополнительные ЗК выделены индексом «Д». Множество структур с дополнительным чис- лом ЗК может быть существенно расширено за счет введения звеньев с единичной ПФ и обратных связей. Анализ показывает, что при одних и тех же A1(s) и A2(s) характеристики сконструированных систем с УУ различной конфигурации могут существенно отличаться, например, сложностью реализации, чувствительностью ПФ всей системы к изменению ПФ ЗК. Список литературы 1. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. - М.: Наука, 1981. 2. Моисеев Н.Н. Математические задачи системного анализа. - М.: Наука, 1987. 3. Антушев Г.С. Методы параметрического синтеза сложных технических систем. - М.: Наука, 1989. 4. Букатов В.А., Бургонский А.С., Тумаркин В.И., Цейт- лин Я.М. Машинное проектирование систем автоматического управления. - Л.: Судостроение, 1978. 5. Справочник по теории автоматического управления / Под ред. А.А. Красовского - М.: Наука, 1987. 6. Болнокин В.Е., Чинаев П.И. Анализ и синтез систем автоматического управления на ЭВМ. Алгоритмы и программы. - М.: Радио и связь, 1989. 7. Автоматизированное проектирование систем автоматического управления / Под ред. В.В. Солодовникова - М.: Машиностроение, 1990. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=772&page=article |
Версия для печати Выпуск в формате PDF (1.22Мб) |
| Статья опубликована в выпуске журнала № 1 за 2001 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- О моделировании данных
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Гибридная экспертная система проектирования ресурсосберегающих установок первичной нефтепереработки
- Программное обеспечение АРМ медицинского специалиста в области сосудистой патологии
- Подход к выбору оптимального маршрута при перевозке крупногабаритных грузов на основе нейросетевых технологий
Назад, к списку статей



 , (1)
, (1) (2)
(2) , (3)
, (3) . (4)
. (4)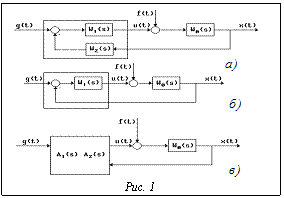 Из соотношений (1-4) следует важное заключение: в первом случае ПФ каналов УУ могут выбираться независимо, во втором они совпадают. Очевидно, схема на рисунке 1а будет обладать лучшими динамическими характеристиками, хотя по сложности УУ она, возможно, и проиграет. Таким образом, ответ о зависимости характеристик системы от конфигурации структуры получен – он положительный.
Из соотношений (1-4) следует важное заключение: в первом случае ПФ каналов УУ могут выбираться независимо, во втором они совпадают. Очевидно, схема на рисунке 1а будет обладать лучшими динамическими характеристиками, хотя по сложности УУ она, возможно, и проиграет. Таким образом, ответ о зависимости характеристик системы от конфигурации структуры получен – он положительный.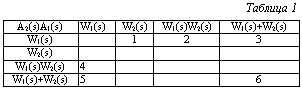 Естественно существование УУ и со звеньями коррекции, ПФ которых определяются из дополнительных условий.
Естественно существование УУ и со звеньями коррекции, ПФ которых определяются из дополнительных условий.
 Обобщая сказанное, констатируем, если в УУ имеются ЗК, определяемые из каких-либо дополнительных условий (например, простоты реализации УУ, уменьшения чувствительности системы к изменению характеристик ее составных частей), то такие устройства объединяются в класс устройств с дополнительным числом ЗК. Подобные ЗК назовем дополнительными. ЗК, ПФ которых вычисляются через ПФ УУ и ПФ дополнительных ЗК, назовем определяемыми. Устройства, где количество определяемых звеньев меньше числа каналов в нем, отнесем к классу устройств с недостаточным числом ЗК; устройства, в которых число каналов совпадает с числом определяемых звеньев, – к классу с достаточным ЗК. Очевидно, что в класс устройств с дополнительным числом ЗК могут входить устройства с достаточным и недостаточным числом ЗК.
Обобщая сказанное, констатируем, если в УУ имеются ЗК, определяемые из каких-либо дополнительных условий (например, простоты реализации УУ, уменьшения чувствительности системы к изменению характеристик ее составных частей), то такие устройства объединяются в класс устройств с дополнительным числом ЗК. Подобные ЗК назовем дополнительными. ЗК, ПФ которых вычисляются через ПФ УУ и ПФ дополнительных ЗК, назовем определяемыми. Устройства, где количество определяемых звеньев меньше числа каналов в нем, отнесем к классу устройств с недостаточным числом ЗК; устройства, в которых число каналов совпадает с числом определяемых звеньев, – к классу с достаточным ЗК. Очевидно, что в класс устройств с дополнительным числом ЗК могут входить устройства с достаточным и недостаточным числом ЗК.
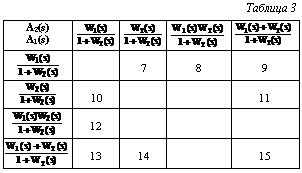 Число систем с двумя ЗК может быть значительно увеличено, если допустить, что УУ может иметь одну обратную связь, тогда ПФ A1(s) и A2(s) могут быть вида C1(s)/(1+C2(s)), в свою очередь C1(s) и C2(s) определяются соотношениями (7). Всего может быть построено 15´15´15 конфигураций структур. Если отбросить совпадающие структуры и структуры, требующие для своей реализации более двух определяемых ЗК, то останется только 199 структур. В таблице 3 приведены номера возможных структурных схем для C1(s) вида: W1(s), W2(s), W1(s)W2(s), W1(s)+W2(s) и C2(s)=W2(s), а в таблице 2 их конфигурации.
Число систем с двумя ЗК может быть значительно увеличено, если допустить, что УУ может иметь одну обратную связь, тогда ПФ A1(s) и A2(s) могут быть вида C1(s)/(1+C2(s)), в свою очередь C1(s) и C2(s) определяются соотношениями (7). Всего может быть построено 15´15´15 конфигураций структур. Если отбросить совпадающие структуры и структуры, требующие для своей реализации более двух определяемых ЗК, то останется только 199 структур. В таблице 3 приведены номера возможных структурных схем для C1(s) вида: W1(s), W2(s), W1(s)W2(s), W1(s)+W2(s) и C2(s)=W2(s), а в таблице 2 их конфигурации.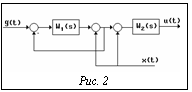 Дополнительное число структур может быть получено, если за основу при построении принять ПФ A1(s) и A2(s), определяемые соотношениями (7), дополнив их ПФ вида C1(s)/(1+C2(s)), где C1(s), C2(s) имеют вид из соотношений (7). Пример такой конфигурации приведен на рисунке 2. ПФ УУ этой конфигурации определяется так:
Дополнительное число структур может быть получено, если за основу при построении принять ПФ A1(s) и A2(s), определяемые соотношениями (7), дополнив их ПФ вида C1(s)/(1+C2(s)), где C1(s), C2(s) имеют вид из соотношений (7). Пример такой конфигурации приведен на рисунке 2. ПФ УУ этой конфигурации определяется так:

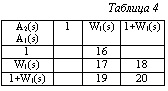 УУ с недостаточным числом ЗК. Обратимся к задаче синтеза структуры УУ с одним определяемым ЗК. Примем, что УУ может содержать не более одного ЗК. При таких ограничениях ПФ A1(s) и A2(s) могут иметь следующий вид: 1, W1(s), 1+W1(s). В таблице 4 с учетом указанных выше правил отбраковки приведены номера всех возможных структурных схем устройства с одним ЗК, а в таблице 2 их конфигурации.
УУ с недостаточным числом ЗК. Обратимся к задаче синтеза структуры УУ с одним определяемым ЗК. Примем, что УУ может содержать не более одного ЗК. При таких ограничениях ПФ A1(s) и A2(s) могут иметь следующий вид: 1, W1(s), 1+W1(s). В таблице 4 с учетом указанных выше правил отбраковки приведены номера всех возможных структурных схем устройства с одним ЗК, а в таблице 2 их конфигурации.