Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Параллельная обработка в алгоритмах визуализации с трассировкой лучей
Аннотация:
Abstract:
| Авторы: Бобков В.А. (bobkov@iacp.dvo.ru) - Институт автоматики и процессов управления ДВО РАН (зав. лабораторией), Владивосток, Россия, доктор технических наук, Роньшин Ю.И. () - , Гуменников В.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15659 |
Версия для печати Выпуск в формате PDF (1.22Мб) |
В работе рассматривается задача балансировки загрузки процессоров при организации параллельных вычислений применительно к алгоритму визуализации пространственных сцен с трассировкой лучей. Исследования проводились на реализованном ранее авторами подобном алгоритме визуализации [1] методом моделирования многопроцессорной обработки на обычной ПЭВМ типа Pentium 2 под ОС Windows. Для моделирования использовались стандартные возможности Windows по имитации многопроцессорности и своя программа для подсчета требуемых временных характеристик. Известно, что эффективность параллельной обработки снижается за счет неравномерности загрузки процессоров, затрат на организацию взаимодействия процессов (процессорное время на выполнение диспетчерских функций и затраты на пересылку данных по каналам связи) и за счет нераспараллеливаемой части работы (подготовка к параллельной обработке и сборка результатов). Для алгоритмов с трассировкой лучей существенно то, что для всех пикселов экрана выполняется алгоритмически одинаковая работа – вычисление точки пересечения с объектом луча, проходящего через пиксел из точки наблюдения. Поэтому разделение работы (загрузки) между процессорами можно осуществлять в пространстве экрана. Всю работу по визуализации сцены можно определить как åqi , где qi – объем работы, связанный с обработкой сцены для i-го луча, проходящего через i-й пиксел. Трудность в равномерном распределении работы состоит в том, что значения qi априори неизвестны и могут существенно различаться между собой. Задача балансировки заключается в поиске такого распределения работы между процессорами, которое бы минимизировало общее время обработки T. Потенциально минимальное время обработки сцены определим как Tmin = Tp / N, где Tp – время обработки сцены одним процессором, а N – количество процессоров. Тогда качество распределения можно оценить параметром e = (T – Tmin) / Tmin, который будет характеризовать отклонение в процентном отношении реального Т от потенциально возможного Tmin. Таким образом, вычисляя e экспериментально или/и теоретически, можно судить о качестве выбранной стратегии распределения. Например, самым простым способом такого разделения может быть разбиение экрана на фрагменты, осуществляемое до начала работы алгоритма визуализации [2,3]. Более эффективной стратегией распределения является метод, основанный на случайной выборке пикселов [4]. Случайная выборка эквивалентна перемешиванию пикселов, что очевидным образом обеспечивает определенную однородность исходного ресурса, предназначенного для разделения. Учитывался еще один фактор, влияющий на конечную эффективность, – использование когерентности в алгоритмах визуализации. Как известно, учет когерентности позволяет уменьшить объем вычислений при последовательной обработке пикселов, связанных геометрическим соседством. Выборка же пикселов экрана в произвольном топологическом порядке будет сводить это преимущество на нет. Поэтому при распараллеливании важно как обеспечение однородности разделяемого ресурса (в данном случае множество пикселов экрана), так и сохранение возможности использования когерентности в алгоритме визуализации. Далее по тексту ту или иную стратегию распараллеливания алгоритма визуализации будем называть методом распараллеливания.
Первый метод статического разделения, традиционный – разбиение экрана на полосы – был реализован для последующего сравнения с ним алгоритмов, предложенных в данной работе. Второй метод основан на механизме случайной выборки, который должен обеспечить высокую степень однородности загрузки. Чтобы сохранить также и преимущества использования когерентности, в качестве минимальной порции работы для «случайного» распределения между процессорами предлагается брать интервал на построчной развертке экрана. В пределах интервала (непрерывной последовательности пикселов) для сокращения объема вычислений алгоритмом визуализации используется когерентность. Сами же интервалы «вырезаются» из траектории развертки случайным образом. При этом достигается компромисс между случайным перемешиванием пикселов и их последовательной обработкой, а размер интервала регулирует соотношение между вкладами «однородности разбиения» и «когерентности» в конечную эффективность алгоритма. В данном алгоритме визуализации когерентность используется на двух этапах его работы – при вычислении параметров луча, проходящего через пиксел экрана, и при работе с октантным деревом в случае изображения параллельной проекции. Динамическое распределение. Рассмотрим типичную схему, когда количество процессов М превышает количество процессоров N и есть диспетчер, запускающий в произвольном порядке ждущие процессы по мере высвобождения физических процессоров. За минимальную единицу работы возьмем строку (столбец) пикселей, подлежащих обработке. Каждому процессу, назначается работа w в несколько строк. Таким образом, w определяет точность балансировки загрузки процессоров. Достаточно очевидно, что в этом случае, с одной стороны, чем меньше w (больше процессов), тем лучше балансировка. Но, с другой стороны, чем больше процессов, тем больше накладные расходы на управление процессами. Существует оптимальное количество процессов, которое определяется параметрами многопроцессорной системы в целом. Во втором методе сделана попытка объединить преимущества случайной выборки и динамической балансировки загрузки. В итоге был реализован гибридный подход, объединяющий в себе как распределение со случайной выборкой и линейной разверткой экрана для начального распределения, так и локальное динамическое перераспределение загрузки. В диспетчерской таблице загрузки процессоров указано, какой объем работы за каждым процессором закреплен и какая часть работы на текущий момент выполнена. Чтобы минимизировать количество операций перераспределения, введены критерии, определяющие, когда и какую часть работы можно забирать у процессора. Соответствующие параметры являются настраиваемыми.
Описание алгоритма визуализации и примеры его работы приведены в [1]. Все вычислительные эксперименты, где N не является параметром, проводились для N = 16. В качестве реального времени работы многопроцессорной системы бралось время работы Т1 “худшего” процессора и время работы диспетчера Т0 (раздача порций работы, балансировка загрузки и сборка результатов). На всех графиках показаны усредненные результаты по нескольким запускам, измеренная экспериментально ошибка находится в пределах 10%. Для первого метода были получены значения T=1.372 и e=0.388. Ниже с этими результатами будет сравниваться эффективность других методов. Заметим, что при e = 0 имеем наилучшее качество, а росту e соответствует его ухудшение. На рисунке 1 представлен график качества распределения (эффективности) для второго метода (количество процессов превышает количество процессоров). График построен для разных задержек tdelay. Задержка имитирует некоторое среднее время взаимодействия рабочего процессора с процессором-диспетчером (для эксплуатируемой МВС-100 скорость передачи 1 Кб по каналам связи с подтверждением запроса соответствует в зависимости от топологии архитектуры диапазону от нескольких мс до 30 мс). График с нулевой задержкой отвечает случаю сверхскоростных каналов связи. Для случаев tdelay=20 мс и tdelay=40 мс имеют место оптимумы. Для первого – при числе процессов М=80 время выполнения Т=1.118, для второго – при М=48 время Т=1.202.
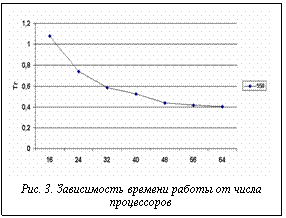
На рисунке 3 показана зависимость времени выполнения (для оптимальной длины интервала 400) от числа процессоров. На графике видно, что, начиная с некоторого числа процессоров, прогресс в быстродействии системы падает. На рисунке 4 показана эффективность e в четвертом методе для разных задержек. Здесь мы видим, что, благодаря динамической балансировке, эффективность с ростом размера интервала уже так не ухудшается, как в методе 3. В то же время имеется оптимум в районе 650 пикселов для tdelay = 20 и 1500 пикселов для tdelay = 40 мс. На рисунке 5 а,б показаны зависимости времени работы алгоритма визуализации от задержки для двух сцен, различающихся по трудоемкости обработки. Для построения графиков брались лучшие времена для каждой задержки. Горизонтальной прямой показан лучший результат для метода 3. Точка пересечения показывает задержку (скорость канала), при которой эффективность методов 3 и 4 выравнивается. Из сравнения результатов видно, что для более трудоемкой сцены преимущество метода 4 перед методом 3 наступает уже при меньших значениях скорости канала связи. Сравнительные результаты представлены на диаграммах рисунка 6 а,б (лучшее время выполнения и лучшее качество распределения для всех рассмотренных методов). Из первой диаграммы видно, что лучшее время дает 3-й метод – статический вероятностный, за исключением случая, когда время задержки близко к нулю (высокая скорость передачи данных между процессорами). Для этого случая эффективность выше у динамических методов. Этот результат ожидаем, поскольку динамическая балансировка требует затрат, которые при статическом распределении отсутствуют. Из анализа приведенных результатов можно сделать следующие выводы. · Для систем с низкоскоростными каналами · С ростом сложности сцены преимущество метода 4 перед методами 3 и 2 начинает проявляться уже на менее скоростных каналах связи. · Используя полученные зависимости, можно указать оптимальное (с точки зрения прироста эффективности) число процессоров. Исследования проводились при финансовой поддержке РФФИ (проект № 99-07-90473). Список литературы 1. Бобков В.А., Роньшин Ю.И. Алгоритм визуализации с трассировкой лучей в октантных деревьях. // Информационные технологии. - 2001- №1. 2. Ван Рем Ф., Ламотэ В., Флеракерс Э. Методы ускорения трассировки лучей с использованием MIMD-архитектуры // Программирование. - 1992. -№4. - с.50-61. 3. Белов С.Б., Бобков В.А., Май В.П., Роньшин Ю.И. Параллельные вычисления в алгоритме визуализации пространственных объектов, построенных методом конструктивной геометрии // Программирование. - 1994. - №2. - С. 16-26. 4. Salmon J. A Mathematical analysis of the scattered decomposition. Proceedings of the Third Caltech Conference and Applications (Pasadena, January), ACM Press, 1988, pp. 239-240. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=773&page=article |
Версия для печати Выпуск в формате PDF (1.22Мб) |
| Статья опубликована в выпуске журнала № 1 за 2001 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Эвристические и точные методы программной конвейеризации циклов
- Эволюционная модель формирования структур виртуальных предприятий
- Комплекс автоматизированного проектирования геотехнических сооружений "КАППА"
- Компьютерные технологии сегодня: тенденции и прогнозы
- Спецификация объектно-ориентированной модели данных с помощью отношений
Назад, к списку статей



 Методы распараллеливания. Сравнительный анализ был проведен на результатах вычислительных экспериментов с четырьмя методами – стратегиями распараллеливания. Два из них выполняют статическое распределение (до начала работы) и два – динамическое (в процессе работы) перераспределение загрузки. Предполагалось, что весь объем данных по сцене для рассматриваемого алгоритма визуализации может быть загружен на каждый процессор (для используемой МВС-100 это так). Для варьирования затрат времени на передачу данных в модель введен параметр tdelay, который был реализован программной задержкой. Зная характеристики для конкретной многопроцессорной системы, можно настраивать параметр tdelay. Во всех рассмотренных ниже методах функции диспетчера (первоначальное распределение и перераспределение работы, сборка результатов) выполняет один из процессоров.
Методы распараллеливания. Сравнительный анализ был проведен на результатах вычислительных экспериментов с четырьмя методами – стратегиями распараллеливания. Два из них выполняют статическое распределение (до начала работы) и два – динамическое (в процессе работы) перераспределение загрузки. Предполагалось, что весь объем данных по сцене для рассматриваемого алгоритма визуализации может быть загружен на каждый процессор (для используемой МВС-100 это так). Для варьирования затрат времени на передачу данных в модель введен параметр tdelay, который был реализован программной задержкой. Зная характеристики для конкретной многопроцессорной системы, можно настраивать параметр tdelay. Во всех рассмотренных ниже методах функции диспетчера (первоначальное распределение и перераспределение работы, сборка результатов) выполняет один из процессоров.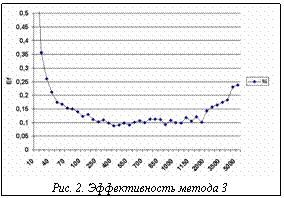 Статическое распределение. При статическом распределении количество процессов равняется количеству процессоров и загрузка в процессе работы не корректируется.
Статическое распределение. При статическом распределении количество процессов равняется количеству процессоров и загрузка в процессе работы не корректируется.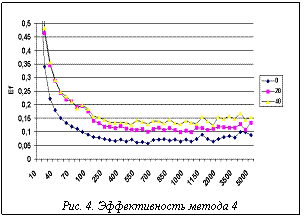 Обсуждение результатов
Обсуждение результатов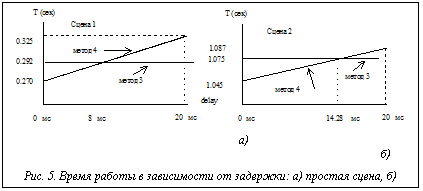 На рисунке 2 показана зависимость качества распределения от длины интервала развертки в методе 3. Наилучшее качество получилось для длины интервала около 400 пикселов. Вместе с тем имеется достаточно хорошо выраженный диапазон (размер интервала примерно 200 – 2000 пикселов), где качество распределения сравнительно хорошее.
На рисунке 2 показана зависимость качества распределения от длины интервала развертки в методе 3. Наилучшее качество получилось для длины интервала около 400 пикселов. Вместе с тем имеется достаточно хорошо выраженный диапазон (размер интервала примерно 200 – 2000 пикселов), где качество распределения сравнительно хорошее.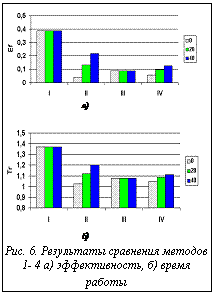 связи из рассмотренных методов оказался эффективнее метод 3 – статический, со случайной выборкой. Для многопроцессорных систем с высокоскоростными каналами лучший результат дают методы с динамической балансировкой загрузки процессоров – методы 2 и 4. Для каждого метода можно выбрать параметр l (длина интервала развертки), обеспечивающий наибольшую эффективность.
связи из рассмотренных методов оказался эффективнее метод 3 – статический, со случайной выборкой. Для многопроцессорных систем с высокоскоростными каналами лучший результат дают методы с динамической балансировкой загрузки процессоров – методы 2 и 4. Для каждого метода можно выбрать параметр l (длина интервала развертки), обеспечивающий наибольшую эффективность.