Система поддержки принятия решений на базе моделей и методов возможностной оптимизации
| Язенин А.В. () - , Сорокин С.В. (sergey@tversu.ru) - Тверской государственный университет, Тверь, Россия | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Возросшая сложность задач принятия решений в управлении производством, финансами и в других отраслях человеческой деятельности, с одной стороны, и развитие вычислительной техники и математического аппарата теории принятия решений, с другой стороны, привели к возникновению и развитию программных систем поддержки принятия решений (СППР). Такие системы обеспечивают поддержку лицу, принимающему решения (ЛПР), на этапах сбора и хранения больших объемов информации, обработки полученной информации с использованием различных методов принятия решений в зависимости от класса поставленной задачи; выбора оптимальной альтернативы и выдачи рекомендаций по реализации полученного решения. В последнее время выработались критерии, которым должны удовлетворять интеллектуальные СППР. Приведем основные из них [1]: · интеллектуальные системы должны быть системами, основанными на знаниях; · интеллектуальные системы должны быть модельно-ориентированными, то есть они должны обеспечивать инструментарий для создания модели принятия решения; · интеллектуальные системы поддержки принятия решений должны обеспечивать возможность работы с различными видами неопределенности, использование и манипулирование нечеткими целями-ограничениями. Многие практические задачи могут быть представлены моделями линейного программирования. В настоящее время теория классического линейного программирования хорошо разработана и реализована в различных программных системах. Однако в связи с недостатком информации или самой сутью проблемы может оказаться невозможным точное определение значения параметров задачи и применение аппарата линейного программирования. Часто диапазоны изменения параметров модели строятся по экспертным оценкам. Адекватным средством моделирования такой информации является современная теория возможностей. Ввиду этого многие практические задачи могут быть представлены моделями возможностного программирования. Практическое применение моделей возможностного программирования делает актуальной разработку соответствующих СППР. Представленная в этой статье СППР FIESTA (Fuzzy Intelligent System) является интеллектуальной в условиях нечетких данных. Система FIESTA обеспечивает: · выбор модели принятия решений; · настройку системы принятия решений в соответствии с выбранной моделью принятия решений; · управление базой данных моделей возможностного программирования; · представление и обработку нечетких данных; · решение задачи по выбранной модели. Система FIESTA может быть использована для поддержки процесса принятия решений при решении задач производственного планирования, в качестве интеллектуального компонента САПР при выборе параметров проектируемых изделий, в гибких производственных системах, при решении задач оперативного управления. Методы решения задач возможностного программирования Для решения задач возможностного программирования в СППР FIESTA применяются непрямые методы возможностного программирования, суть которых состоит в сведении задачи возможностной оптимизации к детерминированной эквивалентной задаче. Задачи возможностного программирования в СППР FIESTA сводятся в ряде случаев к задачам линейного программирования специальной структуры. Их решение базируется на методах линейного программирования. Для решения детерминированных эквивалентов некоторых моделей возможностной оптимизации разработаны оригинальные методы [2]. Введем некоторые базовые понятия теории возможностей, которые потребуются для описания моделей, поддерживаемых СППР FIESTA. Пусть G – множество с элементами g. P(G) – мощность-множество G. Определение 1. Мера возможности P есть функция множеств P: P(G)®[0,1] обладающая свойствами: 1. P(Æ)=0, P(G)=1, 2. П Двойственное понятие для меры возможности вводится посредством меры необходимости n: P(G)®[0,1] : n(A)=1-P(Ac). Тройку (G,P(G),P) называют возможностным пространством. Определение 2. Отображение X: G®E1, возможные значения которого ограничены распределением возможностей X(x)=P{gÎG: X(g)=x} "xÎE1, называют возможностной переменной. Функция возможностей для совокупности возможностных переменных X1,…,Xn определяется следующим образом: mx1,…,xn(x1,…,xn)=P{gÎG: X1(g)=x1,…,Xn(g)=xn} = P{X1-1(x1)I…IXn-1(xn)}. Определение 3. Пусть X1,…,Xn – совокупность возможностных переменных. Будем называть эту совокупность несвязанной, если "{i1,…,ik} mxi1,…,xik(xi1,…,xik)=min {mxi1 (xi1),…, mxik(xik)}. В приводимых далее моделях возможностной оптимизации нечеткие параметры моделируются возможностными переменными. При реализации этих моделей первоочередной является задача определения (построения) функций распределения возможных значений нечетких параметров. Ниже приведены поддерживаемые системой модели критериев и ограничений задач возможностного программирования. Проблема модальной оптимизации состоит в максимизации модального значения функции f0, вида f0(x,g)=SjÎ1:n a0j(g)xj, где a0j являются несвязанными возможностными переменными с унимодальными распределениями возможностей и имеют модальные значения m0j. Максимаксная модель. Максимаксная модель критерия задачи возможного программирования: k®max, П{ SjÎ1:l a0j (g) xj =k} ³ a, aÎ(0,1], где a0j(g) являются несвязанными возможностными переменными. Задача максимизации возможности достижения нечеткой цели представляется моделью: P{a0j(g)xj=b(g)}®max. Максимизация возможности достижения целей-ограничений представляется моделью: P{SjÎ1:l aij xj =bi (g), i=1,…,m}®max. Модальные ограничения имеют вид M{fi(x,g)} £, =, ³ 0. Пусть fi(x,g)=SjÎ1:n aij (g) xj – bi(g) и aij, bi являются несвязанными возможностными переменными с модальными значениями maij, mbi соответственно. В этом случае эквивалентное ограничение имеет вид SjÎ1:nmaij xj-mbi £, =, ³ 0. Ограничения по возможности и необходимости. СППР Fiesta работает с ограничениями на меру возможности вида P{SjÎ1:n aij(g)xj = bi(g)} ³ a и P{SjÎ1:n aij(g)xj £ bi(g)}³a, а также с ограничениями по мере необходимости вида n{SjÎ1:n aij(g)xj £ bi(g)}³a. Работа с нечеткой информацией В ходе разработки СППР FIESTA большое внимание было уделено разработке методов работы с нечеткой информацией. Пользователю предоставляется возможность настроить интерфейс системы в зависимости от его познаний в теории возможностей. При работе со специалистами, знакомыми с понятиями теории возможностей, система позволяет оперировать нечеткими данными на параметрическом уровне. Пользователь может выбрать один из типов распределения возможностей (детерминированное число, триангулярное, трапециевидное, нормальное, возрастающее и убывающее) и задать соответствующие параметры распределения (границы интервала толерантности или модальное значение и коэффициенты нечеткости). Выбор пользователя поддерживается графиком функции распределения текущей нечеткой величины. Во многих случаях с практическими СППР работают лица, не являющиеся специалистами в области нечеткого программирования и теории принятия решений. Для работы с этой категорией пользователей в СППР FIESTA предусмотрен режим "помощник". Этот режим реализован в виде меню-системы, позволяющей на семантическом уровне извлечь из пользователя информацию, необходимую для восстановления возможностного распределения. Меню содержит следующие альтернативы-шаблоны. · Коэффициент мал, он меньше ___, но с наибольшей возможностью он меньше ___. · Коэффициент может меняться в диапазоне от ___ до ___, но наиболее возможное значение равно ___. · Коэффициент может меняться в диапазоне от ___ до ___, но наиболее возможное значение меняется от ___ до ___. · Коэффициент большой, он больше ___, но с наибольшей возможностью он больше ___. · Коэффициент может принимать любое значение, но с наибольшей возможностью он принимает значения около ___. · Коэффициент имеет значение ___. Выбрав одну из альтернатив и проведя ее спецификацию, пользователь предоставляет системе необходимую информацию для восстановления возможностного распределения. Кроме этих двух вариантов работы с известными распределениями возможностей, предусмотрен режим восстановления распределения по предъявляемым значениям. Для восстановления распределений используется метод оценки максимума m/E, описанный в [3]. Этот метод позволяет восстановить унимодальное распределение известного типа по выборке.
Архитектура системы FIESTA При разработке СППР FIESTA была выбрана объектно-ориентированная концепция построения системы. Применение принципов объектно-ориентированного программирования позволило разработать гибкую архитектуру программного обеспечения, позволяющую с минимальными затратами на программирование расширять возможности системы. FIESTA реализована на языке C++ с применением библиотеки классов Microsoft Foundation Classes (MFC). Использование библиотеки MFC позволило сократить временные затраты на разработку интерфейса пользователя без ущерба для конечного результата и тем самым уделить больше времени разработке систем работы с нечеткими данными. Иерархия классов СППР FIESTA включает около 40 классов, образующих подсистемы: · хранения, визуализации и обработки нечетких данных; · генерации задач возможностной оптимизации; · работы с распределениями возможностей. Подсистема хранения, обработки и визуализации нечетких данных В СППР FIESTA имеется ряд классов, представляющих понятия и сущности теории возможностей. Это прежде всего класс CFVariable, представляющий возможностную переменную, и классы, представляющие модели критериев и ограничений. Класс CFVariable инкапсулирует информацию, необходимую для описания возможностной переменной, и содержит методы, обеспечивающие чтение и запись этой информации в файл, а также доступ к параметрам распределений и границам a-уровней распределения. Классы, соответствующие моделям критериев задач возможностного программирования, наследованы от класса CFModel. Базовым классом для классов, реализующих модели ограничений, является класс CConsModel. Основная функция этих классов – построение детерминированных аналогов соответствующих критериев и ограничений задач возможностной оптимизации. В данный момент в системе реализованы классы, соответствующие четырем моделям критериев, и трем моделям ограничений, описанным ранее. Алгоритмы построения детерминированных аналогов, использованные в этих классах, базируются на работах А.В. Язенина [2,4]. Новые модели могут быть легко добавлены в систему путем порождения новых классов от соответствующего базового класса. Хранение задачи возможностного программирования и управление процессами изменения и обработки данных осуществляется объектом CfuzzyDoc. Этот объект отвечает за сохранение и загрузку задач, обеспечивает интерфейс доступа к данным задачи для других подсистем и объектов, управляет процессом создания детерминированных аналогов и решения задач. Объект CFuzzyDoc взаимодействует с объектом CFuzzyView, обеспечивающим отображение задачи в окнах приложения и обрабатывающим команды пользователя. Базовым классом для классов, обеспечивающих построение детерминированных аналогов и решения задач возможностного программирования, является класс CLPExport. Этот класс предоставляет базовый интерфейс для создания и хранения детерминированных задач линейного программирования. Экспорт детерминированных аналогов обеспечивается классом CMPSExport, который является потомком класса CLPExport и дополняет его интерфейс функцией записи сгенерированной детерминированной задачи в файл формата MPS. Другим потомком класса CLPExport является класс CsimplexSolver, реализующий симплекс-метод решения задач линейного программирования и сохраняющий полученный результат. Решение задач сепарабельного программирования обеспечивается классом CAdvSolver, являющимся потомком класса CSimplexSolver. Этот класс обеспечивает построение аппроксимирующей задачи в l-форме и решение полученной задачи модифицированным симплекс-методом [5]. Подсистема генерации задач возможностной оптимизации Данная подсистема обеспечивает построение модели возможностной оптимизации в диалоге с пользователем. Система состоит из классов CnewDocWizard, CWizNewStep1, CWizNewStep2, CwizNewStep3 и CWizNewStep4. Класс CNewDocWizard позволяет хранить полученную от пользователя на разных этапах информацию и передавать ее классу CDocument для создания новой задачи. Этот класс хранит: информацию о размерности задачи; моделях критерия и ограничений; имена переменных, ограничений и целевых функций. Классы CNewStep1,…,CNewStep4 обеспечивают извлечение информации из пользователя на разных этапах диалога. На первом этапе вводится имя генерируемой задачи и выбирается модель критерия. Затем определяется размерность задачи. На третьем этапе определяются названия и модели ограничений задачи. После сбора всей информации на четвертом этапе пользователю предъявляется описание генерируемой задачи. Если пользователь удовлетворен этим описанием, то диалог завершается, в противном случае пользователь может вернуться к предыдущим шагам и внести необходимые изменения. Подсистема работы с распределениями возможностей Подсистема состоит из классов CFParamDlg, CFDisplay, CFuzzyWizDlg, CEstimateDlg. Классы CFParamDlg и CFDisplay обеспечивают редактирование распределений возможности в режиме задания параметров распределения. Этот режим ориентирован на пользователей, владеющих понятиями теории возможностей. Класс CFParamDlg обеспечивает функционирование диалогового окна, в котором пользователь выбирает тип распределения и вводит необходимые параметры. Класс CFDisplay реализует окно отображения получаемой функции распределения возможностей. Класс CFuzzyWizDlg обеспечивает работу с распределениями возможностей в режиме "помощник", ориентированном на неподготовленных пользователей. Класс CEstimateDlg обеспечивает восстановление распределения возможностей по представленной выборке экспертных значений. Пример решения задачи с использованием системы FIESTA Рассмотрим задачу максимизации возможности выполнения нечеткой цели: P{a01x1+a02x2+a03x3=b0}®max с тремя ограничениями: x1+x2+x3³5.6, P{a21x1+a22x2=b2}³0.5, P{2x1-x2+3x3=b3}³0.5,
где a01, a02, a03 – триангулярные нечеткие переменные с параметрами (2;1;1), (1;1;0.5) и (15.24;1;1) соответственно; a21, a22, b2 – нормальные нечеткие переменные с параметрами (1;2), (1;2), (2;2) соответственно; b3 – трапециевидная нечеткая переменная с параметрами (10;13;1;1). Все нечеткие переменные являются мини-связанными.
После получения ответа на все вопросы система создает модель задачи с нулевыми коэффициентами и отображает окно, содержащее эту задачу. Теперь пользователь должен задать значения всех параметров задачи. На рисунке 2 показан процесс задания коэффициента b3 нашей задачи. Вид окна задачи после задания всех параметров показан на рисунке 3. После того как все параметры заданы, пользователь активизирует пункт “Решить” меню “Решение” и получает решение задачи (рис. 4).
Дальнейшее развитие СППР FIESTA будет связано с разработкой и реализацией методов коррекции задач возможностного программирования, позволяющих корректировать и решать задачи, которые в своей исходной постановке являются противоречивыми. Список литературы 1. Sebastian H.-J., Intelligent support systems, Proceedings of EUFIT’93 (Sept. 7-10, 1993, Aachen, Germany) 299-307. 2. Язенин А.В. Методы оптимизации и принятия решений при нечетких данных: Дис… докт. физ.-матем. наук: ТГУ - Тверь, 1995. 3. Wang Xizhao, Ha Minghu. Note on maxmin m/E estimation // Fuzzy Sets and Systems. 1998, №94, pp. 71-75. 4. Язенин А.В. К задаче максимизации возможности достижения нечеткой цели// Изв. АН РФ. Теория и системы управления. - 1999. - №4. - С. 120-123. 5. Гольштейн Е.Г, Юдин Д.Б. Новые направления в линейном программировании. - М., Сов. радио. - 1966. |
http://swsys.ru/index.php?id=823&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Компьютер - хранитель домашнего очага
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- ДИНАМИКА-2 - программа для решения осесимметричных и плоских задач
- Инженерная программа трехмерного моделирования магнитных систем LittleMag

 "I и AiÎP(G).
"I и AiÎP(G).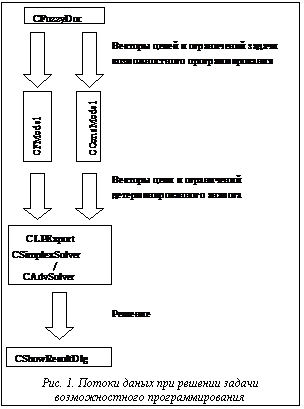 При восстановлении распределения пользователь определяет, какого типа распределение нужно восстанавливать – распределение с конечным носителем (триангулярное) или с бесконечным (нормальное) и вводит выборку экспертных значений. Система восстанавливает параметры распределения и устанавливает распределение соответствующего параметра задачи.
При восстановлении распределения пользователь определяет, какого типа распределение нужно восстанавливать – распределение с конечным носителем (триангулярное) или с бесконечным (нормальное) и вводит выборку экспертных значений. Система восстанавливает параметры распределения и устанавливает распределение соответствующего параметра задачи.
 Процесс решения задачи начинается с генерации модели задачи. Пользователь последовательно выбирает модель критерия задачи, указывает ее размерность (число переменных, целевых функций и ограничений), задает модели и названия ограничений.
Процесс решения задачи начинается с генерации модели задачи. Пользователь последовательно выбирает модель критерия задачи, указывает ее размерность (число переменных, целевых функций и ограничений), задает модели и названия ограничений.