Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Задача распознавания динамически изменяющихся образов: постановка и пути решения
Аннотация:
Abstract:
| Авторы: Дли М.И. (midli@mail.ru) - Филиал Московского энергетического института (технического университета) в г. Смоленске (профессор, зам. директора по научной работе), г. Смоленск, Россия, доктор технических наук, Гимаров В.А. (feu@sci.smolensk.ru) - Смоленский филиал Московского энергетического института (технического университета), г. Смоленск, Россия, доктор экономических наук, Гимаров В.В. (feu@sci.smolensk.ru) - Смоленский филиал Московского энергетического института (технического университета), г. Смоленск, Россия, доктор экономических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 13230 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
Задача распознавания образов в своей классической постановке достаточно давно и хорошо изучена. Ее основной особенностью является неизменность во времени классов (образов) распознавания. Между тем более естественной представляется ситуация, когда данные классы являются динамически изменяющимися, то есть когда они эволюционируют во времени, поэтому существенная проблема, возникающая при распознавании образов, – это их изменчивость. Имеется множество причин этой изменчивости. Во-первых, существует изменчивость, связанная с процессом измерения. Каждый датчик порождает аддитивный и/или мультипликативный шум; шум квантования возникает в процессе дискретизации. Систематические ошибки измерения не приводят к возникновению изменчивости при условии, что искажения всегда одинаковы. На практике, однако, иногда применяются датчики со всевозможными искажениями в различных рабочих диапазонах, что приводит к возникновению изменчивости. Вторым источником изменчивости могут быть шум или искажения, вносимые каналами связи или промежуточными элементами обработки, разделяющими источник информации и измерительную систему. Труднее всего поддается описанию третья составляющая изменчивости, свойственная собственно образам: объекты, принадлежащие одному классу (скажем, все различные варианты буквы А), могут очень сильно отличаться друг от друга. Этот вид изменчивости существенно зависит от характера образа. Отметим, что абсолютное значение изменчивости каждого из образов (собственная изменчивость) имеет значение лишь в сравнении с различиями, существующими между образами, относящимися к разным классам (межклассовая изменчивость). Отмеченная изменчивость может иметь как статический, так и динамический характер. Под статической будем понимать изменчивость, статистические характеристики которой не изменяются во времени. Динамическая же изменчивость предполагает изменение во времени усредненных (по множеству объектов) характеристик. Данная изменчивость, приводящая к понятию динамически изменяющихся образов, надо сказать, в литературе в достаточной степени не отражена, хотя, несомненно, широко распространена на практике.
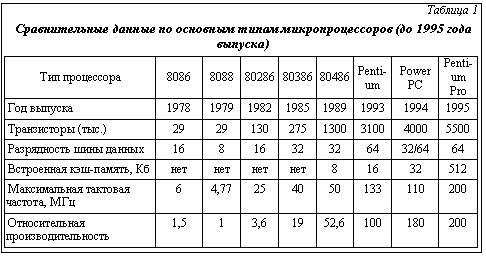
Приведем примеры подобных образов. Пример 1. Пусть в качестве эталонов совокупности образов рассматривается группа похожих между собой людей, а в качестве множества объектов, относящихся к данным образам, – множество их различных фотографий. Очевидно, с течением времени образы и, соответственно, их эталоны изменяются (люди стареют). Если в такой ситуации не учитывать временную (динамическую) изменчивость образов и, например, провести опознавание (распознавание) 60-летних людей по их фотографиям, сделанным в 18-летнем возрасте, легко допустить многочисленные ошибки. Пример 2. Мутация биологических объектов: грибы-мутанты. Несколько лет назад в отечественных средствах массовой информации стали появляться сообщения о ядовитых грибах-мутантах, вызывавших смертельные отравления собравших и употребивших их в пищу грибников. Более детальные исследования показали, что на самом деле речь идет об обыкновенных ядовитых грибах типа бледных поганок, отличительные признаки которых по каким-то причинам, возможно, вследствие перемены климата изменились так, что данные грибы стали практически неотличимыми от съедобных. Ясно, что в данном случае динамически изменяющимися являются образы определенных ядовитых грибов. Пример 3. Тенденция развития микропроцессоров для персональных компьютеров (ПК). Приведем фрагмент таблицы 1, иллюстрирующей эволюцию микропроцессоров фирмы Intel. Если рассматривать совокупность всех типов микропроцессоров для ПК, выпускаемых всевозможными фирмами, как множество различных объектов, характеризуемых признаками типа приведенных в таблице 1, то можно определить на данном множестве, например, три образа: S1 – наилучшие (микропроцессоры), S2 – среднего класса, S3 – низкого класса, и считать эталоном класса микропроцессоры именно фирмы Intel (хотя, конечно, это несколько спорное предположение), то, как нетрудно видеть из приведенных данных, образ S1 с течением времени весьма заметно изменяется. Перечень подобных примеров легко продолжить, но уже и на основании приведенных можно сделать вывод, что задача динамического распознавания возникает всегда, когда множество распознаваемых объектов рассматривается как некоторая популяция, развивающаяся во времени. Укажем, что с формальной стороны в классической постановке задача распознавания образов задается четверкой: {X,S,D(x),R}, где X – признаковое (выборочное) пространство; n – размерность признакового пространства (количество признаков, характеризующих распознаваемые объекты); D(x) – множество решающих правил, по которым осуществляется отнесение распознаваемого объекта к тому или иному образу;
Отсутствие в этой четверке одного из первых трех элементов определяет тип задачи распознавания: 1) задано множество классов или образов 2) заданы множество классов 3) задано пространство признаков X; требуется найти множество С учетом временной изменчивости образов ясно, что решающее правило должно быть функцией не только признаков, но и времени, то есть
Обзор основных известных методов распознавания образов [2-6] позволил выделить наиболее перспективные для возможного решения этой задачи подходы (см. табл. 2). Следующим шагом в данном направлении, очевидно, должна стать разработка новых или адаптация известных методов таким образом, чтобы они могли использоваться для распознавания образов, изменяющихся во времени. Список литературы 1. Дьяконов В.П. Компьютер в быту. - Смоленск: Русич, 1996. 2. Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Метод потенциальных функций в теории обучающих машин. - М.: Наука, 1970. 3. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. - Новосибирск: Изд-во ин-та математики, 1999. 4. Фукунага К. Введение в статистическую теорию распознавания образов. - М.: Наука, 1979. 5. Дли М.И., Круглов В.В., Осокин М.В. Локально-аппроксимационные модели социально-экономических систем. - М.: Физматлит, 2000. 6. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и гибридные нейронные сети. - М.: Физматлит, 2001. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=838&page=article |
Версия для печати Выпуск в формате PDF (1.18Мб) |
| Статья опубликована в выпуске журнала № 3 за 2001 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Электронный глоссарий
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Опыт разработки и эксплуатации системы управления базами данных (DBS/R)
- Анализ отечественного опыта и структуризация механизмов управления оборонным научно-промышленным комплексом
- Использование матричных квадродеревьев для хранения площадных картографических объектов
Назад, к списку статей



 Под динамически изменяющимся будем понимать образ, характеристики которого изменяются во времени. Информативным представителем подобного образа может служить его некий усредненный по множеству объектов (относящихся к данному образу) в произвольный момент времени эталон, характеристики которого будут, естественно, зависеть от момента усреднения.
Под динамически изменяющимся будем понимать образ, характеристики которого изменяются во времени. Информативным представителем подобного образа может служить его некий усредненный по множеству объектов (относящихся к данному образу) в произвольный момент времени эталон, характеристики которого будут, естественно, зависеть от момента усреднения. – множество распознаваемых образов (классов), называемое иногда алфавитом;
– множество распознаваемых образов (классов), называемое иногда алфавитом; – риск потерь при распознавании.
– риск потерь при распознавании. (это множество обычно задается обучающей выборкой) и пространство признаков X; требуется найти решающее правило D(x), минимизирующее риск R;
(это множество обычно задается обучающей выборкой) и пространство признаков X; требуется найти решающее правило D(x), минимизирующее риск R;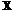 , которая минимизировала бы величину R;
, которая минимизировала бы величину R; .
.