Новый подход к проблеме коллективного выбора на базе удовлетворения взаимных требований сторон
| Андрейчикова О.Н. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Индивидуальный выбор иногда определяется не только предпочтениями лица, принимающего решение (ЛПР), но и требованиями, которые предъявляются альтернативами к выбирающей стороне. Примерами могут служить задачи выбора спутника жизни, выбор производственных партнеров для предприятия, квартирный обмен, поиск применения новому химическому соединению или техническому устройству и т.д. Такие задачи будем называть задачами с двухсторонними требованиями. На практике задачи принятия решений (ЗПР) с двухсторонними требованиями часто сводят к традиционным задачам путем добавления критериев, характеризующих требования выбираемых альтернатив. Например, все технические системы предъявляют определенные требования к условиям их эксплуатации, которые в традиционных задачах учитываются с помощью критериев эксплуатационные свойства, устойчивость к механическим повреждениям и т.п. Высокие оценки по критериям такого типа соответствуют низким требованиям альтернатив к ЛПР и наоборот. Весьма распространенным является подход, когда требования выбираемой стороны учитываются в форме ограничений, накладываемых на параметры задачи. Так, подбирая банк для обслуживания предприятия, требования банка к величине основных фондов предприятия учитываются в форме ограничения на рассматриваемые альтернативы. Если требования банка к размеру основных фондов не выполняются, то эта альтернатива отвергается. Сведение двухсторонних задач к традиционным постановкам приводит к отсеиванию альтернатив, предъявляющих высокие требования к выбирающей стороне. Такой подход правомерен в случае предъявления невыполнимых требований. Однако если выбирающая сторона располагает ресурсами для совершенствования, то не следует отвергать альтернативы, к нему побуждающие. Например, при проектировании виброзащитных систем для транспортных средств пневматический гаситель колебаний часто отвергается из-за низкой устойчивости к механическим повреждениям, хотя он обладает высоким качеством виброзащиты, хорошей технологичностью, энергетическими и стоимостными характеристиками. Обеспечение защиты от возможных повреждений (например установка защитного кожуха) может сделать эту альтернативу оптимальной. Для решения двухсторонних ЗПР предлагается новый подход, в котором объекты (выбирающие и выбираемые) описываются наборами свойств и требований. Удовлетворение требований оценивается с помощью вычисляемых мер сходства. Задача бинарного синтеза (подбор пары объектов, наилучшим образом удовлетворяющих требованиям друг друга) решается на основе выбранного принципа компромисса. Распределение объектов двух различных множеств по парам, обладающее определенными свойствами, рассматривается в многокритериальной задаче о назначениях. Задачи, которые исследуются в данной работе, отличаются тем, что 1) результатом является не «лучшее распределение назначений (пар)», а выявление одной или нескольких лучших пар; 2) новый объект может формироваться из элементов двух и более множеств. Пусть A={A1, A2, …, An} и B={B1, B2, …, Bm} – множества объектов, из которых нужно синтезировать новый объект AB. Каждый из объектов Ai, i=1, …, n и Bj, j=1, …, m описывается набором свойств PAi, PBj и набором требований RAi, RBj. Информация о свойствах и требованиях объектов может быть представлена дескрипторами, количественными оценками и нечеткими множествами. Для каждого из объектов множества B объекты множества A можно упорядочить на основе меры сходства предъявляемых требований RBj со свойствами конкретных объектов PAi, i=1,…, n. В свою очередь, каждый из объектов Ai предъявляет свои требования к объекту Bj. Свойства объектов могут выражаться лингвистическими или числовыми оценками. Лингвистическим оценкам могут соответствовать наименования или нечеткие множества. Требования могут формулироваться в виде равенств или неравенств, например PAik=RBjk; PAik£RBjk; PAik³RBjk; Необходимо найти объекты ABlÎA´B, l=1,…,nm, для которых оценка удовлетворения взаимных требований является максимальной. Для получения интегральной оценки, характеризующей степень удовлетворения требованиям, необходимо перейти к безразмерным и соизмеримым величинам. В качестве таких величин будем использовать меры сходства, которые по-разному вычисляются для количественных и качественных оценок и для требований различного вида [1,2]. Если требования выражены равенствами и заданы в виде количественных оценок, то степень их совпадения со свойствами по k-му критерию можно оценить с помощью следующих мер сходства:
При лингвистическом описании символьные строки либо совпадают, либо нет, при этом сходство по k-му критерию для требований любого вида оценивается по двухбалльной шкале Sk(RBj, PAi) = Если RBjk и PAik представляют собой нечеткие множества, соответствующие лингвистическим оценкам, скалярный индекс сходства можно вычислить по формуле Жаккара [3]:
где операция |X| обозначает скалярную мощность нечеткого множества X, заданного на базовом множестве U: Удовлетворение требований, сформулированных в виде неравенств PAik£RBjk (PAik³RBjk) для количественных оценок можно оценивать с помощью меры включения PAik в RBjk:
Если требования сформулированы в виде Для нечетких оценок используется скалярный индекс частичного совпадения
Формирование обобщенной оценки является двухэтапной процедурой, которая может выполняться различными способами в зависимости от используемых принципов оптимальности. Один из этапов связан с вычислением обобщенной оценки удовлетворения требований каждого объекта по множеству критериев, другой этап заключается в построении оценки степени взаимного удовлетворения требований для пары объектов Ai и Bj. Для построения обобщенных оценок предложены целевые функции на основе принципа гарантированного результата, принципа справедливого компромисса и принципа равномерной оптимальности. Выполнение разных требований может иметь неодинаковую важность для выбирающей стороны, в связи с чем в формулах используются нормированные весовые коэффициенты. Аддитивная целевая функция:
где wk и vk – нормированные весовые коэффициенты критериев, по которым производится сравнение; Kl =m(RAiÈPBj), Kz =m(RBjÈPAi) – мощности объединений множеств сравниваемых свойств и требований. Следует отметить, что размерности наборов требований свойств могут различаться. В таких случаях сравнение можно производить либо по пересечению этих множеств, исключая из рассмотрения несовпадающие элементы, либо принять следующее соглашение: если требование RAik задано, а соответствующее свойство PBjk нет, то Sk(RAi,PBj)=0; если для заданного свойства PBjk не задано соответствующее требование RAik, то Sk(RAi,PBj)=1. Применение принципа равномерной оптимальности может привести к тому, что будет выбрана пара, в которой требования одной стороны учтены полностью, а требования другой стороны проигнорированы. Главным преимуществом аддитивных функций является высокая вероятность получения непустого выбора. Аддитивно-мультипликативная целевая функция:
Эта функция допускает компенсацию значений удовлетворения требований по разным критериям, но не допускает компенсации оценок в паре. При использовании такой функций выбор может оказаться пустым только в том случае, если требования одной из сторон полностью не удовлетворены. Мультипликативная целевая функция:
Эта функция не допускает компенсации оценок ни по критериям, ни в паре. Главным недостатком такой функции является высокая вероятность пустого выбора. Максиминная целевая функция:
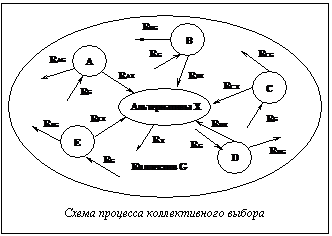
где знак Предложенный подход к решению ЗПР с двухсторонними требованиями можно применить для разрешения конфликтов, возникающих в процессах коллективного принятия решений. При этом двухсторонняя задача становится многосторонней. Схема процесса коллективного выбора показана на рисунке. Участниками выбора являются объекты A, B, C, D, E, вместе составляющие коллектив G. У каждого участника существует свой набор требований к выбираемым альтернативам RAX, RBX и т.д. Со стороны альтернатив также могут существовать определенные требования к выбирающей стороне RX. Кроме того, каждый участник имеет требования к коллективу RAG, RBG, …, REG, а коллектив предъявляет требования к участникам RG. Каждый элемент из множества альтернатив X={X1, X2, …, Xn} описывается набором свойств PXi, i=1, …, n и набором требований к выбирающей стороне RXi. Всякий участник процесса выбора характеризуется набором свойств PA, PB, PC, PD, PE и имеет собственный набор требований к альтернативам. Кроме того, каждый участник может иметь определенные требования к коллективу. Множество участников процесса выбора обозначим Y={Y1, Y2, …, Ym}, свойства участников PYj, j=1, …, m; а требования к альтернативам и к коллективу RYjX и RYjG соответственно. Рассмотрим ситуации, которые могут возникать в процессе коллективного выбора. 1. Требования всех ЛПР объединяются (требования к одним и тем же свойствам пересекаются) и используются для ранжирования множества заданных альтернатив X в соответствии с выбранным принципом оптимальности. При этом могут быть установлены различные весовые коэффициенты и для критериев, и для участников выбора. ЗПР может решаться с учетом или без учета требований альтернатив RX.
где RY =RY1ÈRY2È…ÈRYm, PY = PY1ÈPY2È … ÈPYm, Kl=m(RYÈPXi), Kz=m(RXiÈPY), wk, vk – весовые коэффициенты требований коллектива Y и альтернатив X. Если существует альтернатива, удовлетворяющая объединенным требованиям, то ЗПР можно считать решенной. Без учета требований альтернатив аддитивная целевая функция имеет вид:
Если выбран другой принцип оптимальности, в качестве F5 применяются функции вида F2 – F4. 2. Если не существует альтернативы, которая устраивает всех участников, то на базе объединенных требований RY формируется представление о такой альтернативе, осуществляется ее поиск и добавление к множеству X, после чего задача решается еще раз при измененном составе множества X. 3. Если невозможно найти альтернативу, отвечающую требованиям всех ЛПР, то имеет место конфликтная ситуация, для разрешения которой можно использовать разные способы. Способ 1. Для каждого ЛПР решается задача выбора лучшей альтернативы, при этом можно учитывать или не учитывать требования выбираемой стороны. Принцип оптимальности и конкретный вид целевой функции выбирается по согласованию с участниками процесса. При выборе аддитивной целевой функции с учетом требований альтернатив получим следующий набор решений:
Выбор X*Yj = 0 только в том случае, если ни одно из требований сторон не выполняется. На основании полученных результатов проводится кластеризация множества участников. Пусть X*Yj =Xi, тогда к классу Hq будут отнесены все участники Yj, для которых выполняется условие "YjÎHq | X*Yj =Xi, j=1, …, m. Во всех сформированных классах Hq, q=1, …, Q производится объединение свойств и требований участников, а затем задача решается еще раз с новым множеством участников H=H1ÈH2È … ÈHQ, в роли которых теперь выступают коалиции (кластеры). Кластеризация может проводиться неоднократно до тех пор, пока множество классов не перестанет уменьшаться. Анализ выявленных классов позволяет выявить конфликтующие требования и неудовлетворительные качества объектов. На следующем шаге устанавливается по- рог D (0£D£1), который используется для формирования отношений сходства Главными источниками конфликта являются бескомпромиссные требования к альтернативам, имеющим слабое сходство. Разрешение конфликта в этом случае возможно на основе информации, представленной в виде требований и возможных уступок коллективу. Под уступкой здесь подразумевается готовность ЛПР отказаться от бескомпромиссного требования и предел приемлемого для него значения. За уступку ЛПР может потребовать компенсации, в качестве которых могут быть изменение атрибутов других требований к альтернативам, добавление, исключение таких требований, а также выдвижение требований, не касающихся альтернатив. Например, соглашаясь на среднюю прибыль вместо высокой, ЛПР может выдвинуть условие получения места в совете директоров кооперативного предприятия. Набор таких требований вместе с выбранной альтернативой представляет собой результаты решения задачи. Таким образом, процесс разрешения конфликта является итерационной процедурой, в ходе которой могут неоднократно изменяться требования участников к выбираемым альтернативам и весовые коэффициенты требований, а также выдвигаться требования различных компенсаций, являющихся платой за компромисс. При свертке индивидуальных предпочтений ЛПР может быть выбран способ вычисления коллективного пред- почтения (дикторский, утилитарный, эгалитар- ный [4]). Если участники процесса выбора не могут достичь консенсуса, то производится усечение исходного множества Y либо путем отделения несогласных от устойчивой коалиции (ядра), либо дроблением на несколько коалиций. Включение в рассмотрение требований со стороны альтернатив привносит дополнительную информацию для примирения или разделения участников процесса выбора. Способ 2. Этот способ отличается от первого алгоритмом разрешения конфликта. На первом этапе выявляется сходство требований ЛПР к альтернативам и на основе полученных результатов определяются коалиции участников. Затем определяется тип коллективного предпочтения и проводится анализ требований участников к коллективу RYjG и RG. То есть если в первом способе результаты решения ЗПР используются для формирования классов, то во втором ЗПР решается после достижения компромисса (высокой степени сходства) в требованиях ЛПР к альтернативам. Если в результате изменения исходных требований удается прийти к разрешению конфликта, то выявляется лучшая альтернатива, которая будет приемлемой для всех. Если такой альтернативы нет, производится ее поиск. В случае непреодолимых противоречий изменяется состав множества участников Y. Список литературы 1. Андреев В.Л. Классификационные построения в экологии и систематике. – М.: Наука, 1980. - 142 с. 2. Андрейчиков А.В., Андрейчикова О.Н. Компьютерная поддержка изобретательства (методы, системы, примеры применения). – М.: Машиностроение, 1998. - 476 с. 3. Нечеткие множества и теория возможностей. Последние достижения. – М.: Радио и связь, 1986. - 408 с. 4. Мулен Э. Кооперативное принятие решений: Аксиомы и модели. – М.: Мир, 1991. - 464 с. |
http://swsys.ru/index.php?id=841&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Разработка загрузчика программного обеспечения встроенной системы управления
- О программной реализации геоинформационных систем
- Алгоритмы и программное обеспечение системы обработки топопланов
- Зарубежные базы данных по программным средствам вычислительной техники
- Формирование программ развития больших систем административно-организационного управления

 , где k – индекс соответствующего критерия, по которому производится сравнение свойства с требованием.
, где k – индекс соответствующего критерия, по которому производится сравнение свойства с требованием.
 .
.

 .
. Если требование удовлетворяется, значение меры включения равно 1, в противном случае 0
Если требование удовлетворяется, значение меры включения равно 1, в противном случае 0
 .
. .
. ,
, .
. .
. ,
, может означать либо сумму, либо произведение. Максиминный подход характеризуется весьма высокой вероятностью пустого выбора.
может означать либо сумму, либо произведение. Максиминный подход характеризуется весьма высокой вероятностью пустого выбора. ,
,
 .
. .
.
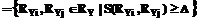 . Анализ отношений сходства позволяет определить близкие и сильно отличающиеся требования, которые в дальнейшем могут быть скорректированы. Одним из способов является изменение весовых коэффициентов требований.
. Анализ отношений сходства позволяет определить близкие и сильно отличающиеся требования, которые в дальнейшем могут быть скорректированы. Одним из способов является изменение весовых коэффициентов требований.