Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Групповая сборка мусора в системах реального времени
Аннотация:
Abstract:
| Автор: Данилов М.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10812 |
Версия для печати Выпуск в формате PDF (1.49Мб) |
Многие современные системы программирования используют механизм сборки мусора. Применение этого механизма обеспечивает преимущества, которые, в частности, делают желательным его использование в системах реального времени (СРВ). Одним из препятствий использования сборки мусора в СРВ является низкая эффективность планирования приложения реального времени из-за продолжительного блокирования высокоприоритетных задач сборщиком мусора. В данной статье рассматривается групповая сборка мусора – новый подход к организации сборки мусора в СРВ, позволяющий в ряде случаев в несколько раз сократить продолжительность интервалов блокирования прикладных задач. Динамическое управление памятью. В системах с динамическим управлением памятью блоки памяти для размещения динамически формируемых программных объектов выделяются из специально зарезервированных в системе ресурсов: динамических областей памяти (ДОП). По завершении работы с динамическим объектом выделенная под него память возвращается системе и тем самым становится доступной для дальнейшего использования. Свойства системы с динамическим управлением памятью во многом определяют способ возвращения динамической памяти. Многие системы программирования предоставляют приложениям средства только явного возвращения динамической памяти. Это означает, что прикладная программа в некоторой точке выполнения должна явно, посредством соответствующего вызова, вернуть системе освободившийся блок памяти. Требование явного возвращения памяти влечет много проблем, таких как увеличение объема кода приложения и внесение ограничений в его структуру. Кроме того, такой подход часто приводит к ошибкам типа утечки памяти и обращения к несуществующим объектам. Подобные проблемы отсутствуют в системах с автоматическим возвращением динамической памяти. В системах, реализующих этот механизм, локализация объектов, не используемых приложениями, и возвращение занимаемых ими ресурсов производится автоматически, то есть на системном уровне. Автоматическое возвращение памяти зачастую имеет меньшие накладные расходы, чем явное [1]. Ненужные, неиспользуемые более объекты называются мусором, соответственно, системная задача, осуществляющая поиск мусора и возвращение памяти, называется сборщиком мусора, а реализуемый ею процесс – сборкой мусора (СМ). Этапы СМ. Процесс СМ можно условно разбить на два этапа: обнаружение мусора и возвращение занимаемой им памяти. Техника возвращения памяти варьируется в различных алгоритмах СМ, в то время как способ обнаружения мусора является общим для большинства современных алгоритмов. Алгоритм обнаружения мусора обычно определяется в терминах корневого множества (КМ) и графа достижимости объектов. В момент начала СМ считается, что все элементы КМ используются прикладными задачами. КМ обычно составляют глобальные и статические переменные, локальные переменные, расположенные в стековом пространстве, и объекты, находящиеся в регистрах процессора. Далее в пошаговом режиме строится граф достижимости объектов ДОП из КМ. После построения графа принимается, что все входящие в него динамические объекты используются прикладными задачами. Прочие объекты считаются мусором. Возвращение занимаемой мусором памяти часто заключается только в том, что она помечается как свободная и пригодная для повторного использования. Однако существует ряд перемещающих алгоритмов СМ. Алгоритмы СМ этого класса предусматривают перемещение расположенных в ДОП объектов, что позволяет предотвратить фрагментацию свободной памяти. Неделимые и инкрементальные алгоритмы СМ. Простейшие алгоритмы СМ неделимы (stop-and-collect) – весь цикл СМ представляет собой процедуру, исключающую выполнение прикладных задач. Неделимые алгоритмы отличает максимальная простота и производительность. Низкие накладные расходы на сборщиков мусора данного класса определяются отсутствием переключений контекста между системной и прикладными задачами. Кроме того, на протяжении всего времени работы сборщика мусора граф достижимости динамических объектов не подвергается изменениям, то есть не возникает необходимости осуществлять какую-либо синхронизацию действий сборщика мусора и прикладных задач. Неделимые алгоритмы подходят для использования в пакетных системах, для которых важна производительность и отсутствуют требования своевременности реакции на внешние события. В системах, где приостановка выполнения всех задач на время выполнения полного цикла СМ недопустима, используют инкрементные алгоритмы. Работа инкрементных сборщиков мусора представляет собой не одну неделимую операцию, а последовательность небольших по времени квантов, чередующихся с выполнением прикладных задач. При этом возникает проблема, состоящая в том, что между двумя соседними квантами работы сборщика мусора прикладные задачи могут производить изменения в графе достижимости динамических объектов. Поэтому необходимо предусматривать возможность сохранения информации о подобных изменениях с последующей коррекцией внутренних структур данных. Для согласования работы приложений и сборщика мусора необходимо выполнять синхронизирующие операции, роль таких операций выполняют барьеры [2]. Барьеры представляют собой дополнительные инструкции к выполняемым прикладными задачами операциям над указателями. Еще один источник издержек – появляющийся мусор (floating garbage). Суть проблемы заключается в том, что некоторые объекты, уже помеченные инкрементным сборщиком мусора как используемые, становятся недостижимыми вследствие действий приложения. Таким образом, за счет увеличения накладных расходов на СМ инкрементные алгоритмы значительно расширяют область применения систем с автоматическим возвращением памяти. СМ в СРВ. Критерий эффективности механизма СМ во многом определяется спецификой требований к прикладным программам. Так, для большинства вычислительных систем под эффективностью понимают высокую производительность. В СРВ производительность является необходимой составляющей эффективности, но не достаточной. Не менее важна степень влияния СМ на время выполнения прикладных задач. Алгоритм СМ для СРВ должен гарантировать только небольшие и ограниченные задержки выполнения прикладных задач. В СРВ обычно используется вытесняющее планирование, основанное на фиксированных приоритетах задач. В этом случае сборщик мусора можно представить задачей с максимальным приоритетом, на время работы которой блокируется выполнение всех прикладных задач [3]. Как правило, в СРВ используются инкрементные алгоритмы СМ. Проблема со сборщиками мусора реального времени определяется относительностью понятия небольшой задержки. Что для ряда приложений является приемлемым, то для приложений другого класса недопустимо. Хорошим критерием применимости алгоритма СМ в конкретной системе является успешный исход анализа выполнимости. С точки зрения анализа выполнимости поведение каждой i-й задачи характеризуется тремя параметрами: Тi – период задачи, Сi – время выполнения задачи и Di – относительный срок выполнения задачи. Приоритет прикладной задачи выбирается с учетом значений этих параметров. Сборщик мусора – задача с максимальным приоритетом – также характеризуется периодом (ТGC) и временем выполнения (CGC). Анализ выполнимости заключается в нахождении времени отклика (R) прикладных задач реального времени. Время отклика вычисляется по формуле:
где hp(i) – множество задач с приоритетами большими, чем приоритет i-й задачи. Приложение считается выполнимым, если время отклика каждой задачи не превышает относительного срока выполнения. Как видно из формулы, желательно, чтобы сборщик мусора запускался как можно реже и каждый раз работал как можно меньше. Важным показателем качества алгоритма СМ для СРВ является время, необходимое для сканирования КМ. Проблема заключается в том, что элементы КМ – наиболее часто используемые объекты, и использование барьеров при доступе к ним приводит к неоправданно большим накладным расходам. Поэтому операция сканирования КМ обычно выполняется как атомарная, что часто является основным ограничением на уменьшение продолжительности (времени выполнения) кванта работы сборщика мусора. СМ оказывает большое влияние на реактивность системы и время выполнения высокоприоритетных задач [4,5]. Работа с графом достижимости требует синхронизации со всеми прикладными задачами. В этом случае тело сборщика мусора представляет собой одну сплошную критическую секцию. По этой причине сборщику мусора назначается максимальный приоритет. Однако назначению сборщику мусора временных параметров, соответствующих максимальному приоритету, часто мешает ряд ограничений, например, время сканирования КМ. При этом проявляется инверсия приоритетов [6], которая значительно снижает эффективность планирования. Однако продолжительность инверсии приоритетов неоправданно велика. Действительно, выполнение высокоприоритетной задачи откладывается, в том числе и на время СМ, создаваемого низкоприоритетной задачей, в общем случае не имеющей к высокоприоритетной никакого отношения. СМ, основанная на приоритетах. Назначение сборщику мусора максимального приоритета фактически означает применение синхронизирующего протокола невытесняемых критических секций (ПНКС). Согласно этому протоколу на время работы с разделяемым ресурсом задача объявляется невытесняемой, что равносильно назначению ей максимального приоритета. Достоинство ПНКС заключается в его простоте, недостаток – в большой продолжительности инверсии приоритетов. Значительно меньшую продолжительность инверсии приоритетов обеспечивают более гибкие протоколы синхронизации, основанные на понятии порогового приоритета [7], например, протокол превентивного наследования приоритетов (ППНП). Суть протокола ППНП заключается в том, что каждому ресурсу ставится в соответствие некий параметр – пороговый приоритет ресурса. Пороговый приоритет ресурса равен высшему приоритету задачи из числа задач, использующих этот ресурс. Приоритет задачи, занимающей ресурс, повышается (на все время выполнения критической секции) до уровня порогового приоритета данного ресурса. Применительно к предмету рассмотрения это означает, что для большей эффективности работы системы в каждый момент времени приоритет сборщика мусора должен определяться пороговым приоритетом собираемого мусора. Действительно, динамический объект потенциально может быть достижим из элементов КМ, принадлежащих различным задачам, при этом некоторые объекты ДОП являются разделяемыми ресурсами. СМ в соответствии с протоколом превентивного наследования – вариант экстремальный. С одной стороны, он обеспечивает высокую эффективность планирования многозадачного приложения, с другой стороны, объем информации, необходимой для определения приоритета сборщика мусора, очень велик. Каждый динамический объект рассматривается как потенциально разделяемый ресурс, то есть каждому объекту или группе объектов должен ставиться в соответствие пороговый приоритет. Последнее обстоятельство также обязывает выполнять достаточно трудоемкий анализ кодов прикладных задач с целью определения круга задач, потенциально имеющих доступ к динамическим объектам. В связи с большими накладными расходами следует признать СМ в соответствии с ППНП подходом с ограниченным кругом применения. Предлагаемый ниже протокол защиты разделяемых ресурсов, использующий дополнительную информацию о структуре многозадачного приложения реального времени, позволяет уменьшить продолжительность инверсии приоритетов при сохранении объема информации на приемлемом уровне. Группы логически связанных задач. Приложение реального времени традиционно представляется в виде множества задач T={t1,t2,...,tn}. Его также можно рассматривать как множество групп задач G={g1,g2,...,gm}, где каждая группа суть множество логически связанных задач реального времени [8]. Причем группы не пересекаются, каждая задача может входить в состав только одной группы, а задачи из разных групп независимы. Требования групп к аппаратным ресурсам системы определяют затраты процессорного времени, необходимого для решения каждой задачи в отдельности, и требования к оперативной памяти. Причем требования к памяти формулируются скорее для группы в целом, чем для каждой задачи в отдельности. Задачи могут совместно использовать динамические структуры данных. Поэтому рассмотрение требований прикладных задач к объему памяти в отдельности может привести к пессимистической оценке общего количества памяти, необходимой для корректной работы приложения в целом. Протокол локально невытесняемых критических секций (ПЛНКС). Суть предлагаемого протокола заключается в том, что задача, занимающая разделяемый ресурс, становится невытесняемой локально, то есть невытесняемой прикладными задачами, входящими в одну с ней группу. Необходимый эффект может быть достигнут за счет введения нового параметра – локального порогового приоритета группы (g), численно равного высшему приоритету задачи, входящей в эту группу:
Приоритет задачи, занимающей ресурс, повышается (на все время выполнения критической секции) до уровня локального порогового приоритета группы, элементом которой она является. По своим характеристикам, таким как эффективность планирования и накладные расходы на реализацию, ПЛНКС занимает промежуточное положение между оригинальным ПНКС и ППНП. ПЛНКС обеспечивает меньшую эффективность планирования, чем ППНП. Однако он также позволяет значительно уменьшить эффект инверсии приоритетов, при этом накладные расходы на организацию СМ остаются на уровне, приемлемом для большинства приложений. Групповая СМ. Суть предлагаемого подхода к реализации СМ в СРВ характеризуется двумя основными положениями. Во-первых, процедура СМ выполняется для каждой группы в отдельности. Во-вторых, приоритет сборщика мусора устанавливается равным ceilg+1, где ceilg – локальный пороговый приоритет соответствующей группы. При этом прикладные задачи на приоритетной шкале раздвигаются, освобождая приоритетные уровни для сборщика мусора. Число задач, выполняющих СМ (число сборщиков мусора), определяется количеством групп в системе. Каждый i-й сборщик мусора характеризуется периодом (ТiGC) и временем выполнения (CiGC). При такой постановке задачи формула для вычисления времени отклика прикладной задачи приобретает вид:
В случае, когда сборщики мусора имеют не максимальный приоритет в системе, для них также становится актуальным анализ выполнимости. При этом относительный срок выполнения сборщика мусора принимается равным его периоду. Тогда
Предлагаемый подход обеспечивает повышение эффективности планирования СМ для СРВ. За счет незначительного увеличения объема информации о структуре многозадачного приложения и соответствующего увеличения накладных расходов достигается уменьшение продолжительности инверсии приоритетов. Действительно, как видно из формулы (4), выполнение высокоприоритетной задачи откладывается теперь только на время, необходимое для СМ, созданного задачами, входящими в состав групп, чей локальный пороговый приоритет больше приоритета данной задачи. Активная работа прочих задач с объектами, расположенными в ДОП, теперь не влияет на время отклика высокоприоритетной задачи. Разбиение приложения на группы логически связанных задач определяет разбиение КМ на подмножества, сканировать которые можно независимо. Возможность разбиения процесса сканирования КМ без установки барьеров на его элементы значительно расширяет область, в рамках которой производится выбор временных параметров сборщика мусора. Рассмотрим на примере, как использование групповой СМ позволяет добиться выполнимости многозадачного приложения реального времени, невыполнимого в случае назначения сборщику мусора максимального приоритета.
В дополнение к повышению эффективности планирования переход к групповой СМ также способствует повышению надежности и гибкости системы. Повышение надежности. В системах, в которых величина кванта СМ определяется временем сканирования КМ, особенно важным становится получение точного значения времени сканирования в худшем случае, которое определяется максимально возможным размером КМ. Если в ходе работы системы какая-либо задача превысит свой лимит на размер КМ, это может привести к увеличению времени сканирования КМ сверх запланированного значения и, как следствие, к нарушению временных ограничений других задач. Переход к СМ для каждой группы в отдельности позволяет снизить область распространения ошибок такого рода за счет разделения времени сканирования КМ и разнесения процесса СМ по различным приоритетным уровням. В ряде случаев целесообразным является выделение отдельной ДОП для каждой группы. Суммарный размер множества ДОП не будет превышать размера единой, так как требования к памяти различных групп задач независимы по определению. Необходимость поддерживать несколько ДОП одновременно [9] может окупиться повышением отказоустойчивости всей системы. Действительно, соблюдение всех сроков выполнения прикладных задач гарантируется только в том случае, если на этапе разработки системы требования к оперативной памяти были сформулированы реалистично, без оптимизма. Если в ходе работы системы с одной ДОП какая-либо задача превысит свой лимит на используемый объем памяти, это может привести к нехватке памяти для всех задач в системе. Дефицит динамически выделяемой памяти может привести к нарушению временных ограничений прикладных задач. Разделение одной ДОП на несколько ограничивает область распространения ошибок такого рода пределами одной группы. Повышение гибкости. Идея раздельной СМ открывает еще одну полезную возможность – для разных частей приложения можно собирать мусор по-разному, то есть с использованием различных алгоритмов. Эта возможность актуальна для неоднородных приложений реального времени. Допустим, что к задачам реального времени добавлена фоновая задача без временных ограничений и с требованием большого количества вычислительных ресурсов. Использование единой инкрементной стратегии СМ для всего приложения приведет к низкой эффективности использования процессорного времени. Большую эффективность может обеспечить решение об использовании инкрементного алгоритма СМ для задач реального времени и неделимого алгоритма СМ для фоновой активности. Следует заметить, что для организации СМ по различным алгоритмам не требуется разделения ДОП на несколько самостоятельных подобластей. В случае выделения отдельной ДОП для каждой группы также возможно использование различных дисциплин выделения памяти в разных ДОП. Так, для обслуживания задач с повышенными требованиями к надежности может использоваться специальная дисциплина управления динамической памятью с блоками фиксированного размера. В этом случае некоторое снижение эффективности использования памяти окупается повышением предсказуемости механизма управления памятью. Список литературы 1. Wilson P.R. Uniprocessor garbage collection techniques. Technical report, University of Texas at Austin, 1994. 2. Wilson P.R., Johnstone M.S. Real-time non-copying garbage collection. Technical report, University of Texas at Austin, 1993. 3. Kim T., Chang N., Kim N., Shin H. Scheduling Garbage Collector for Embedded Real-Time Systems. Technical report, Seoul National University. 4. The real-time specification for Java. http://www.rtj.org. 5. International J consortium specification. Real-time Core extensions. www.j-consortium.org. 6. Никифоров В.В., Данилов М.В. Статическая обработка спецификаций программных систем реального времени. //Программные продукты и системы.- 2000.- №4.- С.13-18. 7. Henriksson R. Scheduling garbage collection in embedded systems. Lund, 1998. 8. Nilsen K., Lee S. PERC real-time API. NewMonics Inc., 1997. 9. Wilson P.R., Johnstone M.S., Neely N., Boles D. Dynamic storage allocation: a survey and critical review. Technical report, University of Texas at Austin, 1995. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=855&page=article |
Версия для печати Выпуск в формате PDF (1.49Мб) |
| Статья опубликована в выпуске журнала № 4 за 2001 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Методы восстановления пропусков в массивах данных
- Потоковый анализ программ, управляемый знаниями
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- Системы компьютерной поддержки процессов анализа, синтеза и планирования решений в условиях неопределенности
- Зарубежные базы данных по программным средствам вычислительной техники
Назад, к списку статей



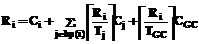 , (1)
, (1) . (2)
. (2)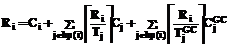 . (3)
. (3) (4)
(4)
 Приложение реального времени представляет собой две группы (g1 и g2), состоящие из трех задач (t1, t2, t3). Временные параметры задач приведены в таблице 1. Группы g1 и g2 вносят разный вклад во время выполнения сборщика мусора 1 и 2 соответственно, причем квант сборщика мусора не может быть уменьшен из-за требования неделимости операции сканирования КМ. Распределение приоритетов и расчет времени отклика задач (см. табл. 2) показывают, что в случае назначения сборщику мусора максимального приоритета прикладная задача t1 не укладывается в установленные сроки выполнения (D
Приложение реального времени представляет собой две группы (g1 и g2), состоящие из трех задач (t1, t2, t3). Временные параметры задач приведены в таблице 1. Группы g1 и g2 вносят разный вклад во время выполнения сборщика мусора 1 и 2 соответственно, причем квант сборщика мусора не может быть уменьшен из-за требования неделимости операции сканирования КМ. Распределение приоритетов и расчет времени отклика задач (см. табл. 2) показывают, что в случае назначения сборщику мусора максимального приоритета прикладная задача t1 не укладывается в установленные сроки выполнения (D
 В соответствии с групповой СМ необходимо выделить две задачи для СМ, по одной на каждую группу (см. табл. 3). Сборщик мусора группы g1 (GC1) получает максимальный приоритет. Сборщику мусора группы g2 (GC2) назначается приоритет в соответствии с локальным пороговым приоритетом второй группы, на приоритетной шкале GC2 будет располагаться между задачами t1 и t3 (см. табл. 4). Расчет времени отклика показывает, что все задачи, включая сборщики мусора, выполняются в установленные сроки.
В соответствии с групповой СМ необходимо выделить две задачи для СМ, по одной на каждую группу (см. табл. 3). Сборщик мусора группы g1 (GC1) получает максимальный приоритет. Сборщику мусора группы g2 (GC2) назначается приоритет в соответствии с локальным пороговым приоритетом второй группы, на приоритетной шкале GC2 будет располагаться между задачами t1 и t3 (см. табл. 4). Расчет времени отклика показывает, что все задачи, включая сборщики мусора, выполняются в установленные сроки.