Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование адаптации в алгоритмах синтеза топологии электронных систем
Аннотация:
Abstract:
| Авторы: Курейчик В.М. (kur@tgn.sfedu.ru) - Таганрогский технологический институт Южного федерального университета (профессор), Таганрог, Россия, доктор технических наук, Мухлаев А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11120 |
Версия для печати Выпуск в формате PDF (1.53Мб) |
Термин адаптация известен из биологии как приспособление организма к изменению внешних условий [I]. Наблюдения в области адаптации живых организмов привели к идее наделить указанным свойством технические системы, комплексы программ и т.д. Подразумевается, что такие адаптивные объекты создают предпосылки гибкости при решении задач, а также используют накапливаемый в процессе работы опыт для повышения целесообразности своего функционирования. Как правило, под адаптивной понимают систему, которая работает при наличии частичной (или полной) априорной неопределенности и при изменяющихся внешних условиях, а получаемую в процессе работы информацию об этих условиях использует для повышения эффективности работы. Адаптация является неотъемлемым качеством интеллекта, а мышление человека - это высшая форма приспособительного процесса [I]. Так как в качестве перспективных направлений развития информационных систем выделяются интеллектуализация и интеграция, то качество адаптивности должно быть присуще и интеллектуализированным техническим системам, в частности системам автоматизированного проектирования (САПР). То есть интеллектуализация САПР должна привести к качественно новому уровню организации САПР с присущим интеллектуальным системам свойством адаптации. При этом адаптивными связями должны быть затронуты все компоненты интеллектуальной САПР: пакеты прикладных программ решения конструкторских задач, база знаний, система логического вывода, диалоговый интерфейс и т.д. Общепризнано, что высшим проявлением интеллекта (как естественного, так и искусственного) является творчество, связанное, в частности, с проблемой выбора [2], которая, в свою очередь, во многом определяется способностью эффективной адаптации. Рассматривая адаптацию в САПР как в сложной системе, состоящей из четырех основных компонентов (комплекса технических средств (КТС), комплекса программных средств (КПС), объекта проектирования (ОП) и пользователя (П)), остановимся на адаптации КПС к ОП, которая означает способность САПР приспосабливаться к потоку ОП в изменяющихся условиях с целью достижения оптимального проектирования на основе поступающей априорной и апостериорной информации.
Интересом же данного изложения будет служить апостериорная адаптация, которая применяется при полном отсутствии или скудости априорной адаптации. Известна классификация ПА в зависимости от свойств объекта адаптации [2]. Модифицируя известную классификацию, получаем дополнен- ную (рис. 2).
Будем рассматривать АА САПР в условиях априорной неопределенности, то есть когда трудно заранее что-либо сказать о предпочте- нии той или иной из имеющихся альтернатив- ных структур. Отметим, что когда существует возможность заранее определить оптимальную из альтернатив, естественно, необходимо воспользоваться такой информацией. Но во многих реальных ситуациях провести такой анализ невозможно. В этом случае как раз и применя- ется АА, позволяющая некоторым образом компенсировать недостаток априорной информации и реализовать эффективную стратегию управления. Рассмотрим возможность применения методов АА в САПР конструкторского этапа проектирования микроэлектронной аппаратуры. Как известно, наблюдается рост доли программного обеспечения в САПР, а вместе с ним в современных САПР растет доля альтернативного математического и программного обеспечения. В связи с этим на некоторых этапах проектирования встает задача динамического выбора одного из имеющихся множеств альтернативных алгоритмов, методик, правил и т.д. Указанная проблема может требовать решения, например, на этапах: - компоновки для адаптивного выбора одного из методов начального разрезания графа, моделирующего схему; - размещения для адаптивного выбора одной из альтернативных итерационных процедур его улучшения; - ранжирования соединений перед трассировкой (выбор одной из альтернативных методик упорядочения соединений) и т.д. Итак, имеется A={ai,a2,...,an} альтернативных вариантов решения задачи. Необходимо в условиях априорной неопределенности в каждый из моментов времени t=1.2 выбрать для решения задачи Zi один из вариантов aj Î A таким образом, чтобы экстремизировать среднюю величину показателей качества получаемых решений FS = Задачи АА решаются либо с помощью стохастических [3], либо с помощью детерминированных алгоритмов [4]. Стохастическим алгоритмам присущи некоторые недостатки: необходимость применения датчика случайных чисел, равномерно распределенных на отрезке [0;1] для реализации метода деления отрезка, а также сложность подбора параметров, которые существенным образом влияют на скорость сходимости алгоритмов. На основании изложенного рассмотрим применение моделей, разработанных в [4] для обеспечения выбора альтернативных вариантов в конструкторских САПР, и покажем, что с некоторыми модификациями они позволяют эффективно решать практические задачи при достаточно простой реализации. Алгоритм адаптивного упорядочения соединений перед трассировкой Процесс трассировки сверхбольших интегральных схем (СБИС), как правило, разбивается на 2 этапа: упорядочение трассируемых соединений и собственно трассировка. При этом главной целью предварительного упорядочения является создание наиболее благоприятных условий для последующей трассировки. Как правило, при упорядочении соединений пользуются тактиками, основанными на длине соединений [5], на количестве "чужих" контактов, охваченных описывающим прямоугольником трассируемого соединения [6], динамическими методами [5] и т.д. Статистические исследования показывают, что перечисленные методики приводят приблизительно к одинаковым результатам трассировки при большом числе решаемых задач разных типов, размерности и т.п. При этом априори нельзя отдать предпочтение какой-либо из методик упорядочения для решения конкретной задачи. Отсюда ясно, что наиболее приемлемой методикой упорядочения была бы возможность использования одного из нескольких вариантов в каждом конкретном случае. Следовательно, целесообразным представляется использование методов АА для динамического выбора одной из методик. Схема процесса АА показана на рисунке 3. Постановка задачи АА для заданной задачи такова. Пусть имеется n альтернативных алгоритмов упорядочения соединений перед трассировкой (п=3, A1 – длинные-короткие, А2 – короткие-длинные, А3 – упорядочение по Айресу). Необходимо для решения каждой из потока задач динамически выбирать один из алгоритмов Ai таким образом, чтобы обеспечить экстремизацию Автомат адаптации Для решения поставленной задачи будем использовать модифицированный детерминированный алгоритм, предложенный в [5]. Автомат А представляет собой четвертку: A={S,A,B,F}, где S= {S11,S12,…,S1m;S21,S22,…S2m…; …;Sn1,Sn2,…,Snm} – множество внутренних состояний автомата; m – глубина памяти автомата; F=||fij|| – матрица переходов. A={a1,a2,...,an} – множество действий автомата; В= {0,1} – множество входов автомата, причем "0" соответствует выигрышу, а "1" проигрышу автомата. Будем считать, что в нашем случае каждому из действий автомата соответствует та или иная методика упорядочения соединений.
В [4] исследуется поведение автоматов с линейной тактикой в стационарных и переключаемых случайных средах. Если рассматривать поток задач x1, x2, ..., хk на проектирование как переключаемую случайную среду, p(p1, p2,..., рn), где p1, p2,..., рn – смысл вероятности удачного применения альтернативы ai для решения задачи xj, то фундаментальные результаты, полученные в [4], применимы для решения поставленной задачи. Указывается, в частности, что математическое ожидание выигрыша, которое необходимо максимизировать, достигает максимума при некотором конечном значении емкости памяти m. Оптимальное значение m подбирается исходя из средней частоты переключения случайных сред и свойств самих сред. Ввиду того, что средняя частота переключения сред для задачи упорядочения соединений лежит в пределах 0,03: 0,3, а также учитывая полную априорную неопределенность в предпочтении какой-либо из альтернатив упорядочения, получаем из [5] оптимальную глубину памяти автомата, в нашем случае m=2. Граф-схема автомата для трех указанных альтернатив и матрицы переходов приведена на рисунке 4. При этом состояниям S11, S12 соответствует применение действия a1 (упорядочение длинные-короткие), состояниям S21, S22 действие а2 (упорядочение короткие-длинные), состояниям S31, S32 действие а3 (упорядочение по Айресу). Отметим, что в случае проигрыша переход к альтернативному действию (группе состояний) осуществляется к той группе состояний, которая имеет наибольшую среднюю оценку по сравнению с остальными. Так, если автомат адаптации находился в состоянии S12 и последовал проигрыш, то на следующем шаге автомат перейдет в состояние с максимальной средней оценкой, то есть либо к S11, если Методика оценки бинарных потерь Рассчитаем относительный показатель, который назовем коэффициентом выигрыша при применении i-й альтернативы Fi= Естественно, чем ближе значение Fi к 1, тем выше качество упорядочения соединений. Так как процесс адаптации происходит на потоке задач, то возможен подсчет для каждой из альтернатив среднего значения коэффициента выигрыша В таком случае естественно считать выигрышем при применении альтернативы аi и решении задачи xk выполнение условия: "Fj; Fi – Таким образом, предлагаемая методика формирования входов автомата В=[0,1] стимулирует динамическое отслеживание и своевременный переход к тем альтернативам, текущие значения эффективности которых превышают средние статистические для остальных альтернатив. Экспериментальные исследования пакета прикладных программ (ППП) адаптации ППП адаптации разработан в соответствии с принципами структурного программирования и включает в себя четыре основных модуля. В зависимости от исходных данных управляющим программным модулем инициируются те или иные шаги задания, то есть монитор определяет состав и последовательность выполнения программных модулей. Модуль OCEN.EXE в соответствии с предложенной методикой АА осуществляет оценку бинарных потерь по конечному результату проектирования (трассировке). Модуль ADA.EXE моделирует автомат целесообразного поведения. Информацию о бинарных потерях ADA.EXE получает от OCEN.EXE через DD.DAT. Через файл DD.DAT также может производиться настройка ADA.EXE. Можно задавать параметр N=1,2,3,4, что соответствует глубине памяти автомата целесообразного поведения и А=1,2,...,10, где А – число обрабатываемых альтернатив. Отметим, что разработано две модификации модуля OCEN.EXE: модуль OCENR.EXE и модуль OCENT.EXE. Первый служит для оценки бинарных потерь на этапе размещения, а второй – на этапе упорядочения соединений. Модуль ADA.EXE управляет вызовом альтернативы для работы над следующим проектом. Осуществляется это также через файл DD.DAT путем указания параметра АА – номера работающей альтернативы. Эта информация обрабатывается модулем вызова указанной в файле DD.DAT альтернативы – VIB.EXE. Этот модуль вызывает для работы альтернативу, номер которой указан в данный момент в файле DD.DAT. ППП адаптации содержит альтернативные модули по упорядочению соединений и альтернативные модули по итерационному размещению. Так, модуль UP1.ЕХЕ производит упорядочение соединения по принципу короткие-длинные; UP2.EXE – длинные-короткие; UPA.EXE – в соответствии с правилом Айреса. Для этапа размещения разработан модуль RAZM.EXE. Его многоальтернативность обеспечивается передачей ему параметра АА из файла DD.DAT. Причем параметр АА может принимать целочисленные значения, равные 2,3,4,5, что будет соответствовать 2-х, 3-х, 4-х, 5-и перестановочным алгоритмам итерационного улучшения размещения. Отметим, что работа указанных программ адаптации осуществлялся в автоматическом режиме, хотя пользователь также может управлять этим процессом, принудительно задавая параметры файла DD.DAT. На основании экспериментальных исследований видно, что преимущество адаптивного метода становится заметным после n > 20, то есть когда накапливается информация, на основе которой можно ввести адаптивный выбор. Таким образом, логично сделать вывод об эффективности адаптивного упорядочения соединений на этапе упорядочения соединений перед трассировкой. В заключение отметим, что предложенный в работе метод организации адаптивных программ, решающих задачу адаптивного выбора, может быть использован не только для процедуры упорядочения соединений перед трассировкой, но и для других процедур топологического синтеза. Методика же адаптивного упорядочения соединений реализована в виде ППП простой структуры для IBM-совместимых ЭВМ объемом около 270 Кб. Экспериментальные исследования доказали эффективность предложенного метода. Так, средняя суммарная длина соединений проектируемых объектов сократилась до 10%, а число реализованных соединений увеличилось на 5-7%. Список литературы 1. Норенков И.П., Маничев В.Б. Основы теории проектирования САПР: Учеб. для втузов.-М.: Высш. шк., 1990. - 335 с. 2. Holland J.H. Adaptation in Natural and Artificial Systems. An Introductory Analysis with Application to Biology, Control, and Artificial Intelligence. University of Michigan, 1975, 210р. 3. Курейчик В.М. Генетические алгоритмы. Монография. - Таганрог: Изд-во ТРТУ, 1998. - 242 с. 4. Цетлин М.Л. Исследования по теории автоматов и моделирование биологических систем. - М.: Наука, 1969. - 316 с. 5. Курейчик В.М. Математическое обеспечение КТП с применением САПР. - М.: Радио и связь, 1990. - 351 с. 6. Weste N., Eshraghaian К.. Principles of CMOS VLSI Design - A system perspective. Addison -Westey 1992. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=888&page=article |
Версия для печати Выпуск в формате PDF (1.53Мб) |
| Статья опубликована в выпуске журнала № 3 за 2000 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Комплекс автоматизированного проектирования геотехнических сооружений "КАППА"
- Потоковый анализ программ, управляемый знаниями
- Разработка загрузчика программного обеспечения встроенной системы управления
- О программной реализации геоинформационных систем
Назад, к списку статей



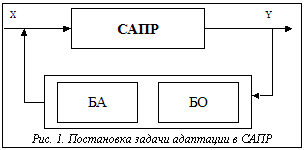 Интерпретируя известную постановку задачи адаптации для систем автоматического управления (САУ) [2], получаем постановку задачи адаптации для САПР. Объектом управления в указанном случае будет служить САПР, а адаптивным регулятором – специальная подсистема адапта- ции (рис. 1). Пусть каждое получаемое решение при этом динамически оценивается в блоке оце- нок (БО). Задача адаптации состоит в том, чтобы сформировать в блоке адаптации (БА) последовательность воздействий, экстремизирующих показатели качества Q(Y) получаемых решений (критерии адаптации), то есть Q(Y) ®
Интерпретируя известную постановку задачи адаптации для систем автоматического управления (САУ) [2], получаем постановку задачи адаптации для САПР. Объектом управления в указанном случае будет служить САПР, а адаптивным регулятором – специальная подсистема адапта- ции (рис. 1). Пусть каждое получаемое решение при этом динамически оценивается в блоке оце- нок (БО). Задача адаптации состоит в том, чтобы сформировать в блоке адаптации (БА) последовательность воздействий, экстремизирующих показатели качества Q(Y) получаемых решений (критерии адаптации), то есть Q(Y) ® , где W – область допустимых управлений.
, где W – область допустимых управлений.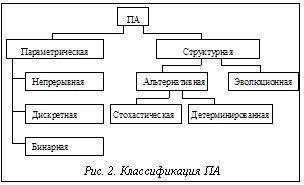 Остановимся на методе альтернативной адаптации (АА), которая применяется в случае нескольких альтернативных вариантов структур объекта адаптации путем динамического выбора какой-либо из имеющихся структур.
Остановимся на методе альтернативной адаптации (АА), которая применяется в случае нескольких альтернативных вариантов структур объекта адаптации путем динамического выбора какой-либо из имеющихся структур. , где fk – показатель качества решения задачи Zk , полученного в момент времени tk.
, где fk – показатель качества решения задачи Zk , полученного в момент времени tk.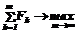 , где Fk – показатель качества решения, полученного для задачи Хk.
, где Fk – показатель качества решения, полученного для задачи Хk.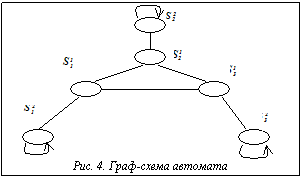 Входы В определяются результатами применения какого-либо из действий: удачное применение –"1", неудачное – "0" (случай бинарных потерь [3]).
Входы В определяются результатами применения какого-либо из действий: удачное применение –"1", неудачное – "0" (случай бинарных потерь [3]).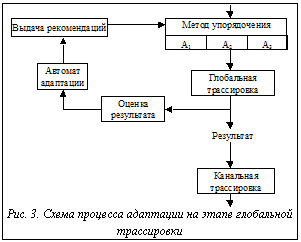 Укажем также, что в зависимости от входного сигнала автомат изменяет внутреннее состояние, которое, в свою очередь, определяет действие, применяемое автоматом в следующий дискретный момент времени ti, t=l,2,... . Матрица переходов F=|| fij || определяет зависимость между предыдущим состоянием автомата и последующим, при этом
Укажем также, что в зависимости от входного сигнала автомат изменяет внутреннее состояние, которое, в свою очередь, определяет действие, применяемое автоматом в следующий дискретный момент времени ti, t=l,2,... . Матрица переходов F=|| fij || определяет зависимость между предыдущим состоянием автомата и последующим, при этом  носит смысл вероятности перехода автомата из состояния Ski(t) в состояние Ski(t+1). В нашем детерминированном случае fij={0,1}. Так как В={0,1}, то достаточно задать F1=||fij|| и F2=|| fij(1)||.
носит смысл вероятности перехода автомата из состояния Ski(t) в состояние Ski(t+1). В нашем детерминированном случае fij={0,1}. Так как В={0,1}, то достаточно задать F1=||fij|| и F2=|| fij(1)||. , или к S13, если
, или к S13, если  . Физический смысл оценок Fi станет ясен ниже.
. Физический смысл оценок Fi станет ясен ниже. .
. , где k – число задач, решавшихся с помощью ai.
, где k – число задач, решавшихся с помощью ai. <0, где j=l,2,...,n, то есть В=1; i¹j; n – число альтернатив. А проигрышем – истинность следующего условия: "Fj; Fi –
<0, где j=l,2,...,n, то есть В=1; i¹j; n – число альтернатив. А проигрышем – истинность следующего условия: "Fj; Fi –