Авторитетность издания
Добавить в закладки
Следующий номер на сайте
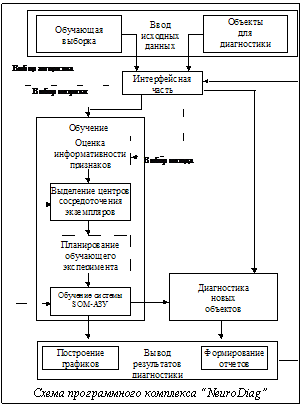
Программный комплекс нейросетевой диагностики
Аннотация:
Abstract:
| Авторы: Субботин С.А. (subbotin@zntu.edu.ua) - Запорожский национальный технический университет, Запорожье, Украина, доктор технических наук, Дубровин В.И. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 12580 |
Версия для печати Выпуск в формате PDF (1.53Мб) |
В последнее время отечественная промышленность понимает необходимость внедрения систем качества, соответствующих стандартам ISO 9000. Однако эти стандарты являются завершающим этапом развития, и чтобы построить такие современные системы качества, необходимо избавиться от такого серьезного недостатка, как высокий уровень дефектности. Эффективным средством против этого недостатка является диагностика процессов и изделий [1]. В большинстве диагностических программ используются статистические методы [2-7], которые требуют, чтобы объем обучающей выборки был достаточно велик. Если же размер обучающей выборки мал (когда из-за уникальности или дороговизны изделий и сложности испытаний невозможно или нежелательно проводить большое количество экспериментов), статистические и эвристические алгоритмы, как правило, не позволяют решать задачу классификации с необходимой достоверностью. Кроме того, эти системы не обладают самоорганизацией и не способны помочь пользователю в планировании эксперимента. Программный комплекс “NeuroDiag” осуществляет диагностику на основе альтернативной и сравнительно новой методики нейронных сетей (НС). Одним из важнейших свойств НС является способность к аппроксимации многомерных функций, что позволяет использовать их для моделирования сложных процессов и объектов. Не менее важное свойство НС – обучаемость – дает возможность строить на их основе адаптивные системы. Благодаря этому НС могут применяться в задачах классификации. В качестве базовой модели НС в программном комплексе “NeuroDiag” выбрана НС с латеральным торможением – Карта признаков самоорганизации Кохонена (Self-Organizing Map – SOM), применение которой для решения задачи классификации в условиях малого размера обучающей выборки весьма перспективно [8]. SOM является НС с латеральным торможением [9] и относится к классификаторам, для обучения которых используются выборки образов с заранее незаданной классификацией. При обучении НС предъявляются входные векторы без указания желаемых выходов и корректируются веса согласно алгоритму, предложенному Теуво Кохоненом [10]. Если число входных векторов в обучающем множестве велико по отношению к выбранному числу кластеров, то после обучения веса сети будут определять центры кластеров, распределенные в пространстве входов таким образом, что функция плотности этих центров будет аппроксимировать функцию плотности вероятности входных векторов. Кроме того, веса будут организованы таким образом, что топологически близкие узлы будут соответствовать физически близким (в смысле евклидова расстояния) входным векторам. SOM способны классифицировать экземпляры по степени близости их признаков. Это позволяет применять их для выделения центров сосредоточения экземпляров, что может быть использовано при планировании обучающего эксперимента, когда большое количество опытов ставить затруднительно, например, по причине дороговизны или уникальности изделий. Планирование обучающего эксперимента в этом случае производится следующим образом: на основании значений признаков всех экземпляров обучающей выборки формируется SOM, а затем для экземпляров, которые наиболее близки к сформированным векторным центрам SOM, проводятся эксперименты по определению фактических классов [8].
Результаты классификации SOM могут быть наделены фактическим смыслом путем постановки в соответствие номеру каждого узла SOM номера того фактического класса, к которому относится большая часть экземпляров обучающей выборки, отнесенных SOM к данному узлу [8]. Для этого может быть использовано ассоциативное запоминающее устройство (АЗУ). Постановка соответствия производится путем записи пары (кортежа) <номер узла SOM, номер класса> в АЗУ. В качестве АЗУ может быть использован как блок линейной, или динамической памяти, обслуживаемый соответствующей процедурой, так и нейросетевая ассоциативная память [9]: а) для системы с двумя классами – однослойный дискретный перцептрон [9,11]; б) для системы с большим числом классов – многослойная НС или комбинация ассоциативной памяти на основе НС Хопфилда [9,11] с нейросетевым селектором максимума. Блок SOM-АЗУ может быть рекомендован для использования в системах классификации, когда: а) реальный принцип деления экземпляров на классы совпадает или близок к методу классификации SOM; б) размер обучающей выборки, то есть совокупности значений признаков экземпляров и сопоставленных им номеров классов недостаточен для классификации другими методами (статистическими, нейросетевыми), а экземпляры одного и того же класса имеют близкие значения признаков, то есть классы хорошо разделяются и имеют центры, вокруг которых достаточно плотно сосредоточены экземпляры, относящиеся к данному классу. Комбинация НС SOM и нейросетевого АЗУ является ядром данного программного комплекса. В основу обучения и работы системы SOM-АЗУ положены алгоритмы: · формирования SOM; · SOM-классификации; · подбора метрики SOM; · оценки информативности признаков; · обучения нейросетевого АЗУ на основе однослойного перцептрона: · обучения нейросетевого АЗУ на основе НС Хопфилда: - проекционный (псевдоинверсный) алгоритм обучения, - итерационный проекционный (псевдоинверсный) алгоритм обучения, - алгоритм обучения нейросетевого селектора максимума; · обучения системы SOM-АЗУ; · классификации SOM-АЗУ. В процессе формирования SOM для разделения экземпляров по кластерам в качестве меры близости используется метрика Минковского:
где N – количество признаков; xis – значение i-го признака s-го экземпляра; wji – i-я компонента векторного центра wj={wj1,wj2,...,wjN}T; λ – показатель степени; dj – расстояние между j-м узлом SOM и вектором признаков s-го экземпляра. Изменяя λ, можно получить неограниченное число других метрик. Однако на практике следует ограничиваться легко вычислимыми метриками, топологически близкими к фактическому разделению классов. Очевидно, чем ближе выбранная метрика к реальной закономерности разделения на классы, тем точнее и с меньшими потерями будет производиться классификация. Для систем диагностики возникает задача автоматического выбора наилучшей метрики из множества заданных для каждого конкретного набора классов изделий. Эта задача решается в данном программном комплексе с помощью специально разработанного алгоритма итеративного подбора метрики [8]. Рассмотренные метрики, как правило, предполагают, что все признаки, по которым производится классификация, являются одинаково значимыми. Однако на практике признаки разделяются на значимые и незначимые. В отношении некоторых признаков заранее известно или предполагается, что они являются наиболее или наименее значимыми, но степень такой значимости точно неизвестна и не позволяет производить классификацию только на основе данного признака или исключить данный признак в случае его малозначимости. Если использовать такую априорную информацию при обучении НС, то очевидно, что классификация изделий будет производиться с меньшим числом ошибок. Алгоритмы оценки информативности признаков [8] позволяют решать эту задачу с помощью данного программного комплекса, реализованного на языке Object Pascal интегрированной среды разработчика Inprise (Borland) Delphi 5.0 и функционирующего под управлением Windows-95/98 и Windows-NT 4.0. Для проверки работоспособности и оценки применимости “NeuroDiag” проводились эксперименты по решению задач распознавания (классификации) объектов, диагностики и прогнозирования состояния сложных технических процессов и объектов. Эксперименты показали, что программный комплекс успешно справляется с данными задачами, затрачивая на их решение сравнительно небольшое количество времени. Результаты экспериментов позволяют рекомендовать разработанный программный комплекс для решения прикладных задач технической диагностики. Универсальность – важное свойство НС – позволяет применять “NeuroDiag” при решении ряда задач медицинской диагностики, в социологии, экономике, экологии и в других областях. Список литературы 1. Дубровин В.И. Идентификация и оптимизация сложных технических процессов и объектов.-Запорожье: ЗГТУ, 1997.-92 с. 2. Дубровин В.И., Луценко Д.В., Степаненко А.А. Диагностический программный комплекс //Информационный листок № 01–99.– РГАСНТИ 50.41.25. - Запорожский ЦНТЭИ, 1999. 3. Дубровiн В., Степаненко О., Луценко Д. Діагностика процессів та керування якістю // Досвід розробки і застосування САПР в мікроелектрониці /Матеріали п’ятої міжнародної науково-технічної конференції CADSM’99. – Львів, Державний університет “Львівська політехніка”, 1999. - С.22-24. 4. Внуков Ю.Н., Дубровин В.И. Методики прогнозирования с использованием теории статистических оценок и статистической классификации //Высокие технологии в машиностроении /Матер. VI междунар. науч.-тех. сем. - Харьков: ХГПУ,1996. - С.26-27. 5. Внуков Ю.Н., Дубровин В.И., Алгоритм классификации с использованием дискриминантных функций //Высокие технологии в машиностроении /Сб. науч. тр. ХГПУ.-Харьков: ХГПУ, 1998. - С.64-66. 6. Дубровин В.И., Корецкий Н.Х. Об одном подходе к прогнозированию надежности изделия //Электронное моделирование, 1986. - Т.8. - № 6, ноябрь-декабрь. -С.97-98. 7. Дубровин В.И. Эвристические алгоритмы классификации//Машиностроитель, 1998. - №7. - С. 6-9. 8. Дубровин В.И., Субботин С.А. Построение адаптивных систем диагностики на основе нейронных сетей с латеральным торможением // Радіоелектроніка. Інформатика. Управління, 1999. - № 2. - С. 110 -114 9. Нейрокомпьютеры и интеллектуальные роботы / Под ред. Амосова Н.М.-Киев: Наукова думка, 1991.-272 с. 10. Kohonen T. Self-organization and associative memory.-Berlin: Springer, 1984.-255 p. 11. Neural Network Toolbox User Guide / Beale M., Demuth H.-Natick: Mathworks, 1997.-700 p. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=891&page=article |
Версия для печати Выпуск в формате PDF (1.53Мб) |
| Статья опубликована в выпуске журнала № 3 за 2000 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формирование программ развития больших систем административно-организационного управления
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Метод интегрированного описания топологических отношений в геоинформационных системах
- Опыт разработки и эксплуатации системы управления базами данных (DBS/R)
- Механизм контроля качества программного обеспечения оптико-электронных систем контроля
Назад, к списку статей



 Важно отметить, что при классификации с помощью SOM номер узла, к которому отнесен экземпляр, и фактический номер его класса в общем случае не совпадают: разделяя экземпляры, SOM производит субъективную классификацию, не имеющую того реального физического смысла, которым мы наделяем классы.
Важно отметить, что при классификации с помощью SOM номер узла, к которому отнесен экземпляр, и фактический номер его класса в общем случае не совпадают: разделяя экземпляры, SOM производит субъективную классификацию, не имеющую того реального физического смысла, которым мы наделяем классы. , λÎR,
, λÎR,