Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Интерактивная процедура построения модели тренда для экономических показателей
Аннотация:
Abstract:
| Авторы: Виноградов Г.П. (wgp272ng@mail.ru) - Тверской государственный технический университет (профессор), Тверь, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 20359 |
Версия для печати Выпуск в формате PDF (1.53Мб) |
При решении задачи прогнозирования рядов динамики экономических показателей, например с помощью MS Excel, необходимо учитывать следующие их особенности. 1. Анализируемый экономический показатель Y испытывает на себе влияние множества факторов X={xi, i= 2. Важной особенностью временных рядов экономических показателей является то, что «вклад» в тенденцию Y(ti-p) с ростом p уменьшается. Это позволяет утверждать, что временной ряд практически любого экономического показателя является объектом с конечной памятью SP. Очевидно, что величина p будет определять объем выборки, принимаемой во внимание при расчете параметров модели. В зависимости от шага дискретизации временной ряд задается таблицей вида Dn={y(ti), i= 3. Наличие данных, резко отличающихся от трендовых значений (выбросов). Выявление внешних факторов, вызывающих выброс, позволяет построить сценарий при ответе на вопрос «что будет, если…». Эти особенности делают проблематичным качество прогноза на основе модели тренда, полученной по методу наименьших квадратов, в том числе и с весовыми коэффициентами. Больший эффект в таких ситуациях дает сочетание опыта и знаний пользователя и возможностей статистических методов, реализованных в соответствующих программных продуктах по схеме, представленной на рисунке1. Предлагаемая схема основывается на предположении, что для экономических показателей можно предложить множество вариантов аппроксимации закона распределения, удовлетворяющих статистическим правилам проверки их адекватности. Выбор конкретного варианта будет определяться, очевидно, знанием причинно-следственных связей между входными факторами и анализируемым показателем, которые имеются на качественном уровне у опытного пользователя.
где m – количество значений временного ряда Y, W={wi,i= Варьируемыми параметрами при минимизации данного функционала будут: весовые коэффициенты wi, i= Качество модели, описывающей тренд, можно отобразить такими показателями, как величина остаточной дисперсии, значение критерия Фишера, величина отклонения в контрольных точках, величина остаточной дисперсии в точках, в которых наблюдается всплеск и др. Поэтому задачу выбора оптимальных параметров и структуры модели тенденции в общем случае надо рассматривать как задачу многокритериальной оптимизации. Пусть описанные выше показатели качества построенной модели тенденции образуют вектор Z={zj, j= Будем предполагать, что ЛПР обладает достаточно высокой квалификацией и опытом, то есть его шкала ценностей определена таким образом, что различные наборы показателей Z={zj, j= Z(W(1)) Z(W(1)) ~Z(W(2))ÛU(Z(W(1)))=U(Z(W(2))), где W(1),W(2)Î WW (здесь WW – множество допустимых значений управляющих переменных, в данном случае весовых коэффициентов). Сделанное предположение относительно функции U(Z(W)) позволяет определить решение задачи векторной оптимизации как множество точек Для найденных значений W0ÎWW должно выполняться условие оптимальности по Парето и поиск решения должен проходить по паретовой границе множества Z(W): E(Z(W))={Z(1) Î Z(W), Z(1) Функция U(Z(W)) в явном виде, как правило, неизвестна, поэтому для определения оптимальных величин целесообразно использовать интерактивные процедуры. Для этого выбирается некоторое решение W(1) с использованием информации, получаемой от ЛПР, определяется поведение U(Z(W(0))) в окрестности точки W(1) и на этой основе строится последовательность решений {W(l)}, которая при определенных условиях сходит- ся к W0. Однако часто множество E(Z(W)) невыпуклое и поиск в пространстве решений сопряжен со значительными трудностями. Поэтому паретову границу целесообразно параметризировать элементами более простого множества A. Из известных процедур параметризации для целей оптимизации прогностических свойств модели тенденции наиболее подходящей является процедура ассортиментной параметризации, базирующаяся на теореме Карлина [1]: U(Z(W))=U(a,Z(W))=, где <·> – скалярное произведение; aÎA, {aj³0, 1. " WÎПW, $a(W)ÎA:W(a)=arg max U(a(W), Z(W)) =W0. 2. "aÎA, $W(a)ÎПW, где PW – область Парето. Пусть V* – совокупность предпочтительных с точки зрения ЛПР показателей Z(W), причем V*¹Æ и V*ÎE(Z(W)), тогда согласно принятой процедуре параметризации V* можно представить как V*=s(A*), где A* – множество максимальных элементов отношения Тогда задача принятия решения по выбору оптимальных структуры и параметров модели тренда временного ряда может быть записана в виде: U*(a)®max, aÎA, (1) где U*=U*s. Таким образом, произведена параметрическая декомпозиция экстремальной задачи U(Z(W)), WÎWW, Z(W)ÎWZ на задачу вычисления s и задачу maxU(s(a)), aÎA. Такая декомпозиция распределяет роли в человеко-машинном диалоге следующим образом: · на ЭВМ вычисляется параметризация s, которая для ассортиментной параметризации имеет вид maxY при Z(W)³aZ; · ЛПР участвует в решении задачи оптимизации (1).
В качестве формальной основы диалоговой процедуры построения модели тренда можно воспользоваться как градиентными методами решения, так и методами прямого поиска, не требующими информации о производных целевой функции. Как известно, градиентные методы более эффективны, что имеет большое значение в случае участия ЛПР в выполнении алгоритма. Однако в силу того что модель имеет стохастический характер, латентными факторами выступают качественные признаки и, кроме того, функция U(·) предпочтений ЛПР в общем случае не является дифференцируемой, классические методы градиентного поиска и их модификации не могут считаться приемлемыми. Наибольший эффект следует ожидать от применения методов случайного поиска. При организации диалога с ЛПР использовалась следующая модель реакции ЛПР на предъявленное решение. По двум решениям Z(W(1)) и Z(W(2)) ЛПР сообщает вектор с компонентами: xi i=
Общая структура алгоритма случайного поиска для задачи построения модели тренда временного ряда имеет следующий вид: a(S+1)=a(S)+ +J(S+1), где S – номер обращения к ЛПР; J(S+1) – вариация вектора a (определяется в пространстве случайных векторов в зависимости от модели реакции ЛПР). При x i = 0 вариацию ai следует положить равной 0. В остальных случаях целесообразно использовать алгоритм с поощрением случайностью: Ji(S+1)= где g(S+1) – скаляр, выбранный из условий сходимости. Например, если в результате двух шагов U(a,Z(W(a))) возрастает, тогда g(S)=dg(S-1), где d – параметр акселерации; d>1, r(S+1) – случайный вектор, нормируемый следующим образом:
Учет ограничений a(S+1)ÎSa производится следующим образом:
Ускорение сходимости описанного алгоритма возможно за счет более полного учета информации о направлении поиска в пространстве решений, получаемой от ЛПР. Общая схема предложенного алгоритма представлена на рисунке 2. Суть алгоритма состоит в итеративном повторении следующих шагов: - выполнение процедуры ассортиментной параметризации; - - выявление предпочтений ЛПР и корректировка значений aj, j= Первоначальные значения весов для ускорения сходимости назначаются для контрольных точек, выбранных ЛПР по формуле: wi=
На каждом шаге поиска оптимум функции предпочтения осуществлялся методом скользящего допуска {2], показатели качества модели рассчитываются после определения параметров методом наименьших квадратов. Если за заданное число итераций не будет получена ситуация безразличия по сравниваемым показателям, то принимается решение либо изменить структуру модели, либо изменить величину объема выборки данных. Качественные показатели прогностических свойств модели нумеризуются с помощью полосы прокрутки, отградуированной от 0 до 1 с шагом 0,01. На экране эксперт видит не цифры, а качественное описание показателя. Описанная методика реализована на базе приложения Excel средствами VBA и была применена для прогноза рядов динамики функционирования рынка услуг г. Твери. Качество модели оценивалось по четырем показателям: среднеквадратическое отклонение (СКО) выбранных точек, квадрат разности экспериментальных данных и теоретических с весами, визуальное сходство, СКО всех точек выборки, критерий Фишера. Значение критерия Фишера использовалось как ограничение при расчете оптимальных значений Wi. Количество контрольных точек было выбрано равным 4. В начальный момент значения для двух наборов коэффициентов α выбраны случайным образом. Начальные значения для весовых коэффициентов Wi определялись по описанным выше формулам. Допустимое число итераций принималось равным 10, в качестве первого приближения использовалась полиномиальная модель второго порядка. Формирование таблицы предпочтений ЛПР на каждой итерации осуществляется попарным сравнением критериев оценки качества модели для двух рассчитанных вариантов с помощью специально разработанной экранной формы. В ходе выполнения алгоритма были определены точки, веса Wi которых стремятся к нулю. Эти данные, слабо влияющие на современную тен- В конце работы алгоритма получаем оптимальную модель: φ(t)= -0,00011t3+0,005543t2-0,07769t+19,51824. Реальные данные по прогнозируемому периоду представлены в таблице 1. Прогнозируемые значения и отклонения от реальных представлены в таблице 2 и на рисунке 3, где точки январь 2000, февраль 2000 и март 2000 использованы как контрольные для оценки качества модели. Как видно, интерактивная модель дала более точный прогноз. Это произошло вследствие учета ситуации на рынке с помощью знаний и опыта эксперта. Кроме того, модель, построенная с помощью МНК, показала снижение объемов оказания платных услуг, хотя четко прослеживается тенденция на их увеличение. Список литературы 1. Гермейер Ю.Б. Игры с непротивоположными интересами. - М.: Изд-во МГУ,1972. 2. Химмельблау Д.. Прикладное нелинейное программирование. - М.: Мир, 1975. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=897&page=article |
Версия для печати Выпуск в формате PDF (1.53Мб) |
| Статья опубликована в выпуске журнала № 3 за 2000 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Эвристические и точные методы программной конвейеризации циклов
- Компьютер - хранитель домашнего очага
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
- Формулировка задачи планирования линейных и циклических участков кода
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
Назад, к списку статей



 }, которое состоит из двух подмножеств: X={XU}È{XT}, где {XU} – подмножество управляющих входных факторов; {XT} – подмножество контролируемых и неконтролируемых воздействий внешней среды. Часть этих факторов имеет монотонный характер изменения и вызывает такое же монотонное изменение анализируемого показателя. Существует значительная часть входных факторов изменяющихся скачкообразно, что вызывает резкое изменение производной Y (например, получение разового льготного кредитования, введение повышенных импортных пошлин, резкая девальвация рубля и т.п.).
}, которое состоит из двух подмножеств: X={XU}È{XT}, где {XU} – подмножество управляющих входных факторов; {XT} – подмножество контролируемых и неконтролируемых воздействий внешней среды. Часть этих факторов имеет монотонный характер изменения и вызывает такое же монотонное изменение анализируемого показателя. Существует значительная часть входных факторов изменяющихся скачкообразно, что вызывает резкое изменение производной Y (например, получение разового льготного кредитования, введение повышенных импортных пошлин, резкая девальвация рубля и т.п.).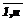 }, где n – находящийся в распоряжении объем выборки. Но для построения оптимальной модели тренда экономического показателя как динамической системы SP необходимо иметь фиксированные значения Y=Y(t), где tÎ[tn-m,tn], m>0 и m£n заранее неизвестны и характеризуют память динамической системы. Очевидно, что y(tn) – это последнее значение временного ряда. Если m>n, то данных недостаточно для построения модели тренда. Наиболее це- лесообразно величину m определять итеративным путем.
}, где n – находящийся в распоряжении объем выборки. Но для построения оптимальной модели тренда экономического показателя как динамической системы SP необходимо иметь фиксированные значения Y=Y(t), где tÎ[tn-m,tn], m>0 и m£n заранее неизвестны и характеризуют память динамической системы. Очевидно, что y(tn) – это последнее значение временного ряда. Если m>n, то данных недостаточно для построения модели тренда. Наиболее це- лесообразно величину m определять итеративным путем. Согласно приведенной схеме параметры модели тенденции будут определяться условием минимизации следующего функционала:
Согласно приведенной схеме параметры модели тенденции будут определяться условием минимизации следующего функционала: (yi– j(ti))2®min, wiÎWw ,
(yi– j(ti))2®min, wiÎWw , }, Ww – множество значений для весовых коэффициентов, например, wi ³ 0,
}, Ww – множество значений для весовых коэффициентов, например, wi ³ 0,  =1.
=1. ; вид модели y = φ(t); объем выборки, принимаемый во внимание при определении параметров модели тренда.
; вид модели y = φ(t); объем выборки, принимаемый во внимание при определении параметров модели тренда. }. Тогда очевидно, что Z={zj, j=
}. Тогда очевидно, что Z={zj, j= } будет зависеть от вектора весовых коэффициентов W={wi,i=
} будет зависеть от вектора весовых коэффициентов W={wi,i= Z(W(2))ÛU(Z(W(1)))>U(Z(W(2))),
Z(W(2))ÛU(Z(W(1)))>U(Z(W(2))),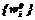 , максимизирующих функцию U(Z(W)), таких, что:
, максимизирующих функцию U(Z(W)), таких, что:  ÎWW и W0=arg max U(z1(W),…, zj(W),…, zk(W)).
ÎWW и W0=arg max U(z1(W),…, zj(W),…, zk(W)). =1}. При этом выполняются условия:
=1}. При этом выполняются условия:
 такой, что:
такой, что:
 ,
, где Ci(S+1) – случайный вектор, распределенный на единичной сфере
где Ci(S+1) – случайный вектор, распределенный на единичной сфере
 (S+1)+
(S+1)+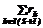 (S+1)=1–
(S+1)=1– (S+1).
(S+1). расчет оптимальных значений весовых коэффициентов wi;
расчет оптимальных значений весовых коэффициентов wi; , где m – объем выборки; с – число контрольных точек. Для остальных точек выборки весовые коэффициенты принимаются равными wi=
, где m – объем выборки; с – число контрольных точек. Для остальных точек выборки весовые коэффициенты принимаются равными wi= , i=
, i= .
. Из условия нормализации
Из условия нормализации  +(1–
+(1– ), если последняя точка не является контрольной, то wm=
), если последняя точка не является контрольной, то wm=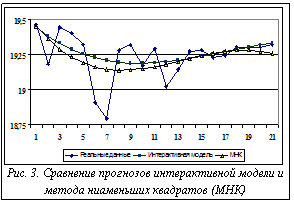 денцию развития рынка из-за событий августа 1998 года, были отброшены. Для оставшихся данных была выполнена операция дезагрегирования и выполнен переход к помесячным данным.
денцию развития рынка из-за событий августа 1998 года, были отброшены. Для оставшихся данных была выполнена операция дезагрегирования и выполнен переход к помесячным данным.