Пусть S = {S1, S2, ..., SN} – геометрические модели исходных заготовок; k1, ..., kN – количества соответствующих заготовок; S1i, S2i, …, S lii, – внутренние контуры i-й заготовки ( ). Для математического описания заготовок используется класс точечных множеств, называемых j-объектами. Обозначим Fi(x, y, Ui) = 0 – канонические уравнения общего положения j-объекта, соответствующего i-й заготовке; Ui= (ui,vi,
). Для математического описания заготовок используется класс точечных множеств, называемых j-объектами. Обозначим Fi(x, y, Ui) = 0 – канонические уравнения общего положения j-объекта, соответствующего i-й заготовке; Ui= (ui,vi, i) – параметры размещения (ui,vi – линейные,
i) – параметры размещения (ui,vi – линейные,  i – угловой). Задача проектирования карт раскроя заключается в плотном размещении заготовок в заданных областях.
i – угловой). Задача проектирования карт раскроя заключается в плотном размещении заготовок в заданных областях.
Пусть S0 = {S10, S20, …, S n0} – исходные области размещения. Требуется осуществить разбиение множества S на подмножества 
 , удовлетворяющие условиям:
, удовлетворяющие условиям:

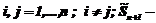 множество неразмещенных объектов. Определить для каждого объекта множества S такие значения параметров размещения
множество неразмещенных объектов. Определить для каждого объекта множества S такие значения параметров размещения 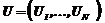 на области допустимых значений, определяемых геометрическими и технологическими ограничениями, чтобы некоторый функционал W(U) достигал экстремума. Геометрические ограничения определяются областью размещения, условиями принадлежности объектов области размещения, условиями взаимного непересечения объектов, а также способами размещения. Технологические ограничения определяются особенностями раскройного оборудования, комплектностью заготовок и др. Качество размещения определяется коэффициентом заполнения листа, объемом деловых остатков. Целевой функционал задачи размещения можно записать в следующем виде:
на области допустимых значений, определяемых геометрическими и технологическими ограничениями, чтобы некоторый функционал W(U) достигал экстремума. Геометрические ограничения определяются областью размещения, условиями принадлежности объектов области размещения, условиями взаимного непересечения объектов, а также способами размещения. Технологические ограничения определяются особенностями раскройного оборудования, комплектностью заготовок и др. Качество размещения определяется коэффициентом заполнения листа, объемом деловых остатков. Целевой функционал задачи размещения можно записать в следующем виде:
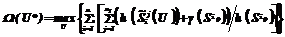 , где
, где 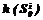 – площадь области
– площадь области  ;
;  –площадь заготовки
–площадь заготовки  , входящей в карту раскроя
, входящей в карту раскроя  ; ni – количество заготовок, входящих в
; ni – количество заготовок, входящих в  ;
;  – площадь деловых остатков.
– площадь деловых остатков.
Принцип, который положен в основу решения сформулированной задачи, состоит в декомпозиции исходной задачи на следующие взаимодействующие между собой задачи: разбиение текущего множества геометрических объектов на подмножества, соответствующие несвязным областям размещения с учетом их текущего состояния (заполнения j-объектами) по принципу в наилучший подходящий; генерация комбинаторных конфигураций из групп j-объектов; решение ло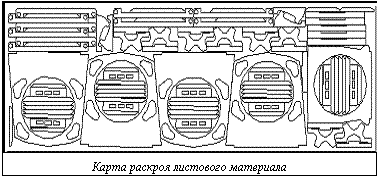 кальных задач плотного размещения j-объектов; последовательный анализ и отсев вариантов на основе p-кратного группирования объектов и прогноза значения целевой функции. На каждом этапе из множества S выбирается p объектов и решается задача такого их взаимного расположения, чтобы обеспечить выполнение заданного локального критерия оптимальности. Полученная группа добавляется в качестве нового объекта. Оценка создаваемых групп осуществляется по следующим критериям: коэффициент заполнения минимальной ортогональной оболочки; коэффициент заполнения выпуклой оболочки; коэффициент заполнения регуляризованной монотонной оболочки.
кальных задач плотного размещения j-объектов; последовательный анализ и отсев вариантов на основе p-кратного группирования объектов и прогноза значения целевой функции. На каждом этапе из множества S выбирается p объектов и решается задача такого их взаимного расположения, чтобы обеспечить выполнение заданного локального критерия оптимальности. Полученная группа добавляется в качестве нового объекта. Оценка создаваемых групп осуществляется по следующим критериям: коэффициент заполнения минимальной ортогональной оболочки; коэффициент заполнения выпуклой оболочки; коэффициент заполнения регуляризованной монотонной оболочки.
Для обеспечения геометрических ограничений предлагается специальная целочисленная дискретная аппроксимация контуров объектов. В этом методе сделан переход от стандартного способа хранения j-объектов к независимому хранению четырех границ специального вида аппроксимации  , где i=1,2,3,4 – номер границы; j=1,2,...,ki – количество узлов аппроксимации на i-й границе. Вычисление расстояния между двумя границами j-объектов при заданных значениях параметров размещения сводится к k-кратному сложению целых чисел, благодаря чему процедура вычисления расстояния более эффективна, чем вычисление расстояния в евклидовом пространстве.
, где i=1,2,3,4 – номер границы; j=1,2,...,ki – количество узлов аппроксимации на i-й границе. Вычисление расстояния между двумя границами j-объектов при заданных значениях параметров размещения сводится к k-кратному сложению целых чисел, благодаря чему процедура вычисления расстояния более эффективна, чем вычисление расстояния в евклидовом пространстве.
Общая схема размещения с учетом введенной конкретизации стратегии поиска решения будет выглядеть следующим образом:
 ,
,
где 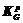 – оператор комбинаторного p-кратного группирования; f – локальный критерий качества группирования; W – глобальный критерий размещения. Область альтернативных вариантов определяется множеством комбинаторных конфигураций объектов (возможных вариантов группирования) и областью возможных значений параметров размещения U.
– оператор комбинаторного p-кратного группирования; f – локальный критерий качества группирования; W – глобальный критерий размещения. Область альтернативных вариантов определяется множеством комбинаторных конфигураций объектов (возможных вариантов группирования) и областью возможных значений параметров размещения U.
Обозначим 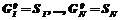 – группы нулевого уровня;
– группы нулевого уровня; 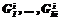 – группы i-го уровня.
– группы i-го уровня.
Множество групп i-го уровня обозначим  и будем называть частичным решением. Окончательные карты раскроя заданных областей представляют собой полное решение. Процесс решения представляется в виде многоступенчатой структуры. Каждая ступень связана с реализацией набора правил m конструирования частичных решений, подлежащих развитию на каждом шаге, реализации набора тестов Y={yi}, осуществляющих проверку тех или иных свойств у подмножеств вариантов с целью отсева частичных решений, которые не могут быть достроены до оптимальных. В набор Y входят как минимум тесты y0 – анализа допустимости решений, y1 – сравнения решений по прогнозируемым значениям целевой функции. Тогда запись Y(H i) будет обозначать множество частичных решений, исключаемых набором тестов Y.
и будем называть частичным решением. Окончательные карты раскроя заданных областей представляют собой полное решение. Процесс решения представляется в виде многоступенчатой структуры. Каждая ступень связана с реализацией набора правил m конструирования частичных решений, подлежащих развитию на каждом шаге, реализации набора тестов Y={yi}, осуществляющих проверку тех или иных свойств у подмножеств вариантов с целью отсева частичных решений, которые не могут быть достроены до оптимальных. В набор Y входят как минимум тесты y0 – анализа допустимости решений, y1 – сравнения решений по прогнозируемым значениям целевой функции. Тогда запись Y(H i) будет обозначать множество частичных решений, исключаемых набором тестов Y.
Пусть в результате k шагов получено множество частичных решений 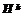 , каждое из них может быть достроено до оптимального и представлено в виде
, каждое из них может быть достроено до оптимального и представлено в виде 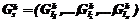 , где
, где  есть элемент из S или одна из групп вышележащих уровней. В множестве
есть элемент из S или одна из групп вышележащих уровней. В множестве 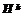 с помощью правил m выберем некоторое подмножество
с помощью правил m выберем некоторое подмножество 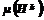 частичных решений, наиболее перспективных для дальнейшего развития. Каждое из частичных решений
частичных решений, наиболее перспективных для дальнейшего развития. Каждое из частичных решений 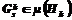 заменяется системой частичных решений вида:
заменяется системой частичных решений вида:  .
.
В результате получаем множество 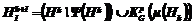 . Применим к нему набор тестов Y, получим множество
. Применим к нему набор тестов Y, получим множество 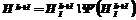 , подлежащее анализу на k+1 шаге.
, подлежащее анализу на k+1 шаге.
Прогноз и оценка качества частичных решений осуществляется с помощью решения релаксированной задачи, в которой осуществляется габаритное размещение групп или последовательно одиночное размещение групп на основе системы эвристических правил.
 ). Для математического описания заготовок используется класс точечных множеств, называемых j-объектами. Обозначим Fi(x, y, Ui) = 0 – канонические уравнения общего положения j-объекта, соответствующего i-й заготовке; Ui= (ui,vi,
). Для математического описания заготовок используется класс точечных множеств, называемых j-объектами. Обозначим Fi(x, y, Ui) = 0 – канонические уравнения общего положения j-объекта, соответствующего i-й заготовке; Ui= (ui,vi, i) – параметры размещения (ui,vi – линейные,
i) – параметры размещения (ui,vi – линейные, 
 , удовлетворяющие условиям:
, удовлетворяющие условиям:
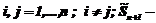 множество неразмещенных объектов. Определить для каждого объекта множества S такие значения параметров размещения
множество неразмещенных объектов. Определить для каждого объекта множества S такие значения параметров размещения 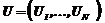 на области допустимых значений, определяемых геометрическими и технологическими ограничениями, чтобы некоторый функционал W(U) достигал экстремума. Геометрические ограничения определяются областью размещения, условиями принадлежности объектов области размещения, условиями взаимного непересечения объектов, а также способами размещения. Технологические ограничения определяются особенностями раскройного оборудования, комплектностью заготовок и др. Качество размещения определяется коэффициентом заполнения листа, объемом деловых остатков. Целевой функционал задачи размещения можно записать в следующем виде:
на области допустимых значений, определяемых геометрическими и технологическими ограничениями, чтобы некоторый функционал W(U) достигал экстремума. Геометрические ограничения определяются областью размещения, условиями принадлежности объектов области размещения, условиями взаимного непересечения объектов, а также способами размещения. Технологические ограничения определяются особенностями раскройного оборудования, комплектностью заготовок и др. Качество размещения определяется коэффициентом заполнения листа, объемом деловых остатков. Целевой функционал задачи размещения можно записать в следующем виде: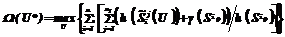 , где
, где 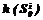 – площадь области
– площадь области 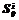 ;
;  –площадь заготовки
–площадь заготовки  , входящей в карту раскроя
, входящей в карту раскроя  ; ni – количество заготовок, входящих в
; ni – количество заготовок, входящих в  – площадь деловых остатков.
– площадь деловых остатков. кальных задач плотного размещения j-объектов; последовательный анализ и отсев вариантов на основе p-кратного группирования объектов и прогноза значения целевой функции. На каждом этапе из множества S выбирается p объектов и решается задача такого их взаимного расположения, чтобы обеспечить выполнение заданного локального критерия оптимальности. Полученная группа добавляется в качестве нового объекта. Оценка создаваемых групп осуществляется по следующим критериям: коэффициент заполнения минимальной ортогональной оболочки; коэффициент заполнения выпуклой оболочки; коэффициент заполнения регуляризованной монотонной оболочки.
кальных задач плотного размещения j-объектов; последовательный анализ и отсев вариантов на основе p-кратного группирования объектов и прогноза значения целевой функции. На каждом этапе из множества S выбирается p объектов и решается задача такого их взаимного расположения, чтобы обеспечить выполнение заданного локального критерия оптимальности. Полученная группа добавляется в качестве нового объекта. Оценка создаваемых групп осуществляется по следующим критериям: коэффициент заполнения минимальной ортогональной оболочки; коэффициент заполнения выпуклой оболочки; коэффициент заполнения регуляризованной монотонной оболочки. , где i=1,2,3,4 – номер границы; j=1,2,...,ki – количество узлов аппроксимации на i-й границе. Вычисление расстояния между двумя границами j-объектов при заданных значениях параметров размещения сводится к k-кратному сложению целых чисел, благодаря чему процедура вычисления расстояния более эффективна, чем вычисление расстояния в евклидовом пространстве.
, где i=1,2,3,4 – номер границы; j=1,2,...,ki – количество узлов аппроксимации на i-й границе. Вычисление расстояния между двумя границами j-объектов при заданных значениях параметров размещения сводится к k-кратному сложению целых чисел, благодаря чему процедура вычисления расстояния более эффективна, чем вычисление расстояния в евклидовом пространстве. ,
,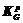 – оператор комбинаторного p-кратного группирования; f – локальный критерий качества группирования; W – глобальный критерий размещения. Область альтернативных вариантов определяется множеством комбинаторных конфигураций объектов (возможных вариантов группирования) и областью возможных значений параметров размещения U.
– оператор комбинаторного p-кратного группирования; f – локальный критерий качества группирования; W – глобальный критерий размещения. Область альтернативных вариантов определяется множеством комбинаторных конфигураций объектов (возможных вариантов группирования) и областью возможных значений параметров размещения U.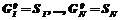 – группы нулевого уровня;
– группы нулевого уровня; 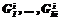 – группы i-го уровня.
– группы i-го уровня. и будем называть частичным решением. Окончательные карты раскроя заданных областей представляют собой полное решение. Процесс решения представляется в виде многоступенчатой структуры. Каждая ступень связана с реализацией набора правил m конструирования частичных решений, подлежащих развитию на каждом шаге, реализации набора тестов Y={yi}, осуществляющих проверку тех или иных свойств у подмножеств вариантов с целью отсева частичных решений, которые не могут быть достроены до оптимальных. В набор Y входят как минимум тесты y0 – анализа допустимости решений, y1 – сравнения решений по прогнозируемым значениям целевой функции. Тогда запись Y(H i) будет обозначать множество частичных решений, исключаемых набором тестов Y.
и будем называть частичным решением. Окончательные карты раскроя заданных областей представляют собой полное решение. Процесс решения представляется в виде многоступенчатой структуры. Каждая ступень связана с реализацией набора правил m конструирования частичных решений, подлежащих развитию на каждом шаге, реализации набора тестов Y={yi}, осуществляющих проверку тех или иных свойств у подмножеств вариантов с целью отсева частичных решений, которые не могут быть достроены до оптимальных. В набор Y входят как минимум тесты y0 – анализа допустимости решений, y1 – сравнения решений по прогнозируемым значениям целевой функции. Тогда запись Y(H i) будет обозначать множество частичных решений, исключаемых набором тестов Y.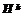 , каждое из них может быть достроено до оптимального и представлено в виде
, каждое из них может быть достроено до оптимального и представлено в виде 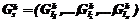 , где
, где  есть элемент из S или одна из групп вышележащих уровней. В множестве
есть элемент из S или одна из групп вышележащих уровней. В множестве 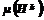 частичных решений, наиболее перспективных для дальнейшего развития. Каждое из частичных решений
частичных решений, наиболее перспективных для дальнейшего развития. Каждое из частичных решений 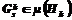 заменяется системой частичных решений вида:
заменяется системой частичных решений вида:  .
.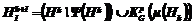 . Применим к нему набор тестов Y, получим множество
. Применим к нему набор тестов Y, получим множество 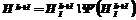 , подлежащее анализу на k+1 шаге.
, подлежащее анализу на k+1 шаге.