Эффективное конфигурирование приложений во встроенных системах реального времени
| Домарацкий Я.А. () - , Альховик А.А. () - , Перевозчиков М.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Технология построения встроенных программных систем предполагает наличие инструментальной и целевой машин. Инструментальная машина обеспечивает разработку программной системы, а целевая – ее исполнение [1]. При построении сложных встроенных программных систем общепринятым является подход, при котором разрабатываемая система состоит из двух основных частей: операционной системы (ОС) – системная часть, и приложения пользователя – прикладная часть. Важной частью технологии разработки в этом случае является фаза конфигурирования прикладной части системы для обеспечения ее функционирования под управле- нием ОС. При этом встает задача эффективного с точки зрения аппаратных затрат и накладных расходов времени выполнения конфигурирования. Для встроенных программных систем реального времени, построенных в соответствии с синхронным (time-triggered) подходом, важнейшей системной структурой данных является график активации за- дач [2], поэтому построение эффективного графика является главной составляющей решения упомянутой задачи. Структура прикладной части. Статический график строится на основе представленного разработчиком описания приложения. Основными объектами, которыми оперирует разработчик при построении приложения, являются задачи. В синхронных системах существуют задачи двух типов – периодические и спорадические. Периодические задачи реализуют действия, период которых заранее известен и строго определен. Спорадические задачи предназначены для реализации действий, период которых не определен (например, для обработки внешних и/или внутренних прерываний). Для спорадической задачи известен лишь минимальный интервал времени, который может пройти между двумя ее соседними активациями. Кроме периода периодической задачи и интервала спорадической, для построения эффективного графика необходима дополнительная информация. Ниже для каждого типа задач приведен полный список используемых в дальнейшем параметров. Если какому-либо из них может быть назначено разумное значение по умолчанию, оно приведено в скобках. Параметры периодической задачи: tp – номинальный период выполнения задачи; D – допуск на действительное значение периода задачи (= 0%); td – крайний срок выполнения задачи (= действительное значение периода); to – смещение активации задачи (= 0); tw – наихудшее время выполнения задачи; tb – наилучшее время выполнения задачи (= 0). Параметры спорадической задачи: ip – минимальный интервал времени между двумя соседними активациями задачи; iw – наихудшее время выполнения задачи. При построении статического графика основой являются периодические задачи. Информация о спорадических задачах не указывается в нем в непосредственном виде. Чтобы учесть влияние спорадических задач на работу приложения, наихудшее время выполнения каждой периодической задачи увеличивается исходя из максимальной частоты появления спорадических задач. Если в системе только одна спорадическая задача, скорректированное значение наихудшего времени выполнения периодической задачи может быть найдено как величина, к которой сходится следующее рекуррентное уравнение: tw,0=tw ; Если в системе несколько спорадических задач, то уравнение (1) усложняется следующим образом (когда спорадические задачи являются невытесняемыми):
где N – число спорадических задач в системе. Поскольку для построения графика основой являются периодические задачи, то существует общий период выполнения приложения (TП), который в простейшем случае равен наименьшему общему кратному (НОК) периодов всех задач. Размер статического графика пропорционален величине TП, и для произвольного набора задач (их периодов) он может превысить физические ресурсы аппаратных средств. Уменьшить размер статического графика можно за счет использования информации о значении допусков (D) на периоды активации задач. Введение даже небольших допусков (около 5%) часто позволяет на порядок уменьшить величину TП. Ниже описана общая схема отыскания оптимального значения TП (подробнее см. в [3]). Каждой периодической задаче приложения соответствует некоторое множество допустимых для нее значений TП. Найти оптимальное значение TП можно, отыскав пересечение этих множеств для всех периодических задач и взяв минимальное число из результирующего множества. На рисунке 1 это проиллюстрировано для приложения из трех задач со следующими значениями периодов и допусков: p1=7±1; p2=5±1; p3=9±1.5. Как видно из рисунка, для данного примера величина TП почти в 40 раз меньше величины НОК.
Для приведенного примера во время работы системы происходит всего 10 переключений контекста вместо 26, если бы это происходило для каждой задачи в отдельности. Время же переключения между задачами внутри цепочки обычно в несколько раз меньше времени переключения контекстов, а при помощи автоматической кодогенерации может быть сведено практически к нулю. Модель диспетчера ОС. Для построения алгоритма статического планирования необходимо учитывать накладные расходы ОС на обработку графика. Ниже приведена модель диспетчера синхронной ОС реального времени, используемая в дальнейшем при описании алгоритма статического планирования. Данная модель предполагает, что основным событием в системе, инициирующим работу всего приложения, является событие от системного таймера. Причем считается, что эти события возникают только в моменты времени, указываемые в статическом графике. Единицей диспетчирования в системе является цепочка задач (chain). График представляет собой таблицу, каждая ячейка которой содержит системное время (в относительных или абсолютных единицах) и идентификатор активируемой в данный момент цепочки задач. Все накладные расходы диспетчера можно разбить на следующие три группы. 1. 2. Расходы, связанные с обработкой конкретной задачи. Перед запуском каждой задачи диспетчер выполняет действия, связанные с выделением данной задаче контрольного блока, очисткой стека и инициализацией связанных с ней системных переменных (например, времени активации). Время, необходимое на выполнение данной работы, обозначим как TaskPrologue. При окончании выполнения задачи диспетчер должен возвратить в систему освободившийся контрольный блок. Время, необходимое на выполнение этой работы, обозначим как TaskEpilogue. 3. Расходы, связанные с переходом от одной задачи к другой внутри цепочки задач. Время, необходимое диспетчеру на переключение между двумя задачами внутри цепочки, обозначим как ChainGap (например, это может быть время, необходимое на увеличение индекса/указателя текущей задачи, если цепочка реализована в виде массива идентификаторов). На рисунке 3 проиллюстрированы все накладные расходы диспетчера для цепочки из трех задач (Task1-Task2-Task3). Кроме накладных расходов, статическому планировщику еще необходима информация о максимально возможном расстоянии (разнице времен) между двумя соседними точками в графике. Данная величина определяется, как правило, разрядностью системного таймера. Обозначим ее как Maximum- ScheduleGap. Алгоритм статического планирования. Как известно, для динамического планирования существует, по крайней мере, два оптимальных алгоритма диспетчирования – EDF (Earliest Deadline First) и LLF (Least Latency First). Алгоритм EDF представляется более привлекательным, поскольку при его использовании происходит меньшее число переключений контекста [4]. Поэтому описанный ниже алгоритм статического планирования основывается именно на нем, то есть статический график строится так, что при его обработке задачи исполняются точно в таком порядке, в каком они исполнялись бы, если бы работал EDF-диспетчер. В алгоритме используются следующие структуры данных. Структура Job описывает временные параметры отдельного экземпляра каждой задачи и имеет поля: arrtime – самое раннее возможное время активации (arrival time); deadline – крайний срок; bcet – время выполнения в наилучшем случае (best case execution time); wcet – время выполнения в наихудшем случае (worst case execution time); bcat – время старта в наилучшем случае (best case activation time); wcat – время старта в наихудшем случае (worst case activation time); bctt – время окончания работы в наилучшем случае (best case termination time); wctt – время окончания работы в наихудшем случае (worst case termination time). Первые четыре поля (arrtime, deadline, bcet, wcet) устанавливаются на этапе инициализации и вычисляются на основе описания задачи. Значения последних четырех полей являются результатом работы алгоритма статического планирования и при успешном результате удовлетворяют условиям (2):
Структура Chain описывает конкретную точку в графике и содержит следующие поля: arrtime – время активации цепочки задач (абсолютное); bctt – время окончания работы цепочки задач в наилучшем случае; wctt – время окончания работы цепочки задач в наихудшем случае; jobs – список задач, входящих в цепочку (список структур типа Job). В соответствии с величиной ТП строится список активации всех экземпляров всех периодических задач приложения Jobs (список структур типа Job), который является входной информацией для алгоритма статического планирования. Выходной структурой алгоритма является список Schedule (список структур типа Chain). После работы алгоритма входной список Jobs становится пустым. Перед стартом алгоритма производится инициализация всех элементов списка Jobs согласно (3) (здесь i – номер экземпляра/активации конкретной задачи):
При работе алгоритма список Jobs поддерживается в упорядоченном состоянии. Сортировка производится по следующему критерию (в порядке возрастания). Считается, что задача job1 меньше задачи job2: 1. если job1.arrtime < job2.arrtime; 2. или если job1.arrtime = job2.arrtime[1][1], то если job1.deadline £ job2.deadline. Сам алгоритм статического планирования представляет собой цикл, который оканчивается при полной очистке входного буфера Jobs. Каждая итерация цикла состоит из двух шагов. На первом шаге из списка Jobs берется первая задача в соответствии со значением самого раннего следующего события в графике. Для данной задачи делается попытка поместить ее в какую-нибудь из существующих цепочек. Если данная попытка завершается удачей, то второй шаг не выполняется и происходит переход к обработке следующей задачи из списка Jobs.
Для реализации данного алгоритма необходимо описать два критерия: критерий I, определяющий возможность добавления обрабатываемой задачи в конец некоторой цепочки, и критерий II для определения времени активации задачи (как начала новой цепочки), если ни в какую из существующих цепочек ее добавить нельзя. Критерий I. Поскольку список Jobs постоянно поддерживается в упорядоченном описанным выше способом состоянии, то каждая задача, находящаяся в начале этого списка, может быть добавлена только в конец какой-либо существующей цепочки задач. Критерием того, что обрабатываемую задачу можно добавить в конец некоторой цепочки, является выполнение следующих трех условий. 1. Последняя задача цепочки заканчивается не раньше чем может быть активирована обрабатываемая задача, то есть: 2. Если цепочка не пуста, то крайний срок последней задачи в ней должен быть не больше чем крайний срок обрабатываемой задачи, то есть:
3. Крайние сроки всех задач, которые могут быть вытеснены или отложены данной цепочкой, должны быть больше чем крайний срок обрабатываемой задачи. Критерий II. Время, в которое может быть активирована данная задача (RealActivationTime), должно удовлетворять следующим двум условиям (время новой точки в графике при этом будет равно 1. RealActivationTime должно быть не меньше чем возможное время активации задачи, то есть:
2. RealActivationTime должно быть не меньше чем время окончания последней задачи в спланированной части графика, крайний срок которой меньше или равен крайнему сроку планируемой задачи (с учетом накладных расходов на ChainPologue, TaskPrologue, TaskEpilogue, ChainEpilogue). Основываясь на приведенных выше критериях, представим псевдокод алгоритма статического планирования. 1. Вставить пустую точку в график с временем активации, равным нулю. 2. Цикл до тех пор, пока список Jobs не пуст. 2.1. ActualTime = min( Schedule[last].bctt – ChainEpilogue + ChainGap + TaskPrologue, Schedu- le[last].arrtime + ChainPrologue + TaskPrologue). 2.2. Привести список Jobs в соответствие со значением ActualTime. 2.3. Найти цепочку, в конец которой можно добавить Jobs[0] (результат поместить в CurChain). 2.3.1. Если нашли, то добавить Jobs[0] в CurChain, обновить времена всех задач, которые могут быть вытеснены или отложены данной цепочкой, удалить Jobs[0] из Jobs и перейти к шагу 2. 2.3.2. Если не нашли, то вычислить действительное время активации для Jobs[0] задачи (в соответствии с критерием II) и инициализировать вычисленным значением ActualTime. 2.4. Сохранить Jobs[0] во временную переменную CurJob. 2.5. Привести список Jobs в соответствие со значением ActualTime. 2.6. Если 2.6.1. Если нашли, то добавить Jobs[0] в CurChain, обновить времена всех задач, которые могут быть вытеснены или отложены данной цепочкой, удалить Jobs[0] из Jobs и перейти к шагу 2. 2.6.2. Если не нашли, то вычислить действительное время активации для Jobs[0] задачи (в соответствии с критерием II) и инициализировать вычисленным значением ActualTime. 2.7. Если (Schedule[last].arrtime + Maximum ScheduleGap ) < (ActualTime – TaskPrologue – ChainPrologue), то вставить в график пустую точку (с временем активации, равным Schedule[last]. arrtime + MaximumScheduleGap), обновить времена всех задач, которые могут быть вытеснены или отложены, и перейти к шагу 2. 2.8. Создать новую цепочку для Jobs[0], обновить времена всех задач, которые могут быть вытеснены или отложены данной цепочкой, удалить Jobs[0] из Jobs и перейти к шагу 2. Процедура добавления экземпляра задачи в конец существующей цепочки выглядит следующим образом (job – вставляемый экземпляр задачи, chain – цепочка):
Процедура создания новой цепочки для обрабатываемого экземпляра задачи выглядит следующим образом (job – обрабатываемый экземпляр задачи, ActivationTime – время его активации, chain – новая цепочка):
В настоящей работе рассмотрены вопросы эффективного конфигурирования приложений для синхронных ОС ЖРВ. К ним относятся вопросы экономии аппаратных ресурсов и уменьшения накладных расходов ОС. В работе описан алгоритм статического планирования, основанный на модели динамического планировщика, для которого единицей диспетчирования является цепочка задач. Благодаря описанному подходу достигается существенное снижение накладных расходов ОС на обработку (интерпретацию) построенного на инструментальной машине статического графика. Список литературы 1. Никифоров В.В., Павлов В.А. Операционные системы реального времени для встроенных программных комплексов. // Программные продукты и системы. - 1999. -№4. - С. 24. 2. Никифоров В.В., Перевозчиков М.В. Ранжирование периодов задач в системах реального времени. // Там же. - С. 16. 3. Перевозчиков М.В. Оптимизация общего периода выполнения приложения во встроенных системах реального времени. // Там же. - С. 20. 4. Xu J., Parnas D.L. Priority Scheduling Versus Pre-Run-Time Scheduling, Real-Time Systems, Vol. 18, No 1, Jan 2000. |
http://swsys.ru/index.php?id=902&lang=%E2%8C%A9%3Den&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Интегрированная система «микросреда»
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Механизм контроля качества программного обеспечения оптико-электронных систем контроля
- Автоматизированная информационная система маркетолога
- Метод интегрированного описания топологических отношений в геоинформационных системах

 . (1)
. (1) ,
,![Подпись:
G = {8} È [15, 16] È [18, 21] È [22.5, ¥); ТП = 8; НОК(5, 7, 9) = 315.
Рис. 1. Схема отыскания оптимального значения ТП](uploaded/image/2000-4/image074.gif) Структура системной части. Второй составляющей задачи оптимального конфигурирования приложения является минимизация накладных расходов во время работы системы. Основным компонентом ОС реального времени, определяющим общую производительность системы, является динамический планировщик (диспетчер). Главной задачей диспетчера в синхронных системах является интерпретация построенного на инструментальной машине статического графика. Основными временными характеристиками диспетчера, влияющими на общую производительность системы, являются время сохранения контекста выполняющейся задачи при активации более приоритетной и время восстановления контекста вытесненной задачи после окончания более приоритетной. Поэтому для уменьшения накладных расходов системы на обработку статического графика необходимо уменьшить число переключений контекстов в системе. Достичь этого можно, объединяя последовательно активируемые задачи в цепочки и указывая в графике время активации для всей цепочки только один раз. Цепочка при этом представляет собой последовательность задач, выполняющихся на одном стеке и приоритете, в силу этого смена контекста будет происходить только при активации и окончании работы цепочки, а не для каждой задачи в отдельности. На рисунке 2 описанная схема проиллюстрирована для приложения из трех задач со следующими временными характеристиками: Task1(tp=5, tw=1), Task2(tp=7.5, tw=2), Task3(tp=10, tw=3).
Структура системной части. Второй составляющей задачи оптимального конфигурирования приложения является минимизация накладных расходов во время работы системы. Основным компонентом ОС реального времени, определяющим общую производительность системы, является динамический планировщик (диспетчер). Главной задачей диспетчера в синхронных системах является интерпретация построенного на инструментальной машине статического графика. Основными временными характеристиками диспетчера, влияющими на общую производительность системы, являются время сохранения контекста выполняющейся задачи при активации более приоритетной и время восстановления контекста вытесненной задачи после окончания более приоритетной. Поэтому для уменьшения накладных расходов системы на обработку статического графика необходимо уменьшить число переключений контекстов в системе. Достичь этого можно, объединяя последовательно активируемые задачи в цепочки и указывая в графике время активации для всей цепочки только один раз. Цепочка при этом представляет собой последовательность задач, выполняющихся на одном стеке и приоритете, в силу этого смена контекста будет происходить только при активации и окончании работы цепочки, а не для каждой задачи в отдельности. На рисунке 2 описанная схема проиллюстрирована для приложения из трех задач со следующими временными характеристиками: Task1(tp=5, tw=1), Task2(tp=7.5, tw=2), Task3(tp=10, tw=3).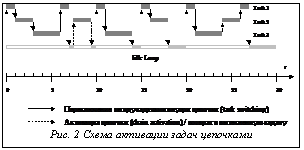 Расходы, связанные с обработкой события от системного таймера. При возникновения события от системного таймера диспетчер должен, как минимум, запрограммировать таймер на следующее событие, сохранить контекст выполнявшейся на данный момент задачи, распределить стек для активируемой цепочки задач и перейти к обработке задачи, находящейся в начале цепочки. Время, необходимое на выполнение данной работы, обозначим как ChainPrologue. После завершения работы последней задачи в активированной цепочке диспетчер должен, как минимум, вернуть распределенный стек системе, восстановить контекст вытесненной задачи и возобновить ее работу. Время, необходимое на выполнение данной работы, обозначим как ChainEpilogue. Поскольку действия, выполняемые на этапе ChainPrologue, являются критическими и должны выполняться в режиме исключения, статический график необходимо построить таким образом, чтобы время между его соседними точками было не меньше значения ChainPrologue.
Расходы, связанные с обработкой события от системного таймера. При возникновения события от системного таймера диспетчер должен, как минимум, запрограммировать таймер на следующее событие, сохранить контекст выполнявшейся на данный момент задачи, распределить стек для активируемой цепочки задач и перейти к обработке задачи, находящейся в начале цепочки. Время, необходимое на выполнение данной работы, обозначим как ChainPrologue. После завершения работы последней задачи в активированной цепочке диспетчер должен, как минимум, вернуть распределенный стек системе, восстановить контекст вытесненной задачи и возобновить ее работу. Время, необходимое на выполнение данной работы, обозначим как ChainEpilogue. Поскольку действия, выполняемые на этапе ChainPrologue, являются критическими и должны выполняться в режиме исключения, статический график необходимо построить таким образом, чтобы время между его соседними точками было не меньше значения ChainPrologue. (2)
(2) (3)
(3) В противном случае осуществляется переход ко второму шагу. На нем вначале вычисляется актуальное время активации обрабатываемой задачи исходя из ее временных параметров и параметров уже спланированной части графика. Список Jobs переупорядочивается в соответствии с полученным значением и из него опять берется первая задача. Если взятая задача отличается от той, что была взята на первом шаге, то для нее тоже делается попытка вставить ее в какую-либо из уже существующих цепочек. Если попытка заканчивается успехом, то осуществляется переход к следующей итерации цикла. В противном случае для данной задачи вычисляется актуальное время активации исходя из ее временных параметров и временных параметров уже спланированной части графика. Если разница во времени между вычис- ленным значением и последней точкой в сплани- рованной части графика с учетом накладных рас- ходов больше максимально допустимого значения (Maximum-ScheduleGap), то создается пустая точка в графике. В противном случае для данной задачи создается новая цепочка. На этом второй шаг заканчивается и происходит переход к следующей итерации цикла.
В противном случае осуществляется переход ко второму шагу. На нем вначале вычисляется актуальное время активации обрабатываемой задачи исходя из ее временных параметров и параметров уже спланированной части графика. Список Jobs переупорядочивается в соответствии с полученным значением и из него опять берется первая задача. Если взятая задача отличается от той, что была взята на первом шаге, то для нее тоже делается попытка вставить ее в какую-либо из уже существующих цепочек. Если попытка заканчивается успехом, то осуществляется переход к следующей итерации цикла. В противном случае для данной задачи вычисляется актуальное время активации исходя из ее временных параметров и временных параметров уже спланированной части графика. Если разница во времени между вычис- ленным значением и последней точкой в сплани- рованной части графика с учетом накладных рас- ходов больше максимально допустимого значения (Maximum-ScheduleGap), то создается пустая точка в графике. В противном случае для данной задачи создается новая цепочка. На этом второй шаг заканчивается и происходит переход к следующей итерации цикла.
 .
. .
. ):
): .
. , то найти цепочку, в конец которой можно добавить Jobs[0] (результат поместить в CurChain).
, то найти цепочку, в конец которой можно добавить Jobs[0] (результат поместить в CurChain).
