Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Статическая обработка спецификаций программных систем реального времени
Аннотация:
Abstract:
| Авторы: Данилов М.В. () - , Никифоров В.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15847 |
Версия для печати Выпуск в формате PDF (1.83Мб) |
Автоматическое оборудование в связных и производственных системах, на транспорте и в быту все шире оснащается компьютерными системами реального времени (СРВ). Во многих случаях требования к своевременности выполнения функций этих систем являются не менее важными, чем требования логической корректности. Технология разработки таких систем должна гарантировать не только логическую корректность результатов выполнения функций системы, но и корректность распределения моментов получения этих результатов во времени [1]. Отсюда возникает необходимость составления детальных спецификаций свойств задач, образующих программную систему, составления явных и полных спецификаций межзадачных отношений. Технология разработки должна включать комплекс таких методов и средств статической обработки этих спецификаций, которые обеспечивали бы достижение требуемого уровня предсказуемости поведения программной системы. Задачи статической обработки. В ряду задач статической обработки спецификаций СРВ выделяется подмножество, являющееся общим для программных систем произвольного назначения: - преобразование текстов языков высокого уровня в исполняемые модули (компиляция и сборка); - оптимизация кода в соответствии с выбранными критериями (по памяти, по быстродействию). Другое подмножество составляют задачи, которые всегда актуальны для СРВ, и в некоторых случаях могут оказаться актуальными для более широкого класса систем. К таким задачам относятся: а) оценка объема аппаратных ресурсов, требуемых для выполнения прикладных задач, б) проверка логической корректности системы межзадачных взаимодействий. В качестве примеров, выделяемых задачам аппаратных ресурсов, можно указать: ресурс процессорного времени, требуемый для выполнения отдельной задачи; ресурс памяти, динамически выделяемой из общесистемного пула; требуемый объем стекового пространства. Необходимая точность учета времени выполнения задач определяется жесткостью требований своевременности выполнения функций СРВ и высокой степени утилизации программной системой имеющегося ресурса процессорного времени. При разработке жестких СРВ с плотной загрузкой процессора возникает необходимость точной оценки наихудшего времени выполнения задачи (worst case execution time – WCET) и наилучшего времени (best case execution time – BCET). Необходимость тщательного учета расхода динамически выделяемой памяти в случае СРВ обусловлена недопустимостью отказа задаче в выполнении ее запроса на выделение памяти. Проверка логической корректности системы межзадачных взаимодействий актуальна для большинства многозадачных систем. В случае СРВ, в особенности СРВ жесткого типа, необходимо на этапе статической обработки убедиться в том, что в ходе работы системы обеспечивается: - целостность разделяемых структур данных; - должный порядок логически связанных действий, выполняемых различными задачами; - отсутствие тупиков; - отсутствие взаимных блокировок задач. Традиционные методы обеспечения целостности разделяемых структур данных опираются на защиту критических секций путем использования таких синхронизирующих механизмов, как семафоры и мютексы [6]. Для обеспечения нужного порядка действий, реализуемых различными задачами (например, когда одна задача обрабатывает данные, генерируемые другой задачей), используются те же семафоры, а также события, сигналы и тому подобные синхронизирующие механизмы. Однако при увеличении числа синхронизирующих связей возрастает опасность возникновения таких синхронизационных дефектов, как тупики и взаимные блокировки. Обнаружение потенциальной возможности возникновения синхронизационных дефектов на этапе статической обработки может оказаться трудной задачей. Поэтому разработчики многозадачных программных систем начинают ориентироваться на использование такого состава средств операционных систем реального времени (ОСРВ, которые упрощают проверку корректности программной системы на предмет невозможности возникновения такого рода дефек- тов. Перечисленные задачи статической обработки актуальны как для СРВ, так и для программных систем произвольного назначения. Вместе с тем можно указать такие задачи статической обработки, которые являются специфическими для СРВ. К ним можно, в частности, отнести: · статическое распределение приоритетов прикладных задач; · составление статических графиков генерации системных событий; · оценку продолжительности работы программной системы при блокированных прерываниях (возможно, с разбивкой по уровням приоритета процессора); · оценку продолжительности захвата задачей разделяемых информационных ресурсов; · анализ выполнимости задач жесткого реального времени (ЖРВ) в отведенные сроки (schedula- bility analysis). Приоритеты должны назначаться таким образом, чтобы в максимально возможной мере обеспечить своевременность выполнения задач. В СРВ, как правило, реализуется механизм вытеснения: если в числе претендентов на процессорное время появляется задача с приоритетом более высоким, чем приоритет текущей задачи, то процессор переключается на выполнение вновь появившейся задачи. Известно, что если относительные сроки выполнения задач не превосходят периодов их активизации и задачи не связаны синхронизационными отношениями (отсутствуют ограничения предшествования, разделяемых ресурсов, блокировки механизмов планирования и т.п.), то оптимально монотонное по срокам назначение приоритетов: чем короче относительный срок выполнения задачи, тем выше ее приоритет. В период исполнения для управления такими задачами достаточно иметь механизм приоритетного обслуживания с вытеснением. В случае комплекса прикладных задач, связанных синхронизационными отношениями, рациональное назначение приоритетов может оказаться нетривиальной задачей. В период исполнения могут потребоваться дополнительные механизмы управления задачами. В частности, могут потребоваться механизмы исполнения статически и динамически формируемых графиков системных событий (например, графиков генерации сигналов, порождения задач, исчерпания тайм-аутов). В период исполнения программных систем с циклическим ритмом работы могут потребоваться системные механизмы интерпретации статических графиков (циклограмм), предопределяющих временную привязку выполняемых системой действий. При составлении графиков необходимо учитывать статические оценки наихудшего времени выполнения задач (WCET). Если фрагменты кода задач выполняются при блокированных прерываниях или в составе задач имеются критические секции, то в ходе статической обработки наряду с временем выполнения всей задачи следует получить оценки худшего времени выполнения этих фрагментов. Такие данные могут потребоваться для получения гарантий своевременного выполнения прикладных задач. Механизмы периода исполнения СРВ. При статической обработке спецификаций программной системы (назначении приоритетов задач, составлении статических графиков, проверке гарантий своевременного выполнения задач) учитываются особенности реализации механизмов управления задачами в ходе их исполнения. В ОСРВ наряду с механизмами, общими для многозадачных программных систем (порождение/завершение, приостановка/возобновление, синхронизация задач и т.п.), используются специфические механизмы, ориентированные на обеспечение требований реального времени. Например: · ограничение числа итераций в операторах цикла (гарантирует исполнение оператора в рамках ограниченного временного интервала); · тайм-ауты (неординарное завершение операции или задачи по истечению выделенного для нее временного интервала); · переключение на варианты грубой обработки данных (imprecise computations) в случае возникновения дефицита процессорного времени; · синхронизирующие механизмы, предотвращающие неконтролируемую инверсию приоритетов. Как видно из примера, этот несложный прием позволяет ограничить продолжительность инверсии приоритетов. Однако использование протокола наследования приоритетов не исключает возможности выхода системы из строя по причине взаимной блокировки. В последнее десятилетие в состав механизмов для задач, разделяющих ресурсы, стали включаться такие методы защиты разделяемых ресурсов, которые исключают возможность взаимных блокировок. К этим методам относится протокол пороговых приоритетов (priority ceiling protocol – PCP), суть которого в следующем [3]. С каждым ресурсом связывается некий пара-метр – порог ресурса, равный высшему приоритету задачи, которая может захватить этот ресурс. Задаче разрешается захватить ресурс в том случае, когда ее приоритет выше, чем пороги всех ресурсов, занятых в настоящее время другими задачами. Таким образом, задача, занявшая ресурс, может блокировать выполнение более приоритетных задач. Задача, владеющая ресурсом, наследует высший из приоритетов тех задач, которые ею блокируются в текущий момент. С понятием порога ресурса связан еще один метод удовлетворения запросов на ресурсы – протокол превентивного наследования приоритета старшего претендента (highest locker – HL) на ресурс. Суть метода в том, что приоритет задачи занимающей ресурс, повышается (на весь период владения ресурсом) до уровня порога занимаемого ресурса. Таким образом, задача с относительно низким исходным приоритетом может задержать выполнение вновь порожденных задач с более высоким значением исходного приоритета. Исключительно за счет таких задержек обеспечиваются полезные свойства метода: задачи не могут перейти в состояние ожидания. Тем более, не может идти речи о взаимных блокировках. Как следствие, при использовании этого протокола уменьшается количество переключений контекста задач. Кроме того, метод позволяет задачам, разделяющим ресурсы, выполняться в одностековом режиме, что особенно важно для систем с существенными ограничениями на объем доступной оперативной памяти. Анализ выполнимости. В случае жестких СРВ ограничения на сроки выполнения части задач определены жестко в том смысле, что их нарушение может привести к катастрофическим последствиям [2] (это задачи ЖРВ). Конструирование систем ЖРВ, требует от разработчика гарантий того, что при любой нагрузке выполнение всех задач ЖРВ будет завершено в срок. Методы доказательства выполнимости ограничений ЖРВ опираются на проверку более или менее грубых достаточных условий выполнимости. Методы, опирающиеся на проверку слишком грубых условий, приводят к слишком пессимистическим оценкам выполнимости в том смысле, что их использование во многих случаях ведет к отказу от решений, которые в действительности адекватны имеющимся ограничениям. Следствие пессимизма – низкий уровень утилизации ресурсов системы и необходимость использования более мощных, а значит, и более дорогих аппаратных средств. Ниже рассматриваются известные методы доказательства выполнимости систем ЖРВ а также подходы к усовершенствованию этих методов, обеспечивающие снижение степени их пессимизма. Рассматриваемые методы ограничиваются рамками модели, в которой система ЖРВ представляет собой множество периодических задач S = {t1, t2, … , tn}. Каждая из задач ti выполняется либо строго периодически, либо эпизодически (спорадические задачи); j-е выполнение ti,j задачи ti называется экземпля- ром ti,j задачи ti. Таким образом, каждой задаче ti соответствует последовательность {t i,1, t i,2, … } ее экземпляров. В тех случаях, когда контекст изложения исключает двусмысленность, термин “задача ti” может использоваться в смысле “экземпляр ti,j зада- чи ti”. Задачи и их экземпляры характеризуются, в частности, следующими параметрами: · Ai,j – момент порождения j-го экземпляра ti,j задачи ti; · Тi – период задачи ti; для строго периодических задач величина Тi равна величине временного интервала между порождениями соседних экземпляров задачи (Тi = Ai,j - Ai,j+1); для спорадических задач Тi < Ai,j - Ai,j+1; · Сi – время выполнения задачи ti в худшем случае (WCET); · di,j – абсолютный срок выполнения экземпляра ti,j задачи ti; di,j представляет конкретную точку на временной оси, конкретный момент времени, до наступления которого необходимо завершить выполнение экземпляра ti,j задачи ti; · Di – относительный срок выполнения зада- чи ti (relative deadline); Di = di,j - Ai,j (отметим, что параметр Di имеет смысл только в случае, если величина разности di,j - Ai,j совпадает для всех экземпляров ti,j задачи ti). Отметим также, что для нормального функционирования системы необходимо выполнение следующих отношений: Ci £ Di £ Ti. В основе рассматриваемых ниже методов анализа выполнимости лежат некоторые соотношения, составляющие основу базового подхода к анализу выполнимости системы ЖРВ. Базовый подход обеспечивает анализ независимых задач и с неизменными значениями параметров. Дальнейшее совершенствование методов анализа выполнимости связано со смягчением этих ограничений. Базовый подход к анализу выполнимости систем задач ЖРВ ориентирован на проверку своевременности выполнения независимых периодических задач. Здесь под независимостью понимается отсутствие таких элементов структуры межзадачных отношений, как использование разделяемых ресурсов и взаимная синхронизация выполнения задач. Для каждой задачи ti определяется максимальное значение времени отклика Ri – реального времени выполнения задачи с учетом вытеснения более приоритетными задачами. Максимальное значение времени отклика (наименее благоприятная ситуация) возникает тогда, когда в момент порождения зада- чи ti порождаются и все более приоритетные задачи. Момент порождения задачи ti в такой наименее благоприятной ситуации называется критическим (critical instant). При порождении задачи ti в критический момент достигается максимальная задержка Ii ее выполнения по причине вытеснения более приоритетными задачами. Максимальное время отклика задачи ti складывается из наихудшего времени Ci ее выполнения ti и максимального времени Ii ее вытеснения: Ri=Ci+Ii. (1) Задача ti всегда будет завершаться своевременно, если максимальное значение времени отклика не превышает относительного срока ее выполнения (R i £ Di). Задача tj вытесняет задачу ti в том случае, если tj имеет больший приоритет, чем ti. Так как все задачи независимы, то общее время вытеснения ti равно сумме ее вытеснений высокоприоритетными задачами tj:
где hp(i) – множество более приоритетных, чем ti задач. Подставив (2) в (1), получаем:
Отметим, что время отклика Ri фигурирует как в левой, так и в правой частях уравнения (3), то есть формула рекурсивна. Найти Ri можно, итеративно выполняя вычисления по формуле:
где Ri0 = 0. С возрастанием n значения Rin не убывают. При последовательном вычислении значений Rin за конечное число шагов n достигается такое максимальное значение Rin, при котором Максимальное значение Rin+1 = Rin дает решение для Ri в выражении (3). Если для каждой из задач ti Î{t1, t2, … , tn} максимальное значение времени отклика Ri, вычисленное по формуле (3), не превосходит относительного срока выполнения этой задачи (Ri £ Di ), то система {t1, t2, … , tn } является выполнимой. Представленный базовый подход к анализу выполнимости системы задач ЖРВ опирается на предположение о независимости задач. Между тем в СРВ распространенной практикой является использование разделяемых ресурсов, кроме того, задачи часто связаны отношением предшествования. Ниже приводятся способы расширения базового подхода, обеспечивающие охват систем СРВ, содержащих взаимосвязанные задачи. Анализ выполнимости СРВ, содержащих разделяемые ресурсы. При выполнении систем задач с разделяемыми ресурсами наихудшее время отклика Ri для задачи ti увеличивается на величину фактора блокирования Bi – максимально возможного времени ее блокирования менее приоритетными задачами, захватившими разделяемый ресурс:
Как отмечалось выше, использование синхронизирующих механизмов, базирующихся на понятии порога ресурса, обеспечивает высокую степень предсказуемости поведения системы. Оказывается, что для систем с такими синхронизирующими механизмами введение дополнительного ограничения, состоящего в требовании вложенности критических секций (ресурсы освобождаются в порядке, обратном их захвату), позволяет найти аналитическое выражение для фактора блокирования Bi и тем самым расширить базовый подход к анализу выполнимости системы задач ЖРВ на случай задач, связанных с использованием разделяемых ресурсов. Исходными данными для расчета фактора блокирования Bi задачи ti являются значения длин критических секций задач, имеющих приоритеты меньшие, чем у ti; (под длиной csj,r критической секции подразумевается максимальное время блокирования ресурса r зада- чей tj ). Значение времени блокирования Bi представляется следующим выражением:
что означает: время блокирования Bi задачи ti равно наибольшей длине csk,r критической секции задачи k, блокирующей ресурс r. При поиске максимального значения csk,r учитываются все те и только те критические секции, которые удовлетворяют следующим условиям: задача k имеет приоритет меньший, чем задача i; задача k использует ресурс r; приоритетный порог ресурса r выше либо равен приоритету за- дачи i. Подставляя (5) в (4), получаем метод анализа выполнимости системы задач с разделяемыми ресурсами для случая использования синхронизирующих механизмов с приоритетными порогами при условии вложенности критических секций. Отношения предшествования. Ограничение предшествования (precedence constraints) между задачами ta и tb обозначается как ta ®tb и означает, что выполнение задачи ta должно быть завершено до начала выполнения задачи tb [4]. Практика построения СРВ показывает, что в большинстве случаев множество отношений предшествования имеет простую структуру и представимо в виде цепочек. В настоящей статье мы ограничимся рассмотрением таких систем задач с отношениями предшествования, которые отвечают следующим условиям: множество отношений предшествования ограничено простыми непересекающимися цепочками PCi = (t i, 1 ® t i, 2 ® ...® t i,k ); · для задач, входящих в цепочку предшествования, устанавливается единый относительный срок выполнения.
В этом случае для проверки выполнимости системы задач ЖРВ достаточно убедиться в гарантиях своевременного выполнения последней задачи в каждой цепочке. Простейший способ реализации задач, связанных простыми цепочками предшествования, состоит в соответствующем назначении приоритетов задач, входящих в цепочку. Первая задача в цепочке получает максимальный приоритет, приоритеты последующих задач монотонно понижаются. Таким образом, одновременно порождаемые задачи цепочки выполняются в нужном порядке. Этот способ применим в случае, если связанные отношениями предшествования экземпляры задач t a, j ® t b, j порождаются либо одновременно (A a, j = A b, j ), либо последовательно (A a, j < A b, j ). Учет накладных расходов на выполнение функций ОС. Управление задачами (порождение/завершение, удовлетворение запросов на ресурсы, прочие синхронизирующие операции) выполняется ОС. Выполнение этих операций вызывает соответствующие затраты процессорного времени – накладные расходы на работу ОС. В частности, при смене текущей задачи процессорное время тратится на переключение контекста (context switch). Учет этого времени может осуществляться путем добавления накладных расходов ОС к общему времени выполнения задачи. В соответствии с таким подходом выражение (3) для времени отклика приобретает вид:
где C’ – время, необходимое для выполнения самой задачи; Csw – время переключения контекста. В таком виде выражение для Ri включает как время вы- полнения собственно алгоритмов задачи, так и время, необходимое для двух переключений контекста: инициализирующего и завершающего задачу. При выполнении анализа по формуле (6) подразумевается, что переключение контекста – часть задачи, которая должна быть выполнена с соблюдением установленных для задачи сроков. Однако это не всегда справедливо. Внутренние сроки выполнения (internal deadlines). В [5] приводится ряд аргументов в пользу того, чтобы сроки выполнения задачи устанавливались лишь для той ее части, результаты выполнения которой наблюдаемы извне. Обращается внимание на то, что последнее наблюдаемое событие не всегда совпадает с окончанием задачи, то есть за последней выдаваемой задачей информацией может следовать ряд внутренних операций, для выполнения которых нет оснований устанавливать жесткие сроки. С затронутой точки зрения структура задачи изображается диаграммой (рис. 3). Блок а соответствует инициализирующему переключению контекста, блок b включает действия, определяемые целями выполнения задачи (вплоть до последнего наблюдаемого события), блок с отражает часть задачи, в ходе выполнения которой производятся действия, необходимые для корректного завершения задачи, блоку d соответствует переключение контекста по завершении задачи. Таким образом, жесткий срок должен устанавливаться не для момента завершения всей задачи, а для момента завершения некоего внутреннего блока задачи – блока b (внутренний срок выполнения). Соответственно изменяется выражение для времени отклика:
где CiD обозначает время выполнения жесткой части задачи, для которой установлены реальные сроки (то есть только блоки а и b); CjТ соответствует полному времени выполнения задачи. Формулы (3, 4, 6, 7) отражают вехи совершенствования техники оценки выполнимости систем задач ЖРВ. В рамках настоящей работы мы не можем отразить полный перечень известных сегодня методов усовершенствования анализа выполнимости. Эти усовершенствования обеспечивают снятие тех или иных ограничений на структуру межзадачных отношений, обеспечивают все более точную оценку загрузки процессора комплексами задач ЖРВ, все более эффективную загрузку аппаратных ресурсов при гарантии своевременного выполнения задач. Вместе с тем практика построения систем ЖРВ требует дальнейшего накопления методов анализа выполнимости, обеспечивающих более полный учет структурных особенностей комплексов задач ЖРВ. Ниже представлены некоторые результаты, полученные авторами в этом направлении. Отношения предшествования с внутренними сроками выполнения. Как отмечено выше, для реализации задач, связанных отношениями предшествования, применяется метод монотонного понижения приоритетов: первая задача в цепочке получает максимальный приоритет, приоритеты последующих задач монотонно понижаются; каждая следующая задача в цепочке получает в свое распоряжение ресурс процессора не раньше чем полностью закончат выполнение все предыдущие задачи. Если задачи в цепочке PCi = (t i, 1 ® t i, 2 ® ...® t i,k ) имеют внутренние сроки выполнения (рис. 3), то при таком подходе задача ti,j должна ожидать окончания выполнения не только жестких блоков a и b задач ti,0…ti,j-1, но и блоков c и d, которые лежат за рамками жесткой части задачи; время выполнения последовательности жестких блоков задач ti,0-ti,j, из цепочки PCi представляется выражением: CDPC j = CDj + S k< j Ckr . Уменьшение значения C DPC j может быть достигнуто, если вместо монотонного понижения приоритетов применить монотонное повышение приоритетов задач по мере продвижения от начала к концу цепочки PCi; при этом необходимо, чтобы последним наблюдаемым событием каждой задачи (завершающей операцией блока b) было явное разрешение начала выполнения следующей задачи цепочки. Тогда выражение для CDPC j приобретает вид: CDPC j = S k < j CDk. Рассмотрим на примере (рис. 4), как предлагаемое решение способствует уменьшению времени отклика для цепочки предшествования. Задачи t1, t2, t3 с внутренними сроками выполнения связаны цепочкой отношений предшествования: PC = (t1®t2®t3). Как видно из рисунка, в случае монотонного повышения приоритетов последнее наблюдаемое событие цепочки происходит значительно раньше (момент t4), чем при монотонно понижающихся приоритетах. Сокращение общего объема действий, выполнение которых должно быть завершено в срок, способствует уменьшению времени отклика цепочки, а значит, увеличивает шансы задач быть признанными выполнимыми. Наследование приоритетов и внутренние сроки выполнения. Как отмечалось выше, необходимым атрибутом СРВ являются такие механизмы предотвращения неконтролируемой инверсии приоритетов, как протокол превентивного наследования приоритетов. Для оценки выполнимости систем, использующих этот механизм, служат формулы (4) и (5). Отметим, что в этих формулах никак не отражается изменение приоритета вследствие наследования. Это объясняется тем, что задача, захватывающая ресурс, должна освободить его до завершения работы (до завершающего переключения контекста). В момент, когда приоритет задачи снижается до обычного уровня, ее выполнение сразу прерывается более приоритетными задачами, выполнение которых было блокировано. Таким образом, факт наследования приоритетов никак не отражается на выражениях для времени отклика. Ситуация изменяется при переходе к более адекватной модели внутренних сроков выполнения задач.
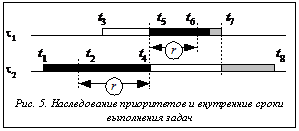
б) Рис. 4. Порядок выполнения блоков задач, связанных отношением предшествования: а) монотоннопонижающиеся приоритеты; б) монотонноповышающиеся приоритеты
Рассмотрим пример (рис. 5). Две задачи t1 и t2 разделяют ресурс r. Последним наблюдаемым событием низкоприоритетной задачи t2 является освобождение ресурса. Появление высокоприоритетной задачи t1 во время выполнения критической секции задачи t2 повлияет на время выполнения лишь завершающей (нежесткой) части низкоприоритетной задачи и, следовательно, не должно учитываться в выражении для времени отклика. В случае, когда последним наблюдаемым событием задачи является освобождение разделяемого ресурса, формула расчета времени отклика приобретает вид:
Сначала производится расчет времени отклика R’i для части задачи ti, предшествующей захвату ресурса (r), освобождение которого будет последним наблюдаемым событием. При этом учитывается вытеснение всеми задачами, обладающими приоритетом большим, чем у данной задачи. Затем вычисляется время отклика Ri всей жесткой части задачи. При этом считается, что прервать задачу ti во время выполнения жесткой секции ресурса r могут только задачи, способные преодолеть приоритетный порог, установленный при захвате ресурса. Последовательности экземпляров задач. В формулах для времени отклика, начиная с формулы (3), полагается, что наихудшее время выполнения Ci(k) серии из k подряд следующих экземпляров ti,j, ti,( j + 1), ..., ti,( j + k – 1) задачи ti кратно наихудшему времени Ci выполнения одного экземпляра этой задачи: Ci (k) = kCi . Однако в реальных системах нередко встречаются задачи с такими ветвями, которые имеют большое время выполнения, но выполняются достаточно редко и никогда не выполняются в двух подряд следующих экземплярах задачи. Следовательно, для таких задач имеет место отношение Ci (k) < kCi , что позволяет соответствующим образом усилить выражения (3, 4, 6, 7) и все им подобные. По мере развития технологии программирования расширяется состав свойств, параметров, атрибутов, отражающих особенности задач и структуры межзадачных отношений в программных комплексах, обеспечивающих функционирование СРВ. Соответственно усложняются языковые средства, используемые для спецификаций системных отношений в таких программных комплексах, расширяется состав целей и методов статической обработки спецификаций СРВ. В частности, в последнее десятилетие интенсивно развиваются методы построения жестких СРВ, эффективно использующих процессорное время. Предложенные в настоящей статье методы учета внутренних сроков выполнения задач учета времени выполнения последовательностей экземпляров задач представляют собой очередные шаги в этом направлении. Список литературы 1. Никифоров В.В., Павлов В.А. Операционные системы реального времени для встроенных программных комплексов. // Программные продукты и системы. - 1999.- №4.- С.24-30. 2. Tindell K., Hansson H. Real Time Systems by Fixed Priority Scheduling. DoCS, Uppsala University, 1997. 3. Audsley N.C. Resource Control For Hard Real-Time Systems. University of York, UK, 1991. 4. Larsson J. ScheduLite: A Fixed Priority Scheduling Analysis Tool. Uppsala University, 1996. 5. Gerber R., Hong S. Semantic-Based Compiler Transformations for Enhanced Schedulability. University of Maryland, 1993. 6. Сорокин С. Системы реального времени: операционные системы. // Современные технологии автоматизации. - 1997.- №2.- С.22-29. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=910&page=article |
Версия для печати Выпуск в формате PDF (1.83Мб) |
| Статья опубликована в выпуске журнала № 4 за 2000 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- Зарубежные базы данных по программным средствам вычислительной техники
- Эволюционная модель формирования структур виртуальных предприятий
- Формирование программ развития больших систем административно-организационного управления
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
Назад, к списку статей





 , (2)
, (2) . (3)
. (3) ,
, .
. . (4)
. (4) , (5)
, (5)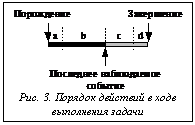 Требование непересечения цепочек означает, что ta и tb включены соответственно в две различные цепочки taÎPCi и tbÎPCj, (PCi ¹PCj ), что это две различные задачи (ta¹tb ). Второе требование означает, что если taÎPCi и tbÎPCi, то для всех j выполняется равенство da, j = db, j.
Требование непересечения цепочек означает, что ta и tb включены соответственно в две различные цепочки taÎPCi и tbÎPCj, (PCi ¹PCj ), что это две различные задачи (ta¹tb ). Второе требование означает, что если taÎPCi и tbÎPCi, то для всех j выполняется равенство da, j = db, j. , (6)
, (6) , (7)
, (7)

 В ряде случаев логическим завершением задачи является запись результатов выполнения в разделяемую область памяти. Тогда последним наблюдаемым событием задачи будет освобождение разделяемого ресурса. В таком случае на время отклика не будут влиять более приоритетные задачи, появившиеся во время работы с разделяемым ресурсом и заблокированные вследствие наследования приоритетов.
В ряде случаев логическим завершением задачи является запись результатов выполнения в разделяемую область памяти. Тогда последним наблюдаемым событием задачи будет освобождение разделяемого ресурса. В таком случае на время отклика не будут влиять более приоритетные задачи, появившиеся во время работы с разделяемым ресурсом и заблокированные вследствие наследования приоритетов. ,
, .
.