Математическое моделирование социально-экономических процессов с целью получения прогнозной информации является одним из важнейших направлений современной социологии. Большинство существующих подходов к данному вопросу в основном связаны со стремлением определить некую аналитическую зависимость между элементами исследуемого процесса и описать процесс в виде некоторого математического уравнения или системы уравнений, связывающих основные его показате- ли [1]. В этой связи следует заметить, что сложность социально-экономических процессов часто не позволяет в рамках данного подхода получить модели, адекватно описывающие полученные статистические данные.

Другим основным интенсивно развивающимся направлением является использование для исследования и моделирования социально-экономических процессов нейросетевого подхода, рассматривающего объект исследования в качестве черного ящика, информация о структуре и взаимодействии элементов которого практически отсутствует [2].

Основными факторами, сдерживающими развитие нейросетевого подхода в социологии, являются нестационарность и негладкость (даже иногда разрывность) социальных процессов, которые плохо отслеживаются при обучении нейрокомпьютерной сети.

Идеологически близким к нейросетевому подходу, но, как представляется, свободным от указанных недостатков, является метод локальной аппроксимации [3], простота программной реализации и определенная универсальность алгоритма которого делает возможным его распространение на исследования широкого класса социальных процессов и объектов.

Предлагаемый непараметрический метод локальной аппроксимации базируется на отказе от построения какой-либо аналитической модели и в своей основе имеет представление исследуемого процесса или объекта как некоторой базы данных с числовыми записями вида , где i=1,2,...N соответствует моменту календарного времени (или социального времени в терминологии [1]); векторы Xi и Yi – зафиксированным для этого момента значениям входных факторов и выходных переменных; N – общему количеству проведенных наблюдений на этапе сбора исследуемой информации.

В качестве входных переменных, предварительно нормированных, обычно используются основные характеристики, определяющие социально-экономический процесс (валовой производимый продукт, средняя заработная плата, демографические показа- тели и т.д.), а в качестве выходных – параметры, по отношению к которым строится прогноз (уровень безработицы, политическая активность населения, рост преступности, эффективность инвести- ций и т.п.). Следует заметить, что деление параметров на входные и выходные представляется условным и зависит в первую очередь от вида прогноза, так как алгоритм допускает взаимную замену входных параметров на выходные, что может использоваться, например, для анализа оптимальности принятых в прошлом управленческих решений.

В качестве источников информации для построения исходной базы данных модели могут быть использованы данные, извлекаемые из отчетов государственной и отраслевой статистик, и материалы специальных мероприятий по изучению социально-экономической ситуации (опросы населения, экспертов и т.д.).

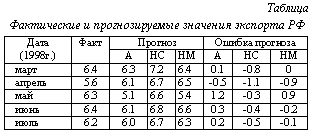
Для прогнозирования вектора выходных переменных при заданном векторе Х входных факторов используется метод "М ближайших соседей" [4] с применением метода (в данном случае локального) наименьших квадратов. Помимо процедуры прогнозирования, предложенный алгоритм может быть использован для определения отсутствующих значений при статистическом анализе данных с пропусками (статистическое наблюдение по неполным дан- ным [5]), если их восстановление необходимо для вычисления итоговых социальных оценок.

Программа, реализующая данный подход, на языке DELPHI 3 и может быть использована в качестве системы поддержки принятия решений (экспертной системы), структура которой в общем виде (см. рис.) содержит устройство ввода, позволяющее сформировать исходную базу данных, осуществлять нормировку данных и их пополнение. Блок "Набор решающих правил" осуществляет поиск векторов, ближайших, например в смысле евклидова расстояния, к вектору входных факторов Xj, для которого осуществляется прогноз, задает значения весовых коэффициентов, необходимых для вычисления указанного расстояния, подбирает аппроксимирующий полином, исходя из заданной точности модели, производит локальную аппроксимацию с вычислением прогнозируемого значения  [7] и при необходимости (вектор Yj может содержать и качественные переменные) вырабатывает конкретные рекомендации управленческого типа.

Иллюстрацией рассмотренного метода могут являться данные таблицы.

В первой колонке таблицы приведена календарная дата, во второй – фактическое значение экспорта РФ [6], в следующих трех колонках – прогнозируемые значения, рассчитанные аналитически с учетом сезонных колебаний группой прогнозирования высшей экономической школы, г. Москва (А) [6], с помощью нейросетевого подхода (НС) и с помощью непараметрической модели (НМ), последние три колонки содержат соответствующие ошибки прогноза (все значения приведены в млрд. долл. США).

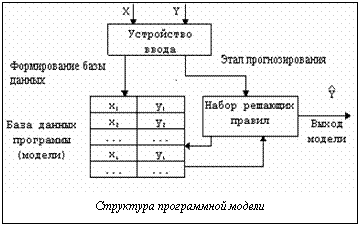Нейросетевой прогноз реализовывался с помощью нейроимитатора NeuroPro 0.1 (разработка Института вычислительного моделирования СО РАН, г. Красноярск) при структуре сети с одним скрытым слоем из трех нейронов и сигмоидной активационной функцией (структура сети и ее параметры оптимизировались). Как в данном случае, так и при использовании непараметрической модели, прогноз на один шаг вперед проводился по текущему и двум предыдущим значениям (экспорта). В обоих случаях для обучения использовались данные об экспорте за 1995-96 гг. и за январь-март 1997 г. (всего 27 значений). Как видно из приведенной таблицы, такая обобщенная характеристика прогноза, как сумма модулей ошибки, для метода А составляет в данном случае 2.3, для НС метода – 3.1, для метода НМ – 2.1, то есть в рассмотренной ситуации непараметрическая модель дает наилучшие результаты. Просчет других примеров (например прогноз динамики безработицы) также подтверждает эффективность метода.

Список литературы

1.   Давыдов А.А. Модель социального времени // Социологические исследования. – 1998. - №4.

2.   Бэстенс Д.-Э., Ван ден Берг В.-М., Вуд Д. Нейронные сети и финансовые рынки: принятие решения в торговых операциях. -М.: ТВП, 1997.

3.   Дли М.И., Круглов В.В. Применение метода локальной аппроксимации при построении алгоритмических мо- делей объектов управления // Вестник МЭИ. – 1998. - № 6. - С.108-111.

4.   Катковник В.Я. Непараметрическая идентификация и сглаживание данных. -М.: Наука, 1985.

5.   Чурилова Э.И. Некоторые методологические вопросы статистического анализа данных с пропусками // Вопросы статистики. - 1998. - № 5. - С.67-69.

6.   Российская Экономика: прогнозы и тенденции. – 1998. - № 61-63.

7.   Дли М.И. О формальном подходе к построению интерполяционного многочлена// Вестник МЭИ. - 1998. - № 4. -С.10-12.