Алгоритм факторизации матриц спектральной плотности
| Зотов М.Г. () - , Золотарев Ю.Г. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Задача факторизации является основной в направлении работ, в которых используется интегро-квадратичный критерий качества системы управления, и решается в пространстве операторов. Она тесно связана с решением матричных уравнений Винера-Хопфа. Более того, она является основной и при решении алгебраических уравнений Риккати методом, изложенным в [1]. Необходимость решения уравнений Риккати возникает при решении задач управления в пространстве состояний. Существует достаточно большое количество методов решения задачи факторизации. В [2] дан их обзор и приведена критика. В последующих работах [3,4] усилия были направлены на уменьшение сложности алгоритма решения, что крайне важно, так как решение матричного уравнения Винера-Хопфа, как и матричного уравнения Риккати, является центральным в САПР систем управления. И хотя эти усилия и снизили сложность решения, оно не было столь простым. В этих условиях альтернативные алгоритмы решения настоятельно необходимы. Пусть
квадратная матрица, элементы которой dkl(s) (k,l=1...n) являются дробно-рациональными функциями с вещественными коэффициентами комплексной переменной s. Будем считать, что ранг матрицы D(s) равен n. Рассмотрим задачу о факторизации матрицы D(s), иными словами, об определении таких матриц B(s) и C(s), элементами которых являются дробно-рациональные функции с вещественными коэффициентами bkl(s) и ckl(s), (k,l=1,...n), такие, что полюса элементов матриц B(s) и B-1(s) лежат только в левой полуплоскости, полюса элементов матриц C(s) и C-1(s) лежат только в правой полуплоскости и справедливо равенство D(s)=B(s)C(s). (2) Решение задачи 1) Факторизация полюсов. Каждый элемент dkl(s) матрицы D можно записать в виде Dkl(s)= где rkl(s), pkl(s), qkl(s) – полиномы комплексного переменного s с вещественными коэффициентами, причем все корни полиномов pkl(s) лежат только в левой полуплоскости, а все корни полиномов qkl(s) – только в правой. Обозначим pk(s) общее наименьшее кратное полиномов pk1(s), pk2(s),...pkn(s); через qk(s) – общее наименьшее кратное полиномов qk1(s), qk2(s), ... qkn(s). Введем диагональные матрицы
Рассмотрим матрицу (для простоты записи аргумент s опущен) D=P-1PDQQ-1 = =P-1 В ней A(s)=P(s)D(s)Q(s) (6) есть квадратная матрица, элементы которой являются многочленами с вещественными коэффициентами переменной s; P–1(s), Q–1(s) – диагональные матрицы с полюсами соответственно только в левой и только в правой полуплоскостях. На этом факторизация полюсов матрицы спектральной плотности завершена. Приступим к факторизации ее нулей. 2) Факторизация нулей (корни действительные). Рассмотрим задачу факторизации матрицы A(s) из (6), то есть задачу об определении матриц Вл(s) и Bп(s), элементами которых являются многочлены с вещественными коэффициентами относительно s, таких, что справедливо равенство
причем корни определителя матрицы Вл(s) лежат только в левой полуплоскости комплексного переменного s, а корни определителя матрицы Bп(s) – только в правой и на мнимой оси. В основе метода, предлагаемого для решения этой задачи, лежит утверждение о том, что если известен действительный или комплексный корень s0 определителя многочленной матрицы A(s), то ее можно представить в виде произведения двух многочленных матриц, определитель одной из которых будет иметь единственный корень s0, а определитель второй матрицы – все остальные корни определителя матрицы A(s). Проведя последовательно подобные представления для всех нулей определителя матрицы A(s), получим требуемое разложение (7). Пусть s0 является действительным корнем определителя матрицы A(s), то есть DA(s0))=0, и ранг матрицы A(s0) равен r. Тогда система уравнений
имеет фундаментальную систему решений, состоящую из k=n–r векторов (x11, x21,.....xn1),.... (x1k, x2k,......xnk). (9) В силу уравнений (8) функции
при s=s0 равны нулю. Следовательно, по теореме Безу многочлены cjl(s) делятся без остатка на (s–s0), и можно ввести многочлены
Введем матрицы
Покажем теперь, что если s0 есть действительный нуль определителя матрицы A(s), то эта матрица может быть представлена в виде A(s)=Nп(s)Lk(s)Hп–1. (13) Для этого составим произведение
что и доказывает утверждение. Так как без уменьшения общности можно считать, что фундаментальная система решений (9) может быть выбрана в виде: (1,0,...0,xk+1,1,...xn1), (0,1,0,...0,xk+1,2,...xn2 ),...(0,0,...0,1,xk+1,k,...xnk), то матрицы Hл и Hл–1 будут иметь вид:
Легко проверить, что произведение Hл на Hл–1, действительно есть единичная матрица. Рассмотрим случай, когда корень s0 расположен в левой полуплоскости. Если векторы (y11,y12,...y1n),...(yk1,yk2,...ykn) являются фундаментальной системой решений уравнений a11(s0)y1+a12(s0)y2+...+a1n(s0)yn=0, a1n(s0)y1+a2n(s0)y2+...+ann(s0)yn=0, (14) а многочлены dlj(s) определены равенствами
то, полагая
совершенно аналогично можно получить, что матрица A(s) представима в виде: A(s)=Hл–1Lk(s)Nл(s). (15) При факторизации матрицы A(s) нужно пользоваться представлением (13), если s0³0, и представлением (15), если s0<0. 3) Факторизация нулей (корни комплексные). Пусть теперь уравнение
имеет комплексный корень al1(s1)w1+al2(s1)w2+....+aln(s1)wn=0, l=1,2,...n (17) имеют фундаментальную систему решений (w1j=u1j+iv1j, w2j=u2j+iv2j,....wnj=unj+ivnj), j=1,...k. (18) Очевидно также, что и уравнения al1(s2)z1+al2(s2)z2+...+aln(s2)zn=0, l=1,2,...n (19) имеют фундаментальную систему решений (z1j=u1j–iv1j, z2j=u2j–iv2j,...znj=unj–ivnj), j=1,...k.(20) Определим линейные функции rlj(s)=xljs+ylj, l=1,...n, j=1,...k из условий rlj(s1)=wlj, rlj(s2)=zlj, l=1,...n, j=1,...k. (21) Учитывая (18) и (20), эти условия можно записать в виде
откуда
Положим flj(s)=al1(s)r1j(s)+al2(s)r2j(s)+...+aln(s)rnj(s), l=1,...n, j=1,..k. (23) В силу уравнений (17), (19) и условий (21) flj(s1)=0, flj(s2)=0, l=1,...n, j=1,...k и, следовательно, по теореме Безу многочлены flj(s) делятся без остатка на flj(s)=glj(s)g(s), l=1,...n, j=1,...k, (24) где glj(s) – многочлены с вещественными коэффициентами. Введем матрицу
Учитывая обозначения (23) и равенства (24), можно записать
и, следовательно, A(s)=Nп(s)Lk(s)Hп–1(s). (25) Отметим, что без уменьшения общности фундаментальную систему решений (18) можно выбрать в виде: (w1j=0,...wj-1, j=0, wjj=1,...wkj=0), (wk+1, j=uk+1+ivk+1, j,...wnj=unj+vnj), j=1,...k. Но тогда функции rlj(s) могут быть записаны в виде rlj=0,...rj–1, j=0, rjj=1, rj+1, j=0,...rkj=0, rk+1, j=ak+1, js+yk+1, j,... rnj(s)=anjs+ynj. Тогда матрицы Hп(s) и Hп–1(s) имеют вид:
Hп–1(s) является известной многочленной матрицей. Формула (25) показывает, что если известен комплексный корень Заметим, что составление матрицы A(s)=C(s)g(s)+D1s+E1, (26) где D1 и E1 постоянные матрицы, которые легко вычисляются по обобщенной схеме Горнера. Полагая в равенстве (25)
а решение системы уравнений (17)
равносильно решению системы с вещественными коэффициентами
Для того чтобы выделить множитель, соответствующий левому корню, проще всего транспонировать исходную матрицу и по вышеописанному алгоритму разложить ее. После получения искомого разложения провести обратное транспонирование. Пример 1. Пусть
Требуется факторизовать эту матрицу, то есть представить в виде (7). Корни определителя D(A(s)= = –s2+1 действительные s1,2=±1. Ранг матриц
равен r=1. Начнем с правого корня. Итак, s0=1 является действительным корнем определителя матрицы A(s). Система уравнений (8) имеет вид: 4x1 +4x2=0, 2x1 +2x2=0. Она имеет фундаментальную систему решений (9), состоящую из одного вектора (k=n–r): x11 =1, x21 = –1 и функции
Согласно соотношениям (10), (11) и (12) (при n=2, k=1) имеем:
Согласно (13) имеем:
Переобозначим Nп(s): Nп(s)=A(s). Найдем определитель матрицы A(s):
имеет нуль s0= –1, расположенный слева от мнимой оси. Ранг матрицы A(1) r=1. Составим для матрицы A(s) систему (14):
Она имеет фундаментальную систему решений y11= –1, y12=+1. Тогда
= ((s+2)–1)/(s+1)=+1, d12(s) = (a12(s)y11+a22(s)y12)/(s–s) = = (–(s+3)+2)/(s+1)= –1,
и по формуле (15) получим:
Таким образом,
Используя метод квадратного корня [5, с.135], найдем:
далее
откуда
Пример 2. Пусть
Уравнение D(A(s))=0 имеет комплексные корни: s1,2=1±2i, s3,4= –1±2i. Рассмотрим корни, лежащие в правой полуплоскости. Проведем фактроризацию матрицы A(s). С этой целью вычислим матрицу A(s1). По формуле (26)
По формуле (27)
Ранг матрицы A(1+2i) равен единице. Составим систему (17)
Она имеет решение: w11 =1, w21 = –i. Аналогично
и система
имеет решение z11=1, z21 =i. Согласно (22) находим x11=0, y11=1, x21= –0.5, y21 = 0.5. Следовательно, r11(s)=1, r21(s)= –0.5s+0.5. В соответствии с этим получим матрицы:
По формулам (23) имеем:
f21(s)=a21(s)r11+a22(s)r21= –4s–1+(s2–5)(–0.5s+0.5)= = – 0.5s3+0.5s2–1.5s–2.5 = –0,5(s+1)(s2–2s+5). Таким образом,
Откуда согласно (25) получим
Переобозначим: Nп(s)=A(s). Транспонируем A(s). Разложим его с использованием того же алгоритма. Результат разложения транспонируем обратно. В результате найдем:
Это и завершает факторизацию. Список литературы 1. Первозванский А.А. Курс теории автоматического управления.-М.: Наука, 1986. 2. Современная теория систем управления / Под ред. К.Т.Леондеса. - М.: Наука, 1965. 3. Зотов М.Г. Алгоритм факторизации матриц спектральной плотности // Изв. вузов. Приборостроение.- 1986. – №4. 4. Зотов М.Г. Улучшение алгоритма решения матричных уравнений Винера-Хопфа // Автометрия.-1994.- №1. 5. Калиткин Н.Н. Численные методы.-М.: Наука, 1978. |
http://swsys.ru/index.php?id=945&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Автоматизированная система принятия решений при стратегическом планировании устойчивого развития региона в условиях нечеткой информации
- Базовое программное обеспечение целостных компьютеризированных курсов в современной операционной обстановке
- Система моделирования и оценки эффективности торговых стратегий
- Компьютерные технологии сегодня: тенденции и прогнозы
- Информационная система оптимизации расписания доставки грузов от производителей сырья

 (1)
(1) (3)
(3)
 . (4)
. (4) . (5)
. (5) (7)
(7) (8)
(8)

 .
. (10)
(10) (11)
(11)



 =Nп(s)Lk(s),
=Nп(s)Lk(s),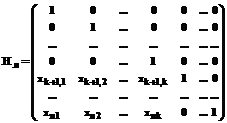 ,
, .
.


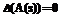 (16)
(16) из правой полуплоскости. Так как все многочлены akl(s) с вещественными коэффициентами, то уравнение (16) имеет и корень
из правой полуплоскости. Так как все многочлены akl(s) с вещественными коэффициентами, то уравнение (16) имеет и корень  . Допустим, что ранг матрицы A(s1) равен r и положим k=n–r. Тогда уравнения
. Допустим, что ранг матрицы A(s1) равен r и положим k=n–r. Тогда уравнения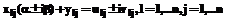 ,
, . (22)
. (22)
 , то есть
, то есть .
.


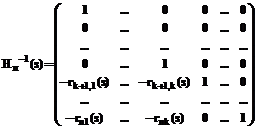 .
. определителя матрицы A(s), то в этой матрице может быть выделен правый множитель, являющийся многочленной матрицей. Аналогично может быть осуществлено и выделение из матрицы левого множителя.
определителя матрицы A(s), то в этой матрице может быть выделен правый множитель, являющийся многочленной матрицей. Аналогично может быть осуществлено и выделение из матрицы левого множителя. не требует операций с комплексными числами. Действительно, разделив A(s) на функцию g(s)=s2–2as + +a2 + b2, получим
не требует операций с комплексными числами. Действительно, разделив A(s) на функцию g(s)=s2–2as + +a2 + b2, получим , получим для
, получим для  , (27)
, (27)

 .
.
 при s=1 равны нулю. Составим многочлены:
при s=1 равны нулю. Составим многочлены:









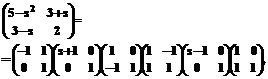





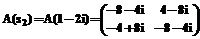


 = –s2+2s–5,
= –s2+2s–5,

 ,
,