Обобщенная локально-аппроксимационная модель динамического объекта
| Дли М.И. (midli@mail.ru) - Филиал Московского энергетического института (технического университета) в г. Смоленске (профессор, зам. директора по научной работе), г. Смоленск, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Как было показано в [1,2], локально-аппроксимационная (программная) модель представляет собой инструмент для прогнозирования выхода объекта произвольной сложности. Ее основой является база данных, записи которой хранят информацию о конкретных наборах входных и выходных переменных, полученную на этапе обучения модели. Прогноз выхода осуществляется с применением локальной аппроксимации (интерполяции): по предъявляемому набору входных переменных в базе данных отыскивается ряд ближайших подобных наборов, по которым простейшей аппроксимационной (интерполяционной) формулой (линейной или квадратичной) и рассчитывается прогнозируемое значение. Основные идеи и предпосылки алгоритма рассмотрим для простоты на примере стационарного непрерывного одномерного динамического объекта, имеющего скалярные вход u(t) и выход y(t) (рис.1), хотя предлагаемый подход и допускает расширение на нестационарные и многомерные динамические объекты. Предположим, что регистрация входного и выходного сигналов как на этапе изучения, так и в режиме нормального функционирования объекта происходит в дискретные эквидестантные моменты времени ti, интервал между которыми Dt значительно меньше постоянных времени объекта, так что в распоряжении пользователя находятся значения = . Решение задачи построения обобщенной программной модели динамического объекта, позволяющего прогнозировать его выход только по значениям входного сигнала, может быть получено, например, в следующей постановке.
Воспользуемся аппроксимационным представлением w(t):
где n – заданное число; {wj(t)} – известные базисные функции; aj – коэффициенты разложения. Полагая начальные условия в ЛДЗ нулевыми, на основании (1) для сигнала z(t) можно запи- сать [3]:
где В предположении, что функция h(t) является гладкой (дифференцируемой), в любой локальной области ее можно представить как
где z* – некоторая базовая точка. Введем здесь следующие обозначения:
Тогда (4) можно переписать в виде
или с учетом (2) в виде
где
Из (6) следует, что прогнозируемое значение выхода объекта можно представить соотношением
где в данном случае По сравнению с (6) в последней формуле отсутствует свободный член (слагаемое с0). Это обстоятельство при последующем определении вектора c приведет к смещенности его оценки, но в данном случае, поскольку речь идет о прогнозе, а не об определении истинной модели, такая смещенность не имеет значения. Заметим, что эти выражения не очень удобны для численных расчетов (так, при их использовании необходимо хранить все значения входного сигнала и т.п.), но с вычислительной точки зрения ситуацию можно упростить, если использовать в качестве базисных wj(t) функции Лагерра [3,4] вида
где a – параметр функций, и применить результаты следующей теоремы. Теорема1. Если выбранный базис
таков, что в области допустимых значений аргумента
где
(I обозначает единичную матрицу), то для вектора
причем матрица A(t) и вектор b(t) определяются выражениями
Доказательство. Решение уравнения (11) при нулевых начальных условиях имеет вид [5]
где В соответствии же с выражениями (3) и с условием (9) имеем
При выполнении равенства (12) формулы (14) и (16) становятся подобными, а учитывая, что
откуда получаем формулу (13). Теорема доказана. Следует отметить, что для стационарных объектов весовая функция (импульсная переходная характеристика) зависит только от разности аргументов t-t. Рассматривая эту разность как новый аргумент и учитывая, что для стационарных объектов, описываемых выражением (11), матрица A не зависит от времени, можно показать, что функции, входящие в выражения (9), (12), (13), будут являться только функциями этого нового аргумента и примут вид (при обозначении этого аргумента для простоты тоже через t):
Отметим также, что условия теоремы всегда выполняются, если набор базисных функций представляет собой полный набор решений линейного дифференциального уравнения. Условиям приведенной теоремы удовлетворяет, в частности, набор функций Лагерра (8), для которого:
При переходе к дискретному времени ti=i×Dt расчет значений xi в данном случае удобно осуществлять по рекуррентной процедуре [5]
С учетом изложенного процедуру построения обобщенной локально-аппроксимационной модели можно описать следующим образом.
По формулам (19)-(21) рассчитываются значения xi, формируется начальная база модели в виде матрицы U со строками < 2. Для каждой вновь вводимой экспериментальной точки (uk ,yk) рассчитывается xk и формируется вектор расстояний, например евклидовых или Хэмминга
3. Из матрицы U отбирается М строк, наиболее близких в смысле выбранного расстояния к строке <
4. По соотношению
рассчитывается прогнозируемое значение выхода объекта. 5. Проверяется неравенство
при выполнении которого матрица U пополняется строкой < 6. Проверяется принятое правило останова. При его невыполнении – переход к п. 2 процедуры. При выполнении – переход к следующему пункту. 7. Конец процедуры. Задаваемая исходная информация: параметры М, d, n, a (параметр функций Лагерра). Использование модели (при сформированной базе модели U) сводится к реализации п.п.2-4. Пример. Объект имитировался уравнениями
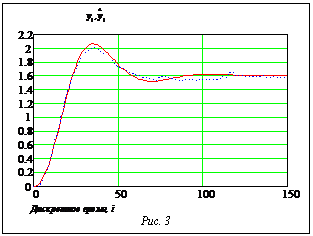
при шаге дискретизации Dt=0.1 с. При построении в соответствии с приведенной процедурой (при значениях параметров M=12, d=0.1, n=4, a=0.6 c–1 и идентифицирующим сигналом типа дискретного белого шума uiÎ(0,2)) локально-аппроксимационной модели была сформирована матрица U, содержащая 5 столбцов (соответствующих x1¸x4 и y) и 18 строк. Диагностическая проверка модели при использовании u(t)=1[t] дала результат, приведенный на рисунке 3 (пунктиром обозначена кривая По-видимому, этот результат можно считать удовлетворительным. Список литературы 1. Дли М.И., Круглов В.В. Построение и применение информационных моделей сложных объектов, основанных на методе локальной аппроксимации// Цифровая обработка информации и управление в чрезвычайных ситуациях// Матер. I Междунар. конф. - Т.1. - Минск: Ин-т техн. кибернетики НАН Беларуси. - 1998. - С.62-65. 2. Дли М.И., Круглов В.В. Применение метода локальной аппроксимации при построении алгоритмических моде- лей объектов управления// Вестник МЭИ. - 1998. - №6. - С.109-111. 3. Эйкофф П. Основы идентификации систем управления. - М.: Мир, 1975. 4. Планирование эксперимента в исследовании технологических процессов /К.Хартман, Э.Лецкий, В.Шефер и др. - М.: Мир, 1977. 5. Директор С., Рорер Р. Введение в теорию систем. - М.: Мир, 1974. |
http://swsys.ru/index.php?id=946&lang=%E2%8C%A9%3Den&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Подход к выбору оптимального маршрута при перевозке крупногабаритных грузов на основе нейросетевых технологий
- Методы восстановления пропусков в массивах данных
- Интеллектуальные хранилища данных в системах государственного управления
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам

 Пусть в структуре на рисунке 1 динамический объект может быть представлен состоящим из последовательно соединенных линейного динамического звена (ЛДЗ) и статического нелинейного элемента (НЭ), как это представлено на рисунке 2.
Пусть в структуре на рисунке 1 динамический объект может быть представлен состоящим из последовательно соединенных линейного динамического звена (ЛДЗ) и статического нелинейного элемента (НЭ), как это представлено на рисунке 2.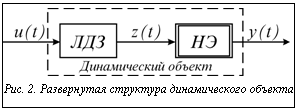 Пусть линейное динамическое звено характеризуется импульсной переходной характеристикой w(t), а нелинейный элемент – функцией h(z). Предполагается, естественно, что w(t) и h(z) неизвестны.
Пусть линейное динамическое звено характеризуется импульсной переходной характеристикой w(t), а нелинейный элемент – функцией h(z). Предполагается, естественно, что w(t) и h(z) неизвестны.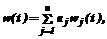 (1)
(1)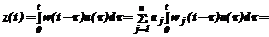
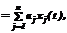 (2)
(2)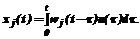 (3)
(3)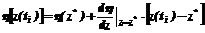 , (4)
, (4)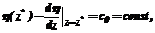
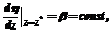
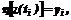
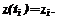
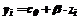 (5)
(5)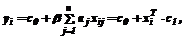 (6)
(6)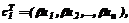
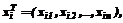
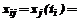
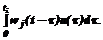
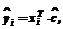 (7)
(7)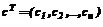 .
.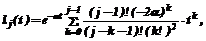 j=1,2,...,n, (8)
j=1,2,...,n, (8)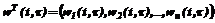
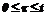 возможно представление
возможно представление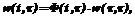 (9)
(9)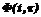 – некоторая матрица, обладающая свойствами переходной матрицы [5]
– некоторая матрица, обладающая свойствами переходной матрицы [5]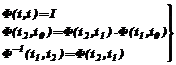 (10)
(10)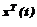
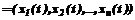 с компонентами xj(t), задаваемыми (3), справедливо дифференциальное уравнение
с компонентами xj(t), задаваемыми (3), справедливо дифференциальное уравнение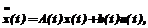 (11)
(11)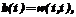 (12)
(12)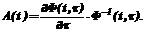 (13)
(13)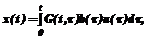 (14)
(14)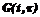 – переходная матрица системы (11).
– переходная матрица системы (11).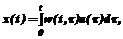 (15)
(15)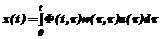 . (16)
. (16)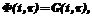 то есть матрица
то есть матрица 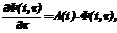 (17)
(17)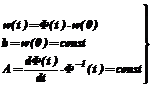 . (18)
. (18)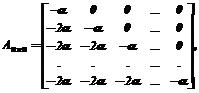 (19)
(19)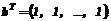 (20)
(20)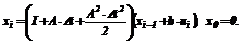 (21)
(21) 1. Производится начальный эксперимент, в ходе которого фиксируются N пар значений (ui ,yi).
1. Производится начальный эксперимент, в ходе которого фиксируются N пар значений (ui ,yi).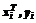 >.
>.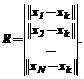
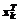 >. Формируется матрица F и вектор y вида:
>. Формируется матрица F и вектор y вида: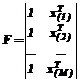 ,
, 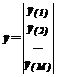 .
.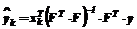 (22)
(22)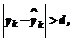
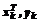 >, в противном случае матрица U не изменяется.
>, в противном случае матрица U не изменяется.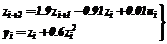 (23)
(23) ).
).