В многономенклатурных химических производствах из-за структурных модификаций ассортимента выпускаемой продукции часто возникает так называемая задача размещения технологических процессов ее получения на действующих установках, функционирующих в дискретном режиме. Содержательно задача состоит в установлении наличия необходимого технологического оборудования, материалопроводов, резервов мощности и в оптимальном распределении технологических процессов по аппаратурным схемам.
Пусть требуется разместить множество технологических процессов получения продуктов модифицированного ассортимента на аппаратурных схемах действующего производства. Аппаратурная схема Gi(Ai,Ui); , где Ai – аппаратурный состав, характеризующийся векторами значений параметров Xi = (xi1, xi2, ..., xin), а Ui – материалопроводы, характиризующиеся векторами значений параметров Zi = (zi1, zi2, ..., zim). Значения Xi и Zi выделяют некоторые замкнутые области Ei гиперпространства параметров. Структурная модель аппаратурной схемы Gi имеет вид графа Gi¢(Ai¢,Ui¢ ), в котором Ai¢ – множество вершин, а Ui¢ – множество дуг. Ориентация графа Gi¢ задается отображением Wi: Ui¢ ® Ai¢ ´ Ai¢, в результате которого получается ориентированный граф GiW= (Ai¢, Wi, Ui¢) [1] .
, где Ai – аппаратурный состав, характеризующийся векторами значений параметров Xi = (xi1, xi2, ..., xin), а Ui – материалопроводы, характиризующиеся векторами значений параметров Zi = (zi1, zi2, ..., zim). Значения Xi и Zi выделяют некоторые замкнутые области Ei гиперпространства параметров. Структурная модель аппаратурной схемы Gi имеет вид графа Gi¢(Ai¢,Ui¢ ), в котором Ai¢ – множество вершин, а Ui¢ – множество дуг. Ориентация графа Gi¢ задается отображением Wi: Ui¢ ® Ai¢ ´ Ai¢, в результате которого получается ориентированный граф GiW= (Ai¢, Wi, Ui¢) [1] .
 По виду материальных связей между аппаратами различают трубопроводные и беструбопроводные аппаратурные схемы. В первых схемах транспорт порций промежуточных продуктов осуществляется по технологическим трубопроводам из подающих аппаратов в принимающие либо непосредственно, либо через демпфирующие емкости-накопители; во вторых схемах трубопроводные связи между аппаратами отсутствуют, а перемещаются технологические аппараты. Структурной моделью беструбопроводных систем является сильно связный граф. На рисунке 1 приведен пример графов, являющихся структурными моделями трубопроводной и беструбопроводной систем.
По виду материальных связей между аппаратами различают трубопроводные и беструбопроводные аппаратурные схемы. В первых схемах транспорт порций промежуточных продуктов осуществляется по технологическим трубопроводам из подающих аппаратов в принимающие либо непосредственно, либо через демпфирующие емкости-накопители; во вторых схемах трубопроводные связи между аппаратами отсутствуют, а перемещаются технологические аппараты. Структурной моделью беструбопроводных систем является сильно связный граф. На рисунке 1 приведен пример графов, являющихся структурными моделями трубопроводной и беструбопроводной систем.
Многостадийный технологический процесс Sj(Oj, Rj);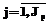 , где Oj – технологические стадии, характеризующиеся значениями векторов параметров Yj=(yj1,yj2,...,yjn), а Rj – материальные потоки, характеризующиеся параметрами Wj = (wj1, wj2, ..., wjm). Множество значений Yj и Wj выделяют области Fj гиперпространства параметров. Структурной моделью технологического процесса Sj является граф Sj¢(Oj¢, Rj¢), где Oj¢ – множество вершин, Rj¢ – множество дуг. Ориентация графа Sj¢ задается отображением Yj : Rj¢ ® Oj¢ x Oj¢, в результате которого получается ориентированный граф SjY¢= (Oj¢, Y j, Rj¢) [1]. Принципиально разместить процесс Sj на аппаратурной схеме Gi возможно, если граф SjY¢(Oj¢, Y, Rj¢) является подграфом графа GjW¢(Ai¢, W, Ui¢), то есть SjW¢ Í GiW¢, а область гиперпространства Fj режимных параметров Yj является подмножеством области Ei гиперпространства конструкционных параметров, то есть Fj Í Ei. На рисунке 2 приведены графы G¢, S1¢, S2¢, S3¢. Графы S1¢, S2¢ являются подграфами графа G¢, а граф S3¢ не является таковым.
, где Oj – технологические стадии, характеризующиеся значениями векторов параметров Yj=(yj1,yj2,...,yjn), а Rj – материальные потоки, характеризующиеся параметрами Wj = (wj1, wj2, ..., wjm). Множество значений Yj и Wj выделяют области Fj гиперпространства параметров. Структурной моделью технологического процесса Sj является граф Sj¢(Oj¢, Rj¢), где Oj¢ – множество вершин, Rj¢ – множество дуг. Ориентация графа Sj¢ задается отображением Yj : Rj¢ ® Oj¢ x Oj¢, в результате которого получается ориентированный граф SjY¢= (Oj¢, Y j, Rj¢) [1]. Принципиально разместить процесс Sj на аппаратурной схеме Gi возможно, если граф SjY¢(Oj¢, Y, Rj¢) является подграфом графа GjW¢(Ai¢, W, Ui¢), то есть SjW¢ Í GiW¢, а область гиперпространства Fj режимных параметров Yj является подмножеством области Ei гиперпространства конструкционных параметров, то есть Fj Í Ei. На рисунке 2 приведены графы G¢, S1¢, S2¢, S3¢. Графы S1¢, S2¢ являются подграфами графа G¢, а граф S3¢ не является таковым.
Для определения реальной возможности размещения новых технологических процессов на аппаратурных схемах действующего производства необходимо наличие свободных мощностей.
В общем случае возможны множества допустимых вариантов размещения; для нахождения оптимального варианта необходимо решить модифицированную задачу о назначениях, которая имеет следующий вид:
 , (1)
, (1)
при  , (2)
, (2)
 , (3)
, (3)
 , (4)
, (4)
 , (5)
, (5)
 , (6)
, (6)
 . (7)
. (7)
Ограничения (2-5) имеют следующий смысл: (2) – количество технологических схем, на которых может быть размещен каждый продукт, не должно превышать их наличного количества в группе; (3) – количество продуктов, размещаемых на каждой схеме, не должно превышать общего числа продуктов в группе; (4) – объем выпуска каждого продукта не должен превышать заданного значения; (5) – все продукты ассортимента должны быть произведены в течение фонда времени T0.
Для трубопроводных систем, в которых технологические аппараты взаимодействуют непосредственно:
 , (8)
, (8)
 , (9)
, (9)
 . (10)
. (10)

Рис. 2. Графы аппаратурной (G¢) и технологических (S¢1,S¢2,S¢3) схем
Для размещения технологических процессов в беструбопроводных аппаратурных схемах выполнение условий (6)-(7) означает наличие и адекватность только аппаратурного состава схемы.
Для трубопроводных систем, в которых технологические аппараты взаимодействуют через вспомогательные емкости-накопители, справедливы следующие дополнительные условия:
 , (11)
, (11)
 ,(12)
,(12)

Рис. 3. Графики загрузки (1), разгрузки (2,2¢,2²) демпфирующей емкости и изменения объема реакционной массы в ней (3,3¢,3²) при различных значениях Dt
где  . (13)
. (13)
Вид функций  и, следовательно, функции
и, следовательно, функции  определяется режимом работы взаимодействующих технологических аппаратов, который может быть непрерывным или периодическим, а также способом разгрузки подающих аппаратов в емкость и загрузки принимающих аппаратов из емкости [2]. При периодическом режиме работы взаимодействующих аппаратов и осуществлении транспортных операций насосом эти функции имеют следующий вид (рис. 3).
определяется режимом работы взаимодействующих технологических аппаратов, который может быть непрерывным или периодическим, а также способом разгрузки подающих аппаратов в емкость и загрузки принимающих аппаратов из емкости [2]. При периодическом режиме работы взаимодействующих аппаратов и осуществлении транспортных операций насосом эти функции имеют следующий вид (рис. 3).
 , (14)
, (14)
 ,(15)
,(15)
 , (16)
, (16)
 , (17)
, (17)
 ,(18)
,(18)
 , (19)
, (19)
 . (20)
. (20)
Правило изменения n, n¢ в формулах (14-15) изложено ниже.
В общем случае  является периодической разрывной мультимодальной функцией, удовлетворяющей условию Дирихле; функции uijkmax(
является периодической разрывной мультимодальной функцией, удовлетворяющей условию Дирихле; функции uijkmax( )=
)= , uijkmin(
, uijkmin( ) =
) =  – монотонно
– монотонно возрастающие по
возрастающие по  (рис. 4), а функция
(рис. 4), а функция

дискретна по j.

Рис. 4. Зависимость объемов реакционной массы в
демпфирующей емкости от интервала времени между моментами первых загрузки и разгрузки
Описание алгоритма
Задача размещения технологических процессов на действующем оборудовании решается в два этапа. Первый этап образует модифицированный алгоритм покрытия графа, обеспечивающий допустимое распределение продуктов по технологическому оборудованию [3]. Второй этап заключается в поиске оптимального варианта их распределения, и представляет собой модифицированный алгоритм задачи о назначениях.
Модификация алгоритма покрытия графа заключается в оценке соответствия значений параметров аппаратов значениям параметров технологического процесса, осуществляемого по его соответствующим моделям.
Для каждого графа Gi¢ определим, является ли граф Sj¢ его подграфом. Содержательно это эквивалентно группировке продуктов модифицированного ассортимента, при которой определены группы, отнесенные к каждой из аппаратурных схем. Таким образом, ассортимент P оказывается декомпозирован на пересекающиеся классы Pi, где Pi – группа продуктов, которая принципиально может быть произведена в аппаратурной схеме i. Тогда:
 . (21)
. (21)
Зная объем выпуска каждого продукта, оставшегося в ассортименте, рассчитаем интервал времени Ti, в течение которого аппаратурная схема i свободна; если продукты выпускаются последовательно, то
 . (22)
. (22)
Тогда Ti представляет интервал времени, в течение которого на схеме i могут производиться продукты, вновь включенные в ассортимент.
Алгоритм второго этапа зависит от типа аппаратурной структуры химико-технологической системы, на которой размещаются технологические процессы: при непосредственной связи аппаратов он представляет собой одноуровневый алгоритм, а при наличии емкостей двухуровневый.
Задача оптимального размещения (1)-(10) в системах с непосредственной связью аппаратов является дискретной задачей, содержащей дискретные переменные b и целочисленные a, а аналогичная задача (1)-(20) для систем, содержащих демпфирующие емкости – частично-дискретной задачей, содержащей, кроме переменных b и a, непрерывные переменные Dt.
Произведем замену дискретных переменных b [4]:
 . (23)
. (23)
С учетом замены переменных (23) критерий оптимальности (1) примет вид:
 (24)
(24)
при ограничениях (2)-(10) и условии
 , (25)
, (25)
являющемся аналогом ограничения (4) для систем с непосредственным взаимодействием аппаратов и ограничениях (2,3,5-7,11-20) – при наличии в системе емкостей.
Замена дискретных переменных целочисленными позволяет применить для решения задачи размещения в системах с непосредственной связью аппаратов алгоритм квадратичного целочисленного программирования [5], а при наличии в системе демпфирующих емкостей – двухуровневый алгоритм, верхний уровень которого является алгоритмом квадратичного целочисленного программирования, а нижний – алгоритмом оптимизации по непрерывным переменным Dt.
Нижний уровень алгоритма заключается в определении экстремальных значений объема реакционной массы, содержащейся в демпфирующей емкости в течение ее технологического цикла и такого значения Dt, при котором максимум был бы минимальным, а минимум равным нулю. Экстремальные значения функции u(t, Dt) ищутся в пределах ее периода Q, который равен аликвотной части продолжительности технологических циклов группы взаимодействующих аппаратов. Для обеспечения конечности алгоритма расчета Q масштабированием по времени заменим действительные числа  и
и  их натуральными эквивалентами
их натуральными эквивалентами  и
и  , что дает возможность рассчитывать период Q как наименьшее общее кратное
, что дает возможность рассчитывать период Q как наименьшее общее кратное  и
и  . Последнее определяется по формуле:
. Последнее определяется по формуле:
 , (26)
, (26)
где  – наибольший общий делитель
– наибольший общий делитель  и
и  . Последний может быть рассчитан по алгоритму Евклида.
. Последний может быть рассчитан по алгоритму Евклида.
Значения функции  рассчитываются по следующему алгоритму. Так как
рассчитываются по следующему алгоритму. Так как  и оптимальное значение
и оптимальное значение  должно удовлетворять условию
должно удовлетворять условию


 , (27)
, (27)
то  находится методом деления интервала
находится методом деления интервала  в отношении золотого сечения; при этом число n загрузок демпфирующей емкости до момента ее первой разгрузки определяется условием:
в отношении золотого сечения; при этом число n загрузок демпфирующей емкости до момента ее первой разгрузки определяется условием:
 . (28)
. (28)
Очевидно, что при этом n¢=1.
Далее значения функции  рассчитываются на интервале
рассчитываются на интервале  , а содержащиеся в формулах (14),(15) величины n, n¢ изменяются в соответствии с алгоритмом:
, а содержащиеся в формулах (14),(15) величины n, n¢ изменяются в соответствии с алгоритмом:
n=n+1, если  , (29)
, (29)
n¢=n+1, если  . (30)
. (30)
Так как  в общем случае мультимодальная кусочно-непрерывная функция, удовлетворяющая условию Дирихле, то вместо экстремума в обычном смысле, который для функций этого класса не определен, будем искать обобщенный экстремум в виде последовательности аппроксимационных экстремумов методом аппроксимационного градиента [5], в результате которого найдем:
в общем случае мультимодальная кусочно-непрерывная функция, удовлетворяющая условию Дирихле, то вместо экстремума в обычном смысле, который для функций этого класса не определен, будем искать обобщенный экстремум в виде последовательности аппроксимационных экстремумов методом аппроксимационного градиента [5], в результате которого найдем:
 , (31)
, (31)
 . (32)
. (32)
В целях унификации алгоритма оптимизации вместо  будем искать
будем искать
 . (33)
. (33)
Затем найдем

Оба эти условия достигаются при
 . (36)
. (36)
Описанная выше процедура повторяется для всех продуктов системы с целью поиска
 (37)
(37)
для оптимизации объема демпфирующих емкостей.
Разработанный комплекс алгоритмов гарантирует оптимальное размещение технологических процессов при структурных модификациях ассортимента продукции и изменениях конъюнктуры потребительского рынка, что во многих случаях позволяет избежать разработки и проектирования новых производств или реконструкции действующих. Развиваемый подход ориентирован на детерминированные технологические системы и не учитывает характерную для некоторых производств неопределенность исходной информации и параметров моделей. Однако при наличии необходимого статистического материала и при незначительной модификации разработанный комплекс алгоритмов может быть применен при решении задачи размещения в условиях неопределенности.
Обозначения в формулах
а – количество значений дискретной переменной;
c – стоимость получения продукта;
g – массовый размер порции продукта;
I – количество аппаратурных схем;
IGi – количество стадий в аппаратурной схеме;
i – текущий номер аппаратурной схемы;
Ij – количество схем, на которых может быть размещен продукт j;
Ji – количество продуктов, которые могут быть размещены на схеме i;
Jp – количество размещаемых технологических процессов;
j – текущий номер технологического процесса;
k – текущий номер стадии технологического процесса;
m – размерность пространства конструкционных параметров технологических трубопроводов и материальных потоков;
N – количество параллельных аппаратов;
n – размерность пространства конструкционных параметров аппаратов и режимных параметров технологических процессов;
Q – объем выпуска продукта;
s – материальный индекс;
t0 – момент начала первой загрузки емкости-накопителя;
t – время;
U – объем емкости-накопителя;
u – объем реакционной массы в емкости-накопителе;
u* – максимальный объем реакционной массы в емкости-накопителе;
 – функция загрузки емкости-накопителя;
– функция загрузки емкости-накопителя;
 – функция разгрузки емкости-накопителя;
– функция разгрузки емкости-накопителя;
V – объем технологического аппарата;
a – бинарные переменные;
b – количество порций продукта;
Q – период функции  ;
;
t – продолжительность цикла аппарата;
 – продолжительность транспортной операции;
– продолжительность транспортной операции;
 – продолжительность технологической операции;
– продолжительность технологической операции;
 – продолжительность цикла установки;
– продолжительность цикла установки;
 – интервал времени между первыми загрузкой и разгрузкой емкости-накопителя;
– интервал времени между первыми загрузкой и разгрузкой емкости-накопителя;
 – продолжительность технологического цикла аппарата периодического действия;
– продолжительность технологического цикла аппарата периодического действия;
 – объем порции продукта, поступающего из подающего аппарата в емкость-накопитель;
– объем порции продукта, поступающего из подающего аппарата в емкость-накопитель;
 – объем порции реакционной массы, выгружаемой из емкости-накопителя в принимающий аппарат;
– объем порции реакционной массы, выгружаемой из емкости-накопителя в принимающий аппарат;
 – минимальное и максимальное значение коэффициента заполнения объема аппарата.
– минимальное и максимальное значение коэффициента заполнения объема аппарата.
Список литературы
1. Лескин А.А. Алгебраические основы задачи выбора оборудования гибких производственных систем. - В кн.: Проблемы автоматизации и производственных процессов. - М.: Наука, 1985.- 262 с.
2. Макаров В.В. // Теоретич.осн.хим.технол. - 1994. - Т. 28. - №5. - С.453-464.
3. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. - М.: Мир, 1982.- 416 с.
4. Хохлюк В.И. Параллельные алгоритмы целочисленной оптимизации. - М.: Радио и связь, 1987.- 224 с.
5. Pierce J.F., Crowston W.B. // Nav.Res.Log.Quart.-1971,V.18, №1, p.1-36.
6. Батухтин В.Д., Майборода Л.А. Оптимизация разрывных функций.- М.: Наука, 1984. -208 с.

 , где Ai – аппаратурный состав, характеризующийся векторами значений параметров Xi = (xi1, xi2, ..., xin), а Ui – материалопроводы, характиризующиеся векторами значений параметров Zi = (zi1, zi2, ..., zim). Значения Xi и Zi выделяют некоторые замкнутые области Ei гиперпространства параметров. Структурная модель аппаратурной схемы Gi имеет вид графа Gi¢(Ai¢,Ui¢ ), в котором Ai¢ – множество вершин, а Ui¢ – множество дуг. Ориентация графа Gi¢ задается отображением Wi: Ui¢ ® Ai¢ ´ Ai¢, в результате которого получается ориентированный граф GiW= (Ai¢, Wi, Ui¢) [1] .
, где Ai – аппаратурный состав, характеризующийся векторами значений параметров Xi = (xi1, xi2, ..., xin), а Ui – материалопроводы, характиризующиеся векторами значений параметров Zi = (zi1, zi2, ..., zim). Значения Xi и Zi выделяют некоторые замкнутые области Ei гиперпространства параметров. Структурная модель аппаратурной схемы Gi имеет вид графа Gi¢(Ai¢,Ui¢ ), в котором Ai¢ – множество вершин, а Ui¢ – множество дуг. Ориентация графа Gi¢ задается отображением Wi: Ui¢ ® Ai¢ ´ Ai¢, в результате которого получается ориентированный граф GiW= (Ai¢, Wi, Ui¢) [1] .
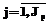 , где Oj – технологические стадии, характеризующиеся значениями векторов параметров Yj=(yj1,yj2,...,yjn), а Rj – материальные потоки, характеризующиеся параметрами Wj = (wj1, wj2, ..., wjm). Множество значений Yj и Wj выделяют области Fj гиперпространства параметров. Структурной моделью технологического процесса Sj является граф Sj¢(Oj¢, Rj¢), где Oj¢ – множество вершин, Rj¢ – множество дуг. Ориентация графа Sj¢ задается отображением Yj : Rj¢ ® Oj¢ x Oj¢, в результате которого получается ориентированный граф SjY¢= (Oj¢, Y j, Rj¢) [1]. Принципиально разместить процесс Sj на аппаратурной схеме Gi возможно, если граф SjY¢(Oj¢, Y, Rj¢) является подграфом графа GjW¢(Ai¢, W, Ui¢), то есть SjW¢ Í GiW¢, а область гиперпространства Fj режимных параметров Yj является подмножеством области Ei гиперпространства конструкционных параметров, то есть Fj Í Ei. На рисунке 2 приведены графы G¢, S1¢, S2¢, S3¢. Графы S1¢, S2¢ являются подграфами графа G¢, а граф S3¢ не является таковым.
, где Oj – технологические стадии, характеризующиеся значениями векторов параметров Yj=(yj1,yj2,...,yjn), а Rj – материальные потоки, характеризующиеся параметрами Wj = (wj1, wj2, ..., wjm). Множество значений Yj и Wj выделяют области Fj гиперпространства параметров. Структурной моделью технологического процесса Sj является граф Sj¢(Oj¢, Rj¢), где Oj¢ – множество вершин, Rj¢ – множество дуг. Ориентация графа Sj¢ задается отображением Yj : Rj¢ ® Oj¢ x Oj¢, в результате которого получается ориентированный граф SjY¢= (Oj¢, Y j, Rj¢) [1]. Принципиально разместить процесс Sj на аппаратурной схеме Gi возможно, если граф SjY¢(Oj¢, Y, Rj¢) является подграфом графа GjW¢(Ai¢, W, Ui¢), то есть SjW¢ Í GiW¢, а область гиперпространства Fj режимных параметров Yj является подмножеством области Ei гиперпространства конструкционных параметров, то есть Fj Í Ei. На рисунке 2 приведены графы G¢, S1¢, S2¢, S3¢. Графы S1¢, S2¢ являются подграфами графа G¢, а граф S3¢ не является таковым. , (1)
, (1) , (2)
, (2) , (3)
, (3) , (4)
, (4) , (5)
, (5) , (6)
, (6) . (7)
. (7) , (8)
, (8) , (9)
, (9) . (10)
. (10)
 , (11)
, (11) ,(12)
,(12)
 . (13)
. (13) и, следовательно, функции
и, следовательно, функции  определяется режимом работы взаимодействующих технологических аппаратов, который может быть непрерывным или периодическим, а также способом разгрузки подающих аппаратов в емкость и загрузки принимающих аппаратов из емкости [2]. При периодическом режиме работы взаимодействующих аппаратов и осуществлении транспортных операций насосом эти функции имеют следующий вид (рис. 3).
определяется режимом работы взаимодействующих технологических аппаратов, который может быть непрерывным или периодическим, а также способом разгрузки подающих аппаратов в емкость и загрузки принимающих аппаратов из емкости [2]. При периодическом режиме работы взаимодействующих аппаратов и осуществлении транспортных операций насосом эти функции имеют следующий вид (рис. 3). , (14)
, (14) ,(15)
,(15) , (16)
, (16) , (17)
, (17) ,(18)
,(18) , (19)
, (19) . (20)
. (20) является периодической разрывной мультимодальной функцией, удовлетворяющей условию Дирихле; функции uijkmax(
является периодической разрывной мультимодальной функцией, удовлетворяющей условию Дирихле; функции uijkmax( )=
)= , uijkmin(
, uijkmin( – монотонно
– монотонно возрастающие по
возрастающие по 

 . (21)
. (21) . (22)
. (22) . (23)
. (23) (24)
(24) , (25)
, (25) и
и  их натуральными эквивалентами
их натуральными эквивалентами  и
и  , что дает возможность рассчитывать период Q как наименьшее общее кратное
, что дает возможность рассчитывать период Q как наименьшее общее кратное  , (26)
, (26) – наибольший общий делитель
– наибольший общий делитель  рассчитываются по следующему алгоритму. Так как
рассчитываются по следующему алгоритму. Так как  и оптимальное значение
и оптимальное значение  должно удовлетворять условию
должно удовлетворять условию

 , (27)
, (27) находится методом деления интервала
находится методом деления интервала  в отношении золотого сечения; при этом число n загрузок демпфирующей емкости до момента ее первой разгрузки определяется условием:
в отношении золотого сечения; при этом число n загрузок демпфирующей емкости до момента ее первой разгрузки определяется условием: . (28)
. (28) , а содержащиеся в формулах (14),(15) величины n, n¢ изменяются в соответствии с алгоритмом:
, а содержащиеся в формулах (14),(15) величины n, n¢ изменяются в соответствии с алгоритмом: , (29)
, (29) . (30)
. (30) , (31)
, (31) . (32)
. (32) будем искать
будем искать . (33)
. (33)
 . (36)
. (36) (37)
(37) – функция загрузки емкости-накопителя;
– функция загрузки емкости-накопителя; – функция разгрузки емкости-накопителя;
– функция разгрузки емкости-накопителя; ;
; – продолжительность транспортной операции;
– продолжительность транспортной операции; – продолжительность технологической операции;
– продолжительность технологической операции; – продолжительность цикла установки;
– продолжительность цикла установки; – интервал времени между первыми загрузкой и разгрузкой емкости-накопителя;
– интервал времени между первыми загрузкой и разгрузкой емкости-накопителя; – продолжительность технологического цикла аппарата периодического действия;
– продолжительность технологического цикла аппарата периодического действия; – объем порции продукта, поступающего из подающего аппарата в емкость-накопитель;
– объем порции продукта, поступающего из подающего аппарата в емкость-накопитель; – объем порции реакционной массы, выгружаемой из емкости-накопителя в принимающий аппарат;
– объем порции реакционной массы, выгружаемой из емкости-накопителя в принимающий аппарат; – минимальное и максимальное значение коэффициента заполнения объема аппарата.
– минимальное и максимальное значение коэффициента заполнения объема аппарата.