Параметризация обобщенных обратных матриц: алгоритмическое и программное обеспечение
| Демидов Н.Е. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Во многих приложениях (линейная алгебра, математическая статистика, теория управления, математическое программирование и др.) получили широкое применение различные типы обобщенных обратных (псевдообратных, квазиобратных) матриц (ООМ) [1, 2]. В специальной литературе проблемы использования ООМ связываются обычно с решением систем линейных алгебраических уравнений (СЛАУ) с прямоугольными матрицами неполного строчного или столбцового ранга. Для таких матриц их ООМ в общем случае не единственные и однозначно определяются при наложении дополнительных условий в виде матричных уравнений или ранговых зависимостей [1]. Известные соотношения для получения общего представления ООМ через исходную матрицу и ее конкретную ООМ содержат свободные параметры в виде матриц того же размера, что и у исходной или ее ООМ, то есть являются сверхпараметризованными, что может быть неприемлемым в практических задачах. В настоящее время существует достаточно большое число различных типов ООМ и лишь для некоторых из них, и в первую очередь ООМ Мура–Пенроуза, имеются детально теоретически обоснованные надежные прямые вычислительные алгоритмы и высокоэффективные программные модули, их реализующие. Для некоторых специальных типов ООМ предлагаются алгоритмы [2] с громоздкими математическими выкладками и рекурсивным характером вычислений. В этой связи представляется актуальной разработка комплексов алгоритмического и программного обеспечения, реализующих на единой методологической основе минимальные параметризированные представления ряда известных типов ООМ и эффективные прямые методы их вычисления с поддерживающими модулями, функционирующими в среде системы для математических расчетов MATLAB. Пакет MATLAB фирмы The Mathworks, Inc. (США), занимающий ведущие позиции в качестве стандартного программного средства для высшей школы в развитых странах, обладает достаточными базовыми возможностями для выполнения возникающих при вычислении ООМ таких операций с матрицами, как определение ранга, ортогональные преобразования, разложение по сингулярным числам и других [3]. Основные типы ООМ Пусть А – матрица размера n на m. Примем без потери общности условия n>m и k=rankA AXA=A, (1) XAX=X, (2) AX=(AX)T, (3) XA=(XA)T. (4) Известно, что такая ООМ – единственная. Обозначим ее как {1,2,3,4}–ООМ. Если принять, что условие (1) является обязательным, то параметризованным семейством ООМ Мура–Пенроуза являются ООМ типов {1}, {1,2}, {1,3}, {1,4}, {1,3,4}, {1,2,3}, {1,2,4}. Если заданы положительно определенные обратимые матрицы M порядка n и N порядка m, то существует единственная взвешенная ООМ Мура–Пенроуза, удовлетворяющая, помимо условий (1) и (2), соотношениям MAX=(MAX)T, (5) NXA=(NXA)T. (6) Если ее обозначить как {1,2,5,6}–обратную, то ее параметризованным семейством будут ООМ типов {1}, {1,2}, {1,5}, {1,6}, {1,5,6}, {1,2,5} и {1,2,6}. При n = m определены следующие специальные типы ООМ. Если совместно с условиями (1) и (2) выполняется соотношение AiX=XAi, (7) то единственная матрица X называется слабокоммутирующей ООМ для A и имеет тип {1,2,7}. На параметр i накладывается ранговое условие i >=l, где l – наименьшее положительное целое, такое, что rank Al = rank Al+1. Параметризованным семейством {1,2,7}–ООМ являются ООМ типов {1}, {1,2} и {1,7}. Если i = 1, то имеется ограничение AX=XA. (8) Единственная {1,2,8}–ООМ для A существует тогда и только тогда, когда rank A = rank A2 . Такая ООМ называется групповой обратной (group inverse) и имеет параметризованное семейство ООМ типов {1}, {1,2}, {1,8}. Минимальная параметризация ООМ Предлагаемое решение задачи минимальной параметризации основывается на следующих предположениях. 1. Существуют линейно–алгебраические преобразования матриц A и X, сохраняющие для получаемых матриц B и Y свойства (1) и (2). 2. Матрицы B и Y имеют простейшую структуру, позволяющую задать для Y минимально возможное число свободных параметров. 3. Для базовых типов ООМ ({1,2,3,4}, {1,2,5,6}, {1,2,7} и {1,2,8}) значения всех параметров фиксированы, а для каждого из типов параметризированного семейства фиксируются только значения определенной части свободных параметров ООМ базового типа. 4. Обратное преобразование параметризованной матрицы Y сохраняет для исходной матрицы A и ее параметризованной ООМ их конкретные свойства, задаваемые соответствующими условиями из (3)–(8), если при формировании Y эти свойства учитывались. 5. В связи с использованием только линейно-алгебраических операций свободные параметры входят линейно в записи элементов параметризованного представления ООМ. С помощью преобразования вида B = SAQ = получается матрица простейшего вида B, параметризованная ООМ типа {1} для которой имеет вид Y = где S и Q – невырожденные матрицы порядка n и m соответственно; Ek – единичная матрица порядка k. При P3 = P2P1 матрица Y является {1,2}–ООМ для B, что легко проверить подстановкой выражений для B и Y в условия (1) и (2). Матрица X = QYS обладает по отношению к A = S-1BQ-1 такими же свойствами. Таким образом, получена минимальная параметризация ООМ в виде X = Q Если известна ООМ для A одного из базовых типов, то конкретные значения ее параметров находятся из решения следующей обратной задачи параметризации Y = Q-1XS-1= Для параметризованного семейства с базовым типом {1,2,3,4}–ООМ конкретные ООМ со свободными параметрами задаются следующими соотношениями: {1} – P1 ¹ R1; P2 ¹ R2; P3 ¹ P2P1, {1,2} – P1 ¹ R1; P2 ¹ R2; P3 = P2P1, {1,3} – P1 = R1; P2 ¹ R2; P3 ¹ P2P1, {1,4} – P1 ¹ R1; P2 = R2; P3 ¹ P2P1, {1,2,3} – P1 = R1; P2 ¹ R2; P3 = P2P1, {1,2,4} – P1 ¹ R1; P2 = R2; P3 = P2P1, {1,3,4} – P1 = R1; P2 = R2; P3 ¹ P2P1. Для параметризованных семейств с другими базовыми типами ООМ также могут быть получены подобные соотношения. Специальные параметризации ООМ Во многих практических случаях при операциях с матрицами большого размера могут возникнуть проблемы даже при минимальных параметризациях ООМ. В этом случае предлагается использовать аппроксимирующие параметризации, для которых число свободных параметров либо не зависит от размеров исходных матриц, либо заведомо меньше их максимального размера n. Если для базового типа ООМ имеется решение задачи обратной параметризации, то предлагаемая аппроксимирующая параметризация вида Y = Q-1XS-1 = позволяет с помощью двух диагональных матриц свободных параметров D1 и D2 для {1,2,3,4}–ООМ получить следующие типы слабопараметризованных ООМ: {1,2}, {1,2,3} и {1,2,4}. При D1 = fE и D2 = gE (E – единичные матрицы соответствующих порядков) имеется всего два свободных параметра с тем же семейством параметризованных ООМ. Подобные параметризации позволяют получать структурированные ООМ, содержащие заданные нулевые строки и столбцы, что делает возможным, например, изменять тип и порядок динамических обратных связей (ОС) в линейных дискретных системах путем задания соответствующих значений свободных параметров [4], реализуя программно регуляторы с переменной структурой. Вычисление ООМ и их параметризаций Предложенное единое параметризованное представление рассмотренных выше типов и семейств ООМ позволило разработать общую схему вычисления ООМ с использованием преобразования исходной матрицы A к виду B = SAQ = Для нахождения матриц параметров P1 и P2 в {1,2}–ООМ Y для B Y = в ограничения из (3)–(8), определяющие конкретный базовый тип ООМ, подставляются выражения A = S-1BQ-1 и X = QYS, после чего находятся зависимости для расчета P1 и P2. Рассмотрим пример из [2], для которого n = m = 3, k = 2 и матрицы A, Q и S имеют следующие значения: A= В случае {1,2,3,4}–ООМ для A P1=W11-1W12 и P2=V21V11-1, где W=S-TS-1= P1= В случае {1,2,5,6}–ООМ для A P1=W11-1W12 и P2 = -V22-1V21, где M= W=S-TMS-1= V=QTNQ= P2= [0,5 1], X= В случае {1,2,7}–ООМ для A при A2X=XA2 P1 = W11-1W12 и P2 = W21W11-1, где W=Q-1AS-1= P2=[0,5 -0,5], X= В случае {1,2,8}–ООМ для A при AX = XA P1 = W11-1W12 и P2 = W21W11-1, матрица W = Q-1S-1, а матрицы P1, P2 и X такие же, как у {1,2,7}–ООМ для A. Программное обеспечение для вычисления ООМ и их параметризаций Комплекс программных модулей, реализующих описанные выше операции по вычислению ООМ и их параметризаций, оформлен в виде m-файлов системы для математических расчетов MATLAB [3,4] и расширяет ее стандартные возможности базовыми и вспомогательными алгоритмами для решения нетривиальных задач с ООМ. Ниже приведен текст одного из базовых модулей комплекса, реализующего вычисление взвешенной ООМ Мура–Пенроуза (m–файл gi1256.m): function [P1,P2]=GI1256(k,Q,S,M,N) n=size(S); m=size(Q); S1=inv(S); V =Q'*N*Q; W =S1'*M*S1; W11=W(1:k,1:k); W12=W(1:k,k+1:m); P1=inv(W11)*W12; V22=V(k+1:n,k+1:n); V21=V(k+1:n,1:k); P2=-V21*inv(V22); Пример использования параметризованной ООМ При расчете расширенной динамической ОС в задаче апериодического управления [4] возникает необходимость решения матричного уравнения вида L=KG, где K – матрица расширенной динамической ОС, G и L – блочные матрицы специальной структуры, причем G – полного столбцового ранга. Конкретное уравнение имеет следующий вид [-1 -5 -10 -3 -6] = K Решение K=LG+ (G+ – ООМ для G) не является единственным, что позволяет использовать специальную параметризацию G+ с тремя свободными параметрами a, b и c для вычисления матрицы параметризованной ОС, принимающей при конкретных значениях параметров следующие структурные формы. 1. Динамический компенсатор 2 порядка при a = - K = [-6 -3 8 3 -3 -1 0 -3]. 2. Динамический компенсатор 1 порядка при a = K = [-0,5 -2,5 -0,5 -1 0 0 -0,5 0]. 3. Статическая ОС по выходу при a = 0, b = 0, c = 0, K = [-1 -3 0 0 0 0 0 0]. Список литературы 1. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. – М.: Наука, 1997. – 224 с. 2. Wang Guo – rong, Chen Yong – lin. A recursive algorithm for computing weighed Moore – Penrouse inverse // Journal of Computation Mathematics. – 1986, v. 4. – №1. – P. 74 – 85. 3. Дьяконов В.П. Справочник по применению системы PC MATLAB. - М.: Наука, 1993. –112 c. 4. Демидов Н.Е. Программная система для разработки и исследования модифицированных алгоритмов апериодического управления // Программные продукты и системы. – 1997. – №2. – С. 42 – 45. |
http://swsys.ru/index.php?id=986&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Автоматизированная система принятия решений при стратегическом планировании устойчивого развития региона в условиях нечеткой информации
- Оптимизация обработки информационных запросов в СУБД
- Реализация теней с помощью библиотеки OpenGL
- Сравнение сложных программных систем по критерию функциональной полноты
- Комплекс программных средств для аналитических иерархических процессов экспертного оценивания


 ,
, S.
S. .
.
 .
.
 ,Q=
,Q= ,S=
,S= .
. , V=Q-1Q-T=
, V=Q-1Q-T= ,
, , P2= [0,4 0], X=
, P2= [0,4 0], X= .
. , N=1
, N=1 ,
, ,
, , P1=
, P1= ,
, .
. , P1=
, P1= 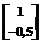 ,
, .
. .
. , b = -
, b = - , c = -
, c = -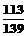 ,
, , b = 0, c = 0,
, b = 0, c = 0,