Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование систем массового обслуживания с абсолютным приоритетом
Аннотация:
Abstract:
| Автор: Русинов И.А. () - | |
| Ключевые слова: системы обслуживания, моделирование, массовое обслуживание, абсолютный приоритет |
|
| Keywords: , modeling, , |
|
| Количество просмотров: 24104 |
Версия для печати Выпуск в формате PDF (2.59Мб) |
В реальных условиях функционирования систем массового обслуживания (СМО) достаточно часто возникают ситуации, когда обслуживание отдельных судов должно производиться вне всякой очереди, если только в очереди нет заявок, имеющих такие же преимущества. В этом случае рассматривается несколько групп заявок, причем заявки первой группы (первого приоритета, первого ранга) имеют преимущество над заявками второй группы, а те, в свою очередь, над заявками третьей группы, и так далее.
Возникающие при этом способы обслуживания нескольких потоков, соответствующих группам заявок с различными приоритетами, могут быть решены по-разному. Достаточно часто рассматривают системы с абсолютным приоритетом. Если заявка с абсолютным приоритетом застает все каналы занятыми, то обслуживание одной из заявок с низшим приоритетом прекращается, а на освободившемся канале осуществляется обработка заявки с высшим приоритетом. После того как обработка судна с высшим приоритетом заканчивается, а других заявок с высшим приоритетом в очереди нет, возобновляется прерванное обслуживание заявки с низшим приоритетом. В настоящей работе автором предлагается метод результирующих средних, который позволяет определять среднее время ожидания нескольких групп заявок с различными приоритетами как для одноканальных, так и для многоканальных СМО. Сформулируем задачу для одноканальной системы. Пусть на вход СМО может поступать L групп заявок, причем входной поток каждой группы представляет собой простейший поток с интенсивностью ll (l=1,2..L). Тогда суммарный входной поток всех групп заявок также будет простейшим с интенсивностью 1. Результирующее среднее время ожидания первых р групп заявок зависит только от суммы интенсивностей соответствующих потоков 2. Результирующее среднее время ожидания групп заявок с приоритетом больше р(l=р+1, р+2,..L) и среднее время ожидания р+l-й группы судов зависит только от суммарной интенсивности заявок с более высокими приоритетами, меньше и не зависит от соотношений между интенсивностями этих потоков. Это допущение вытекает из положения о независимости результирующего среднего времени ожидания от дисциплины обработки грузов. Рассмотрим плотности отдельных потоков
где t(p) – результирующее среднее время ожидания групп заявок с первыми р приоритетами. Исходя из второго допущения, можно записать следующее равенство:
Выражение (2) представляет собой математическое ожидание результирующего времени ожидания первых p групп заявок, полученное на основе байесова подхода. Тогда среднее время ожидания для заявок с p-м приоритетом определяется из (2) на основе рекуррентного выражения вида:
При этом для p=1 Подставив в выражение (3) выражение (2), получим следующее выражение для результирующей средней времени ожидания:
Метод результирующих средних может быть использован и для многоканальных СМО. При этом следует сделать дополнительное допущение о том, что обработка судов с различным приоритетом осуществляется с одинаковой интенсивностью. Для систем без взаимопомощи эта интенсивность равна m, а в системах с частичной взаимопомощью предполагается, что интенсивность обработки всех заявок независимо от приоритета примерно одинакова. Тогда для определения среднего времени ожидания можно (как в одноканальной системе) воспользоваться выражением (4). При этом результирующее среднее время ожидания для p групп судов (l=1,2,..p) будет определяться выражениями:
где Р0 – вероятность того, что все каналы свободны; ri – коэффициент интенсивности обслуживания заявки в i-м состоянии; S – число каналов; rs – максимальная интенсивность обслуживания заявок при n≥S. Указанные модели были использованы при решении задач исследования и оптимизации процессов обработки судов на контейнерных терминалах. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1599 |
Версия для печати Выпуск в формате PDF (2.59Мб) |
| Статья опубликована в выпуске журнала № 3 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Моделирование управляемых многоканальных систем массового обслуживания
- Алгоритм и программа расчета напряженно-деформированного состояния песчаных грунтов при циклическом нагружении
- Моделирование информационных процессов систем управления большими данными для решения задач кибербезопасности
- Информационно-вычислительная система моделированияи прогнозирования торфяных пожаров
- Моделирование оптимальных условий биосинтеза
Назад, к списку статей



 . Здесь и далее значение l соответствует номеру приоритета. Интенсивность обслуживания всех заявок одинакова и равна m. При определении времени ожидания различных заявок сделаем два допущения.
. Здесь и далее значение l соответствует номеру приоритета. Интенсивность обслуживания всех заявок одинакова и равна m. При определении времени ожидания различных заявок сделаем два допущения.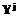 и не зависит от интенсивности потоков с более низким приоритетом ll (l=р+1, р+2,..L). Это допущение вытекает из определения абсолютного приоритета.
и не зависит от интенсивности потоков с более низким приоритетом ll (l=р+1, р+2,..L). Это допущение вытекает из определения абсолютного приоритета. и суммарных потоков
и суммарных потоков 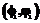 . В соответствии с первым допущением результирующее среднее время ожидания группы заявок с первым приоритетом, групп заявок с первым и вторым приоритетами и групп заявок с р приоритетами запишем:
. В соответствии с первым допущением результирующее среднее время ожидания группы заявок с первым приоритетом, групп заявок с первым и вторым приоритетами и групп заявок с р приоритетами запишем: ;
;  ;
;  ,(1)
,(1) . (2)
. (2) . (3)
. (3) .
.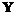 . (4)
. (4) ; (5)
; (5) , (6)
, (6)