Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Модель и алгоритмы интерактивного оценивания знаний
Аннотация:Рассматриваются задачи тестирования и оценивания знаний, которые сводятся к решению вопросов оценки качества тестового материала, определения алгоритмов тестирования, сценариев обучения и методов оценивания знаний путем тестирования. На основе перечисленных компонент разработана интерактивная модель оценивания знаний, которая доведена до уровня алгоритмов.
Abstract:Considered testing and knowledge estimating problems are solved by estimating of test material quality, definition of testing algorithms, definition of testing scenarios and definition of knowledge estimating testing methods. There were developed an interactive knowledge estimating model, presented as a set of algorithms. It’s based on based on components that were indicated previously.
| Авторы: Александрова Л.А. (tumbinskaya@inbox.ru) - Казанский государственный технический университет им. А.Н. Туполева, кандидат технических наук, Тумбинская М.В. (tumbinskaya@inbox.ru) - Казанский национальный исследовательский технический университет (доцент), Казань, Россия, кандидат технических наук | |
| Ключевые слова: интерактивная модель, метод оценивания, сценарий обучения, тестирование |
|
| Keywords: interactive model, estimating method, teaching scenario, testing |
|
| Количество просмотров: 12768 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
В настоящее время достаточно интенсивно разрабатываются и используются разнообразные системы тестирования, которые представляют собой как отдельные самостоятельные программные продукты, так и модули, встроенные в обучающие системы. Применение интерактивных обучающих систем позволяет индивидуализировать процесс обучения, обеспечить самоконтроль и централизованный контроль знаний обучаемого с диагностикой ошибок и обратной связью с процессом управления знаниями. Под интерактивностью в статье понимается способность обучающей системы активно взаимодействовать с обучаемым и преподавателем. В данной статье предлагаются модель и алгоритмы интерактивного оценивания знаний, которые позволят любому преподавателю с минимальными усилиями создавать качественные тестовые задания, дифференцированно оценивать знания, определять сценарий обучения, повышать качество учебного процесса. В работе [1] предложена функциональная модель
где K – множество компонент обучающей системы; Pf – набор процедур для формирования компонент; N – множество параметров, определяющих интерактивную обучающую систему; Y – оценка полученного знания. В модели используются 10 компонент: компонента исследования, принятия решения, формирования контента, компонента интерактивности, обучения, компонента оценивания, контроля, компонента формирования теоретического материала, тестового материала, сценариев обучения. Под компонентой понимаются модель, подсистема, программа. Анализ литературных источников показывает, что практически не уделяется внимание компоненте интерактивности. Тема оценивания знаний активно дискутируется, но до настоящего времени нет обобщенной интерактивной модели оценивания, которая затрагивает вопросы оценивания качества тестирующего материала, оценивания тестовых заданий (ТЗ), определения их весовых коэффициентов, организации процесса тестирования, выбора метода оценивания знаний и выработки рекомендаций по дальнейшему обучению. Данная статья посвящена компоненте оценивания. Модель компоненты оценивания Предлагаемая модель компоненты оценивания Kоц представлена соотношением Kоц =áX, M, Pz, Rp, Yñ, (2) где X – множество тестовых материалов; M – оценка тестового материала на основе показателей качества тестовых заданий Предложенная модель является интерактивной. Таким образом, разработка компоненты оценивания предполагает выполнение следующих шагов: подготовку тестового материала и базы сценариев тестирования, разработку алгоритма определения весовых коэффициентов ТЗ и обобщенного алгоритма интерактивного оценивания знаний, а также определение управляющих воздействий по дальнейшему процессу обучения. Подготовка тестового материала преподавателем-предметником выполняется в соответствии с методологическими требованиями к программно-дидактическим тестам, ТЗ и технологиям компьютерного тестирования [2]. На первом шаге определяются показатели оценивания ТЗ, заложенные в основу решающих правил для классификации их на допустимые (корректные), недопустимые ТЗ и требующие индивидуального рассмотрения. Правила могут быть сформированы как экспертом, так и с помощью алгоритмов формирования решающих правил по обучающим выборкам. Процедура оценки корректности ТЗ сводится к следующим шагам. 1. Преподаватель-предметник подготавливает множество ТЗ: 2. Определяется множество показателей p, по которым будут оцениваться ТЗ, 3. Определяетcя значение показателей 4. На основе требований и с учетом введенных показателей формируются решающие правила: РП1 – решающее правило отнесения ТЗ к классу допустимых ТЗ; РП2 – решающее правило отнесения ТЗ к классу недопустимых ТЗ. 5. С помощью решающих правил РП1, РП2, множество ТЗ {X} разбивается на классы Решающее правило РПj строится в виде суперпозиции решающих функций:
где s1 – количество решающих правил, описывающих класс допустимых, а s2 – недопустимых ТЗ. В общем виде решающее правило
где 6. По результатам классификации эксперт модифицирует, совершенствует решающие правила, в некоторых случаях пересматривает параметры 7. Формируется множество ТЗ: Подготовка базы сценариев тестирования. Сценарий тестирования определяется следующими параметрами: способ представления выборки ТЗ; процедура выбора ТЗ; ограничение на время тестирования; сложность ТЗ, предъявляемых в начале тестирования; процесс изменения сложности предъявляемых ТЗ; зависимость выбираемого ТЗ от ответа обучаемого; процесс ответа на ТЗ; возврат к обучающему материалу; повторное тестирование; ограничение на количество попыток тестирования (только для самообучения); требование ввода ответа на все ТЗ; вывод результатов тестирования; требование вывода неверных ответов (только для самообучения); требование вывода рекомендаций по изучению теоретического материала; требование вывода правильных ответов (только для самообучения); возможность просмотра обучающего материала во время тестирования (только для самообучения); возможность подсказки при неправильном ответе на ТЗ (только для самообучения); объем базы ТЗ. На основе параметров можно сформировать следующий обобщенный алгоритм сценария тестирования. 1. Определить значения всех параметров. 2. Сформировать выборку из ТЗ длины h. 3. Определить способ выбора ТЗ из экзаменационной выборки. 4. В случае преднамеренного способа выбора все ТЗ экзаменационной выборки упорядочить по степени сложности. 5. Выбрать способ представления выборки ТЗ (для оценивания целесообразно предъявлять ТЗ по одному элементу, для самоаттестации это не имеет значения). 6. Задать (отменить) ограничение на время тестирования. 7. Случайный способ выбора ТЗ реализовать с помощью генератора случайных чисел, а для преднамеренного способа выбора ТЗ необходимо определить сценарий их предъявления: от простого ТЗ к ТЗ средней сложности, а затем к сложному; от ТЗ средней сложности к сложному; от ТЗ средней сложности к простому. Переход от одного уровня сложности к другому (на более высокий или более низкий) выполняется в зависимости от ответа на предыдущее ТЗ. 8. Определить правила ввода ответов на ТЗ: последовательно, в порядке их поступления или произвольно. 9. Разрешить обучаемому вернуться к обучающему материалу, получить подсказку при неправильном ответе. Данные действия возможны только при самоаттестации. 10. Разрешить повторное тестирование при оценивании знаний. При самоконтроле запрещать повторное тестирование нецелесообразно. 11. Разрешить вернуться к обучающему материалу перед повторным тестированием. 12. Задать требование ввода ответа на все ТЗ экзаменационной выборки. 13. Определить параметры вывода результатов тестирования: вывод количества неверных ответов, вывод номера или содержания ТЗ, на которые получены неверные ответы, вывод рекомендаций по дальнейшему обучению, вывод правильных ответов. Алгоритм определения весовых коэффициентов ТЗ приписывает вес тестовым заданиям, который будет использоваться при оценивании знаний. 1. Каждое тестовое задание xiÎX оценивается преподавателем-экспертом по степени сложности: простое, сложное, средней сложности. Таким образом, исходное множество X разбивается на классы 2. Элементы каждого класса 3. Упорядоченные ТЗ ранжируются: каждому элементу xi класса
где di – ранг i-го элемента в классе 4. Определяется весовой коэффициент wi ТЗ xi, Процедуру упорядочения рассмотрим на примере одного класса 1. Выбирается пара ТЗ 2. Тестовые задания xq и xp оцениваются по сложности, то есть между ними устанавливается одно из соотношений: xq > xp, xq < xp, xq ~ xp (6) (знак > означает превосходство одного ТЗ над другим по степени сложности). 3. Выбирается следующий элемент xr из класса 4. Определяется местонахождение следующего элемента xi класса 5. Процесс упорядочения происходит до тех пор, пока все элементы класса Обобщенный алгоритм интерактивного оценивания знаний разрабатывается следующим образом. 1. Каждому тестовому заданию xi ставится в соответствие набор значений параметров - параметр p1 характеризует правильность ответа на ТЗ:
- p2 – вес тестового задания; - P3 – суммарное время ответа на ТЗ. На параметр p3 накладывается ограничение, по достижении которого тестирование прекращается и выставляется итоговая оценка. 2. Итоговая оценка
4. При аттестации по балльно-рейтинговой системе оценка
где 5. Традиционная оценка выставляется в соответствии с соотношением:
где граничные значения yотл, yхор, yудовл определяются экспертным путем (в Казанском государственном техническом университете им. А.Н. Туполева приняты следующие значения: yотл=86, yхор=71, yудовл=51). Определение управляющих воздействий по дальнейшему обучению осуществляется в соответствии с решающими правилами Rp, сформированными экспертным путем: rp1 – допустить к итоговой аттестации; rp2 – пройти повторное обучение; rp3 – признать итоговую оценку знаний; rp4 – провести дополнительное оценивание знаний; rp5 – сформировать новый контент. В заключение следует отметить, что предложенная модель и алгоритмы интерактивного оценивания знаний, используемые при создании интерактивных обучающих систем, позволяют создавать качественные тестовые задания, выставлять оценку знаний с учетом сложности ТЗ, адаптировать процесс обучения под обучаемого и преподавателя, создавать интеллектуальные интерактивные обучающие системы, повышать качество обучения. Литература 1. Александрова Л.А., Тумбинская М.В. Модель интерактивной обучающей системы // Программные продукты и системы. 2009. № 2. С. 175–178. 2. Васильев В.И., Киринюк А.А., Тягунова Т.Н. Требования к программно-дидактическим тестовым материалам и технологиям компьютерного тестирования. М.: Изд-во МГУП, 2005. 27 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2316 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
| Статья опубликована в выпуске журнала № 3 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программа для автоматизированной верификации ограничений целостности баз данных
- Подход к развитию системы управления тестированием программных средств
- Особенности применения предметно-ориентированных языков для тестирования веб-приложений
- Способы инициализации многопроцессорной системы
- Оптимизация периодичности инициализации контроля на основе дублированных вычислений
Назад, к списку статей



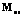 интерактивной обучающей системы, разработанная на основе компонентного подхода:
интерактивной обучающей системы, разработанная на основе компонентного подхода: , (1)
, (1) ; Pz – процедура оценивания знаний;
; Pz – процедура оценивания знаний; 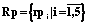 – решения преподавателя; Y – результат оценивания знаний, Y=(y1, y2), где y1 – традиционная оценка, y2 – балльно-рейтинговая оценка.
– решения преподавателя; Y – результат оценивания знаний, Y=(y1, y2), где y1 – традиционная оценка, y2 – балльно-рейтинговая оценка. .
. . Наиболее распространенными показателями ТЗ являются форма, сложность формы ТЗ, синтаксическая грамотность вопроса, ответа, соответствие ТЗ предметной области, вероятность угадывания правильного ответа и др.
. Наиболее распространенными показателями ТЗ являются форма, сложность формы ТЗ, синтаксическая грамотность вопроса, ответа, соответствие ТЗ предметной области, вероятность угадывания правильного ответа и др. . Каждое ТЗ xi описывается вектором
. Каждое ТЗ xi описывается вектором 
 ,
,  ,
,  .
. ,
,  ,
,  : класс допустимых, недопустимых и класс промежуточных значений, соответственно. Класс
: класс допустимых, недопустимых и класс промежуточных значений, соответственно. Класс  .
. (3)
(3) имеет вид дизъюнктивно-конъюнктивной фор- мы:
имеет вид дизъюнктивно-конъюнктивной фор- мы: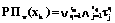 ,
,  , (4)
, (4) – критерий корректности ТЗ, сформированный на основе параметров
– критерий корректности ТЗ, сформированный на основе параметров  исключаются из множества X и выдаются рекомендации по их модификации,
исключаются из множества X и выдаются рекомендации по их модификации,  включаются (исключаются) в исходное множество X по усмотрению эксперта.
включаются (исключаются) в исходное множество X по усмотрению эксперта. . В дальнейшем классы
. В дальнейшем классы 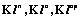 будем называть классами простых, сложных ТЗ и ТЗ средней сложности.
будем называть классами простых, сложных ТЗ и ТЗ средней сложности. ,
, 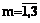 , присваивается свой ранг di, определяемый по формуле
, присваивается свой ранг di, определяемый по формуле , (5)
, (5) ,
,  ,
,  ,
,  , d0=0,
, d0=0,  ; D – шаг приращения; n – количество градаций в классе
; D – шаг приращения; n – количество градаций в классе 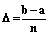 , где a, b – минимальная и максимальная градации в классе
, где a, b – минимальная и максимальная градации в классе  , где
, где  – весовой коэффициент класса ТЗ, заданный экспертом.
– весовой коэффициент класса ТЗ, заданный экспертом. .
. между выбранными элементами,
между выбранными элементами,  ,
,  . Отметим, что может возникнуть такая ситуация, когда
. Отметим, что может возникнуть такая ситуация, когда  или
или  (при сравнении рассматриваются эквивалентные ТЗ). В этих случаях xp и xr или xq и xr будут иметь одинаковый ранг.
(при сравнении рассматриваются эквивалентные ТЗ). В этих случаях xp и xr или xq и xr будут иметь одинаковый ранг. , где
, где  .
. :
:
 вычисляется по формуле:
вычисляется по формуле: . (7)
. (7) , отведенных на данный тест (аттестацию):
, отведенных на данный тест (аттестацию): , (8)
, (8)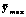 – количество баллов, за которые эксперт выставляет наивысшую оценку.
– количество баллов, за которые эксперт выставляет наивысшую оценку. , (9)
, (9)