Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Система вычисления приоритетов на основе матриц парных сравнений
Аннотация:отбор, упорядочение, классификация, модель выбора, методы выбора, критерий, важность критерия, функция полезности, функция принадлежности, конфигурация системы.
Abstract:The system is composed of a software system SVIR-R as a dynamic link library. It is intended to form the matrix of paired comparisons, analysis of their consistency and calculating the priorities of the entity. Algorithm for calculating the priorities is invariant under the four types of matrices, implemented in the system. The method of analysis of hierarchies is realized in it together with the system SVIR-R formed on the model of choice in it
| Авторы: Микони С.В. (svm@sm4265.spb.edu) - Петербургский государственный университет путей сообщения, доктор технических наук, Киселёв И.С. (svm@sm4265.spb.edu) - Петербургский государственный университет путей сообщения | |
| Ключевые слова: многокритериальная оптимизация, согласованность предпочтений, приоритет сущности, экспертное предпочтение, матрица парных сравнений |
|
| Keywords: multicriteria optimization, the consistency of preferences, entity priority, expert preference, matrix of paired comparisons |
|
| Количество просмотров: 20183 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
Усилиями американского математика Томаса Саати метод анализа иерархий (МАИ) получил широкое распространение [1]. Он имеет многочисленные программные реализации. Метод основан на использовании матриц парных сравнений (МПС), содержащих кратные предпочтения. Под кратным предпочтением aкпij понимается превосходство i-й сущности xi над j-й сущностью xj, xi, xjÎX в k раз, kÎ[0,1; 10]. Однако, кроме использования в МАИ, МПС имеют самостоятельную ценность. Они могут использоваться в задачах распределения ресурсов, расчета приоритета сущностей, вычисления весовых коэффициентов для обобщающих функций в задачах скалярной оптимизации [2], а также отражать и другие типы предпочтений – ординальные (факты предпочтений), вероятностные предпочтения (в долях от 1), соотношения выигрышей и потерь. Помимо субъективных (экспертных) предпочтений, МПС могут отражать объективные предпочтения, такие как результаты футбольного первенства или товарообмен между хозяйствующими субъектами. Таким образом, в качестве объекта программной реализации целесообразно использовать не метод анализа иерархий, а его важнейшее звено – МПС как более универсальную модель. Этот принцип реализован в программной системе, названной системой вычисления приоритетов (СВП). В статье излагаются возможности этой системы. Создание МПС Программная система СВП реализована в виде динамической библиотеки системы выбора и ранжирования СВИРЬ-Р. Из системы СВИРЬ-Р задаются перечень сопоставляемых сущностей, размерность и тип матрицы. В саму систему возвращается вектор нормированных приоритетов, сформированный на основе МПС. Тип МПС (кратности предпочтений, фактов предпочтений, долей от 1 или отношения «Выигрыши/Потери») может задаваться также и внутри системы СВП.
Ручное задание и редактирование предпочтений осуществляются на правой стороне вкладки. В верхней ее части фиксируются имена сопоставляемых сущностей. Каждому типу матрицы соответствуют три ряда окошек ввода. При вводе предпочтения в выбранное окошко его значение пересчитывается в окошках других типов матриц. Универсальным способом ввода является использование движка на биполярной шкале. Ввод единицы и нуля в матрицу фактов предпочтений осуществляется отклонением движка вправо/влево от точки «Равноценны». За исключением МПС «Выигрыши/Потери», остальные типы матриц симметричны относительно главной диагонали. Это позволяет заполнять клетки только одной треугольной подматрицы. Значения (N(N–1)/2) клеток симметричной треугольной подматрицы вычисляются на основе свойства симметрии. При формировании МПС большой размерности эксперты испытывают трудности в нахождении предпочтений для всех пар сущностей. Поскольку в таких случаях некоторые клетки матрицы оказываются пустыми, возникает проблема их заполнения. Она может решаться как формированием подсказок экспертам, так и путем автоматического вычисления предпочтений. Для реализации обоих способов требуется дополнительная информация. В качестве таковой логично использовать условие неухудшениясогласованности предпочтений, присущих исходной матрице. Наиболее очевидным является соблюдение условия порядковой согласованности МПС, заключающееся в обеспечении транзитивности предпочтений. Оно напрямую реализуется для МПС фактов предпочтений в процессе построения замыкающей дуги aik относительно уже введенных предпочтений aij и ajk. Элемент aik МПС служит подсказкой для ввода последующих предпочтений, что исключает возможную противоречивость предпочтений (возникновение циклов в графе). Минимальное число предпочтений, необходимое для построения транзитивного замыкания графа, определяется гамильтоновой цепью, включающей все сопоставляемые сущности (вершины графа доминирования). Поскольку гамильтонова цепь связывает N вершин графа N–1 дугами, минимизация ввода предпочтений достигается путем выбора только тех пар, в которых одна из сущностей не встречалась в предыдущих парах. Например, семью сравнениями вместо N(N–1)/2=28 можно ограничиться при формировании матрицы размерностью 8´8. Для матриц с количественными предпочтениями недостаточно построить транзитивное замыкание графа доминирования. Необходимо определить способ нахождения количественных оценок предпочтений. Он основан на нахождении таких чисел в пустых клетках матрицы, которые доставляют максимум функции согласованности. Максимум достигается при lmax®n, где lmax – максимальное собственное число матрицы, n – ее размерность [3]. Анализ свойств МПС выполняется на вкладке «Результат» (рис. 3).
Поскольку матрица на рисунке 2 построена на основе вектора приоритетов (рис. 1), она полностью согласована, что указывает на отсутствие циклов в графе предпочтений, полученном для этой матрицы (см. рис. 3). При необходимости выводится граф предпочтений. Его дуги в отсутствие циклов окрашены в черный цвет. С увеличением числа проходящих через них циклов предпочтений они розовеют. При наведении мыши на дугу приводится список проходящих через нее циклов. Показатель выраженности предпочтений отражает степень несимметричности элементов относительно главной диагонали. Для матрицы кратности предпочтений вычисляется коэффициент количественной (кардинальной) согласованности по формуле, предложенной Т. Саати. В правой части вкладки «Результат» задаются параметры вычисления приоритетов сущностей и результаты вычислений, представленные в абсолютной и порядковой шкалах. Приоритеты сущностей вычисляются на основе матрицы А по итерационной формуле: w=(с×А + Е)k×eт, где E – единичная матрица с элементами eii=1; eт – транспонированный вектор текущих приоритетов с единичными начальными значениями.
СВП может использоваться для многокритериальной оптимизации по методу Саати. Участвующие в оптимизации МПС формируются как экспертами, так и автоматически, по значениям признаков из таблицы системы СВИРЬ-Р. Формирование МПС на основании столбца таблицы осуществляется попарным сравнением его значений. В этом режиме из системы СВИРЬ-Р задаются не только список сущностей и тип МПС для каждого признака, но и параметры вычисления приоритетов c и k. Указывается также способ формирования МПС. Многокритериальная оценка приоритета сущностей вычисляется перемножением матрицы приоритетов сущностей по каждому из критериев на вектор важности этих критериев. Он задается из системы СВИРЬ-Р либо вычисляется на основе экспертных предпочтений в системе СВП. МАИ реализуется путем вычисления приоритетов в таблицах иерархии от листовых до корневой. Результаты однокритериальной и многокритериальной оптимизации возвращаются в таблицы «Решение» системы СВИРЬ-Р. Содержимое МПС с оценками их согласованности и выраженности предпочтений, а также приоритеты сущностей экспортируются в табличный процессор MS Excel для документирования и последующей обработки. Литература 1. Саати Т.Л. Принятие решений при зависимостях и обратных связях. М.: Изд-во ЛКИ, 2007. 357 с. 2. Микони С.В. Многокритериальный выбор на конечном множестве альтернатив: учеб. пособие. СПб: Лань, 2009. 273 с. 3. Микони С.В., Киселев И.С. Приближенный метод доопределения матрицы парных сравнений с кратными предпочтениями // IEEE AIS’07; CAD-2007: тр. конф. (Дивноморское, 3–9 сентября 2007 г.). М.: Наука. Физматлит, 2007. Т. 1. С. 330–335. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2357 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программный комплекс формирования многокомпонентных экспертиз
- Формирование барьера безопасности на космическом аппарате при угрозе воздействия космического мусора методами нечеткой логики
- Интеллектуально-экспертный метод определения оптимального маршрута транспортировки продукции
- Математическая постановка многокритериальной задачи оптимизации плана полета
- Коэволюционный подход к проектированию аналоговых микросхем
Назад, к списку статей



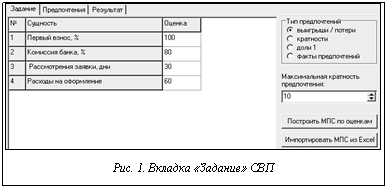 Содержимое МПС может вводиться напрямую экспертами через клавиатуру либо из табличного процессора Excel, содержащего известные предпочтения – экспертные или объективные. Матрица может формироваться автоматически на основе вектора приоритетов, заданного в интервальной шкале. Такая матрица имеет стопроцентную согласованность и в случае количественных предпочтений называется сверхтранзитивной. Пример задания вектора приоритетов (в процентах) для четырех признаков приведен на рисунке 1. В правой части вкладки «Задание» выбираются тип МПС, максимальная кратность предпочтения (по умолчанию 10), а также способ автоматического формирования содержимого матрицы.
Содержимое МПС может вводиться напрямую экспертами через клавиатуру либо из табличного процессора Excel, содержащего известные предпочтения – экспертные или объективные. Матрица может формироваться автоматически на основе вектора приоритетов, заданного в интервальной шкале. Такая матрица имеет стопроцентную согласованность и в случае количественных предпочтений называется сверхтранзитивной. Пример задания вектора приоритетов (в процентах) для четырех признаков приведен на рисунке 1. В правой части вкладки «Задание» выбираются тип МПС, максимальная кратность предпочтения (по умолчанию 10), а также способ автоматического формирования содержимого матрицы. Содержимое МПС, полученное вручную или автоматически, фиксируется на вкладке «Предпочтения» (рис. 2).
Содержимое МПС, полученное вручную или автоматически, фиксируется на вкладке «Предпочтения» (рис. 2).
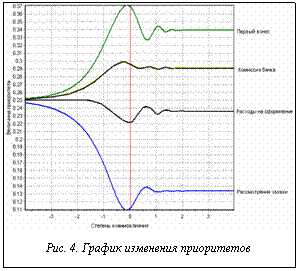 Регулируемые параметры c и k представляют собой масштабный коэффициент (c³1) и степень матрицы. Увеличение масштабного коэффициента улучшает различимость приоритетов, а при k®¥ величина приоритетов учитывает результаты взаимодействия сущностей между собой, то есть их силу. Изменение приоритетов сущностей в зависимости от значения степени k, измеренной в логарифмической шкале, иллюстрируется графиком (рис. 4).
Регулируемые параметры c и k представляют собой масштабный коэффициент (c³1) и степень матрицы. Увеличение масштабного коэффициента улучшает различимость приоритетов, а при k®¥ величина приоритетов учитывает результаты взаимодействия сущностей между собой, то есть их силу. Изменение приоритетов сущностей в зависимости от значения степени k, измеренной в логарифмической шкале, иллюстрируется графиком (рис. 4).